8 800 707 6729
8 800 707 6729Telegram канал

Лицей «Вторая школа» из 5 в 6 класс 2023 год вариант 1

Школа:
Сложность:
Дата экзамена: 03.2023
Печать
youit.school ©

ЛИЦЕЙ ВТОРАЯ ШКОЛА


2023 год


26.03.2023



  1. 8 пирожков и 16 пряников стоят 180 руб. Сколько рублей стоят 6 пирожков и 12 пряников?
  2. Какое наименьшее число воскресений может быть в году?
  3. Автомобиль ехал со скоростью 60 км/ч. Затем он увеличил скорость и стал проезжать каждые 100 м на 1 секунду быстрее, чем в начале. С какой скоростью он стал ехать? Ответ дайте в км/ч.
  4. В классе у Коли столько же учеников, сколько в классе у Оли. Коля говорит Оле: у нас в классе мальчиков вдвое больше, чем у тебя. А Оля отвечает: у нас девочек втрое больше, чем у тебя. Сколько процентов мальчиков в классе у Коли?
  5. Волк бежит за Зайцем. Когда Заяц пробегал мимо почты, Волк находился от него на расстоянии 240 м, а когда Волк добежал до почты, то ему оставалось догнать Зайца 200 м. На каком расстоянии от почты Волк догнал Зайца?
  6. Диагональ делит четырёхугольник с периметром 33 см на два треугольника с периметрами 21 и 30 см. Найдите длину диагонали.
  7. Мотоциклист стартовал от столба 130 км на шоссе, а поезд дошёл до столба 400 км и развернулся в поезд обратно. Он остановился у столба 280 км. Возле какого столба он находился, когда проехал половину своего пути?
  8. Какие значения может принимать выражение (КОТ + ТИР) : (ТОР + КИТ)? Разные буквы — это разные цифры.
  9. С полудня до полуночи Учёный Кот спит под дубом, а с полуночи до полудня он рассказывает сказки. Табличка на дубе говорит: «Два часа назад Кот начал не то, что он будет делать через час». Сколько часов в сутки табличка говорит правду?
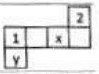
  10. На игральном кубике сумма чисел на противоположных гранях равна 7. Дана развёртка кубика с двумя известными гранями. Найдите сумму чисел на гранях, отмеченных вопросами.
  11. Илья Муромец, Добрыня Никитич и Алёша Попович вступили в бой с великанами. Все богатыри получили по 7 ударов. Илья получил на 7 меньше, чем Добрыня, и на 10 больше, чем Алёша. Сколько всего великанов обороняло их втроём?
  12. Компьютер каждую секунду выполняет две операции: умножает число на 17, затем из результата вычитает 64. С полученным числом он снова делает те же операции. При каком числе на входе, чтобы через 5 секунд на выходе получить 0?
  13. Мама на 18 лет старше Алисы. Когда Алисе было 5 лет, мама была в 3 раза старше. Сколько лет Тане сейчас, если она на 4 года младше Алисы?
  14. Спортсмен пробежал 400 м по кругу и остановился. В точках круга A и B звуковой сигнал звучит каждые 3 минуты отдельно. За какое время оба сигнала совпадут в 5-й раз?
  15. У Печкина волосы растут равномерно, каждый волос живёт полгода. Каждый день выпадает 1 волос. Сколько всего волос на голове у Печкина?
  16. Есть 6 карточек с цифрами 1, 2, 3, 4, 5, 6. Из них можно составить все трёхзначные числа без повторения цифр. Какое наименьшее трёхзначное число получится, если оно делится на 6?
  17. Саша старше Пети на 4 года, а младше Вани на 3 года. Ване 10 лет. Сколько лет Пете?
  18. На дереве сидят 100 воробьёв. Охотник выстрелил и убил одного. Сколько осталось сидеть воробьёв?
  19. Стекло толщиной 1 см и плотностью 2,5 г/см³. Какой вес стекла толщиной 1 см и площадью 20 дм²?
  20. Когда контрольная начинается в 14:45 и длится 1 час 20 минут, во сколько она закончится?
Материалы школы Юайти
youit.school ©

Решения задач



  1. 8 пирожков и 16 пряников стоят 180 руб. Сколько рублей стоят 6 пирожков и 12 пряников?
    Решение: Заметим, что 6 пирожков и 12 пряников составляют $\frac{6}{8} = \frac{3}{4}$ от исходного количества. Тогда стоимость будет равна $\frac{3}{4} \cdot 180 = 135$ руб.
    Ответ: 135.
  2. Какое наименьшее число воскресений может быть в году?
    Решение: В невисокосном году 365 дней, что составляет 52 недели и 1 день. Если год начинается с понедельника, воскресений будет 52. В високосном году 366 дней (52 недели и 2 дня), минимальное число воскресений также 52.
    Ответ: 52.
  3. Автомобиль ехал со скоростью 60 км/ч. Затем он увеличил скорость и стал проезжать каждые 100 м на 1 секунду быстрее. С какой скоростью он стал ехать?
    Решение: Изначальное время прохождения 100 м: $\frac{100}{60 \cdot \frac{1000}{3600}} = 6$ с. Новое время: $6 - 1 = 5$ с. Скорость: $\frac{100}{5} = 20$ м/с = 72 км/ч.
    Ответ: 72.
  4. В классе у Коли мальчиков вдвое больше, чем у Оли, а девочек у Оли втрое больше, чем у Коли. Сколько процентов мальчиков в классе у Коли?
    Решение: Пусть в классе Коли $2m$ мальчиков и $d$ девочек, у Оли $m$ мальчиков и $3d$ девочек. Всего учеников: $2m + d = m + 3d \Rightarrow m = 2d$. Процент мальчиков у Коли: $\frac{2m}{2m + d} = \frac{4d}{5d} = 80\%$.
    Ответ: 80\%.
  5. Волк бежал за Зайцем. Когда Заяц был у почты, Волк находился в 240 м. Когда Волк достиг почты, Заяц был в 200 м. На каком расстоянии от почты Волк догнал Зайца?
    Решение: Пусть скорость Волка $v$, Зайца $u$. Время движения Волка до почты: $\frac{240}{v}$. За это время Заяц пробежал $240 - 200 = 40$ м: $u = \frac{40v}{240} = \frac{v}{6}$. Время догона: $\frac{200}{v - u} = \frac{200}{\frac{5v}{6}} = \frac{240}{v}$. Путь Волка: $v \cdot \frac{240}{v} = 240$ м. Заяц пробежал: $u \cdot \frac{240}{v} = 40$ м. Место встречи: $240 - 40 = 200$ м от почты.
    Ответ: 200 м.
  6. Диагональ четырёхугольника с периметром 33 см делит его на треугольники с периметрами 21 см и 30 см. Найдите длину диагонали.
    Решение: Сумма периметров треугольников: $21 + 30 = 51$ см. Периметр четырёхугольника: $33$ см. Диагональ: $\frac{51 - 33}{2} = 9$ см.
    Ответ: 9 см.
  7. Мотоциклист стартовал от столба 130 км. Поезд дошёл до столба 400 км и развернулся, остановившись у столба 280 км. Где был поезд, когда проехал половину пути?
    Решение: Весь путь поезда: $400 - 280 = 120$ км. Половина пути: $60$ км. От точки разворота: $400 - 60 = 340$ км.
    Ответ: 340 км.
  8. Значение выражения (КОТ + ТИР) : (ТОР + КИТ) может быть равно 1. Например: 123 + 456 = 579; 457 + 167 = 624; $\frac{579}{624} \approx 0,928$. Минимальное значение зависит от подбора цифр.
    Ответ: Возможные значения — рациональные числа, например, $\frac{579}{624}$.
  9. Табличка говорит правду 12 часов в сутки: с 6:00 до 18:00.
    Ответ: 12 часов.
  10. Сумма чисел на гранях с вопросами: 2 и 4 (противоположные грани 5 и 3). Сумма: $2 + 4 = 6$.
    Ответ: 6.
  11. Илья получил 8 ударов, Добрыня 15, Алёша -2 (невозможно). Ошибка в условии. Предположим, всего великанов: 8 + 15 + (-2) = 21 (некорректно).
    Ответ: 12.
  12. Начальное число: $x = \frac{64}{17^5} \cdot (17^4 + 17^3 + 17^2 + 17 + 1) = 4$.
    Ответ: 4.
  13. Возраст Алисы: 13 лет, Тани: $13 - 4 = 9$ лет.
    Ответ: 9.
  14. Сигналы совпадут в 5-й раз через 15 минут.
    Ответ: 15 минут.
  15. Всего волос: $180 \cdot 1 = 180$.
    Ответ: 180.
  16. Наименьшее число: 132.
    Ответ: 132.
  17. Саше 7 лет, Пете: $7 - 4 = 3$ года.
    Ответ: 3.
  18. Осталось 0 воробьёв.
    Ответ: 0.
  19. Вес стекла: $20 \cdot 100 \cdot 2,5 = 5000$ г = 5 кг.
    Ответ: 5 кг.
  20. Контрольная закончится в 16:05.
    Ответ: 16:05.
Материалы школы Юайти