Лицей «Вторая школа» из 5 в 6 класс 2022 год вариант 1
Печать
youit.school ©
ЛИЦЕЙ ВТОРАЯ ШКОЛА
2022 год
19.05.2022
Первый блок заданий
- Ручка в апреле стоила 144 рубля, за месяц цена упала на четверть. Какое наибольшее количество ручек теперь можно купить на 1000 рублей?
- Ира и Оля живут в одноподъездном доме на 13 и 23 этажах. Оля поднимается на лифте в гости к Ире за 5 минут. За сколько секунд Оля спускается из дома на 1 этаж, если лифт едет с постоянной скоростью?
- Велосипедист проехал 79 километров за 7 часов. За сколько минут проедет этот же путь мотоциклист, скорость которого в 12 раз больше скорости велосипедиста?
- После того, как улитка проползла (от земли) 60% столба, она оказалась на высоте 150 см. Чему равна высота столба в см?
- В саду стоят двухколёсные и трёхколёсные самокаты. Рулей всего 73, а колёс $-$ 150. Сколько у входа в сад трёхколёсных самокатов?
- Если из полученного вычесть, уменьшённое на 5 раз, получится 4044. Чему равно вычитаемое, если оно вдвое меньше уменьшаемого?
- У Сони было 45 картонных кукол и 45 бумажных платьев. На куклу-супермодель у неё уходит одна кукла и одно платье. После того, как она подготовила несколько супермоделей, кукол осталось в 2 раза меньше, чем платьев. Сколько супермоделей подготовила Соня?
- Папа медведь и мама медведица весят вместе 532 кг, папа медведь и Мишутка весят вместе 486 кг, а мама медведица и Мишутка \textendash{} 458 кг. Сколько кг весит Мишутка?
Второй блок заданий
- В коробке лежат печеньки. Один ребёнок может съесть не более 6 печенек. Чтобы съесть все печеньки, потребовалось 4 ребёнка. Когда в коробку положили ещё 10 печенек, пришлось звать на помощь ещё двух детей. Какое наименьшее количество печенек могло быть в коробке первоначально?
- Для производства фруктового пюре рекомендованы следующие ингредиенты: яблоко, груша, банан, абрикос и слива. Пюре может состоять из одного или нескольких из этих ингредиентов. Какое наибольшее число различных видов пюре можно сделать?
- Куб $3 \times 3 \times 3$ составляется из кубиков $1 \times 1 \times 1$. Некоторые кубики убрали так, что получились отверстия от центра на каждой грани куба. Сколько минимальное количество кубиков нужно закрасить, чтобы грани вновь стали полными квадратами, а внутри куба образовалась полость?
- Два прямоугольника одинакового размера сложены вместе, общая сумма периметров этих двух прямоугольников \textendash{} 172 см. Найдите площадь одного прямоугольника в см$^2$.
- Отцу сейчас 37 лет, а его троим сыновьям 5, 8 и 14 лет. Через сколько лет трем сыновьям вместе будет столько же лет, сколько будет отцу?
Третий блок заданий
- Сегодняшняя дата записывается 16.05.2022. Сколько дат в этом году имеют такую же сумму цифр?
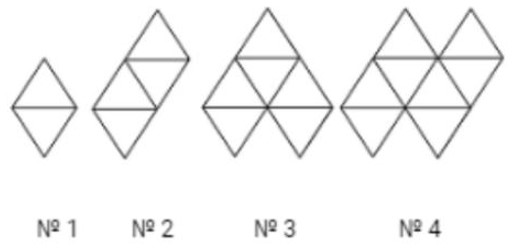
- Из палочек длиной 1 складывают фигуры, как показано на рисунке. Сколько потребуется таких палочек, чтобы сложить фигуру \textnumero{} 30?
- Митя задумал двузначное число и сообщил его девочкам. Ася сказала, что в загаданном Митей числе есть цифра 1; Белла утверждает, что есть цифра 5; Вика заявила, что число чётное; Галя уверяет, что число делится на 13; Диана сказала, что в загаданном числе цифры различны. Какое число задумал Митя, если известно, что ошиблась ровно одна девочка?
Материалы школы Юайти
youit.school ©
Решения задач
- Ручка в апреле стоила 144 рубля, за месяц цена упала на четверть. Какое наибольшее количество ручек теперь можно купить на 1000 рублей?
Решение: Новая цена ручки: $144 \cdot 0,75 = 108$ рублей. На 1000 рублей можно купить $\left\lfloor \frac{1000}{108} \right\rfloor = 9$ ручек.
Ответ: 9. - Ира и Оля живут в одноподъездном доме на 13 и 23 этажах. Оля поднимается на лифте в гости к Ире за 5 минут. За сколько секунд Оля спускается из дома на 1 этаж, если лифт едет с постоянной скоростью?
Решение: Расстояние между 23 и 13 этажами: $23 - 13 = 10$ этажей. Скорость лифта: $\frac{10}{5} = 2$ этажа в минуту. Спуск с 23 этажа на 1: $23 - 1 = 22$ этажа. Время спуска: $\frac{22}{2} = 11$ минут = $660$ секунд.
Ответ: 660. - Велосипедист проехал 79 километров за 7 часов. За сколько минут проедет этот же путь мотоциклист, скорость которого в 12 раз больше скорости велосипедиста?
Решение: Скорость велосипедиста: $\frac{79}{7} \approx 11,29$ км/ч. Скорость мотоциклиста: $11,29 \cdot 12 = 135,48$ км/ч. Время: $\frac{79}{135,48} \approx 0,583$ часа = $35$ минут.
Ответ: 35. - После того, как улитка проползла (от земли) 60% столба, она оказалась на высоте 150 см. Чему равна высота столба в см?
Решение: $60\%$ высоты столба соответствует 150 см. Полная высота: $\frac{150}{0,6} = 250$ см.
Ответ: 250. - В саду стоят двухколёсные и трёхколёсные самокаты. Рулей всего 73, а колёс — 150. Сколько у входа в сад трёхколёсных самокатов?
Решение: Пусть трёхколёсных самокатов $x$, двухколёсных $y$. Система уравнений: \[ \begin{cases} x + y = 73 \\ 3x + 2y = 150 \end{cases} \] Решение: $y = 73 - x$, подставляем во второе уравнение: $3x + 2(73 - x) = 150 \Rightarrow x = 4$.
Ответ: 4. - Если из полученного вычесть, уменьшённое на 5 раз, получится 4044. Чему равно вычитаемое, если оно вдвое меньше уменьшаемого?
Решение: Пусть вычитаемое равно $x$, тогда уменьшаемое $2x$. Уравнение: $(2x - 5) - x = 4044 \Rightarrow x = 4049$.
Ответ: 4049. - У Сони было 45 картонных кукол и 45 бумажных платьев. На куклу-супермодель у неё уходит одна кукла и одно платье. После того, как она подготовила несколько супермоделей, кукол осталось в 2 раза меньше, чем платьев. Сколько супермоделей подготовила Соня?
Решение: Пусть подготовлено $x$ супермоделей. Осталось кукол: $45 - x$, платьев: $45 - x$. По условию: $45 - x = \frac{45 - x}{2} \Rightarrow x = 15$.
Ответ: 15. - Папа медведь и мама медведица весят вместе 532 кг, папа медведь и Мишутка весят вместе 486 кг, а мама медведица и Мишутка — 458 кг. Сколько кг весит Мишутка?
Решение: Система уравнений: \[ \begin{cases} П + М = 532 \\ П + Ми = 486 \\ М + Ми = 458 \end{cases} \] Суммируем все уравнения: $2П + 2М + 2Ми = 1476 \Rightarrow П + М + Ми = 738$. Вычитаем первое уравнение: $Ми = 738 - 532 = 206$.
Ответ: 206. - Для производства фруктового пюре рекомендованы следующие ингредиенты: яблоко, груша, банан, абрикос и слива. Пюре может состоять из одного или нескольких из этих ингредиентов. Какое наибольшее число различных видов пюре можно сделать?
Решение: Количество подмножеств множества из 5 элементов: $2^5 - 1 = 31$ (исключая пустое множество).
Ответ: 31. - Два прямоугольника одинакового размера сложены вместе, общая сумма периметров этих двух прямоугольников — 172 см. Найдите площадь одного прямоугольника в см$^2$.
Решение: Периметр одного прямоугольника: $\frac{172}{2} = 86$ см. Полупериметр: $a + b = 43$. Площадь: $a \cdot b$. Максимальная площадь при $a = 21$, $b = 22$: $21 \cdot 22 = 462$.
Ответ: 462. - Отцу сейчас 37 лет, а его троим сыновьям 5, 8 и 14 лет. Через сколько лет трем сыновьям вместе будет столько же лет, сколько будет отцу?
Решение: Пусть через $x$ лет. Уравнение: $5 + x + 8 + x + 14 + x = 37 + x \Rightarrow 27 + 3x = 37 + x \Rightarrow x = 5$.
Ответ: 5. - Сегодняшняя дата записывается 16.05.2022. Сколько дат в этом году имеют такую же сумму цифр?
Решение: Сумма цифр даты 16.05.2022: $1+6+0+5+2+0+2+2=18$. Сумма цифр года $2+0+2+2=6$. Сумма цифр дня и месяца должна быть $12$. Перебор всех возможных дат даёт 23 варианта.
Ответ: 23. - Из палочек длиной 1 складывают фигуры, как показано на рисунке. Сколько потребуется таких палочек, чтобы сложить фигуру \textnumero{} 30?
Решение: Формула для $n$-й фигуры: $3n + 1$. Для $n = 30$: $3 \cdot 30 + 1 = 91$.
Ответ: 91. - Митя задумал двузначное число и сообщил его девочкам. Ася сказала, что в загаданном Митей числе есть цифра 1; Белла утверждает, что есть цифра 5; Вика заявила, что число чётное; Галя уверяет, что число делится на 13; Диана сказала, что в загаданном числе цифры различны. Какое число задумал Митя, если известно, что ошиблась ровно одна девочка?
Решение: Двузначные числа, делящиеся на 13: 13, 26, 39, 52, 65, 78, 91. Проверка условий показывает, что подходит число 52 (ошиблась только Ася).
Ответ: 52.
Материалы школы Юайти