Лицей «Вторая школа» из 5 в 6 класс 2000 год вариант 1-2

1. Футбол. В команде 22 футболиста. 9 из них умеют бить по воротам с левой ноги, 14 — с правой, из которых 6 умеют делать и то, и другое. Остальные футболисты умеют бить только головой. Сколько футболистов не умеют бить ногами?
2. Годы. Маме сейчас 35 лет, папе 39, а их детям 8, 10, 12 и 14 лет. Через сколько лет всем детям вместе будет столько же лет, сколько будет маме и папе вместе?
3. Движение. Маша и Саша, поссорившись, пошли с равными скоростями в противоположные стороны. Через 4 минуты Саша решил помириться и, развернувшись, стал догонять Машу, увеличив скорость в 3 раза. Сколько пройдет минут, когда он догонит Машу?
4. Цирк. В цирке есть только тигры, львы и обезьяны. Тигров в 3 раза меньше, чем львов и обезьян вместе, а обезьян в 2 раза больше, чем тигров и львов вместе. Сколько в цирке тигров, если львов 5?
5. Прогнозы. Сделаны четыре прогноза на победу в шахматном турнире: 1) победит Петя, 2) победит не Коля, 3) победит Аня; 4) победит не Аня. В турнире оказался один победитель и при этом ровно один прогноз оказался верным. Кто победил в турнире?
6. Доска. Мудрец изобрёл новый вид шахмат. В них играют на квадратной доске с шахматной раскраской, на которой 85 чёрных клеток. А сколько на этой доске белых клеток?
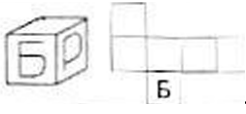
7. Кубик. На гранях кубика нарисованы буквы «Б» и «Р». Изобразите на развертке кубика положение буквы «Р» (на какой грани она находится и как повернута).
   
   
   
   
8. Леденцы. В ящике для сладкоежек есть много красных, жёлтых и зелёных леденцов. Какое наименьшее число леденцов надо взять наудачу из ящика, чтобы каждому из трёх человек можно было дать по 6 леденцов одного цвета (не важно, какого)?
9. Квадрат. Найдите наименьшее натуральное число, которое больше 8100, и которое является квадратом натурального числа.
10. Цена. За книгу заплатили 77 руб. и осталось заплатить ещё столько, сколько осталось бы заплатить, если бы за неё заплатили столько, сколько осталось заплатить. Сколько стоит эта книга?
11. Монеты. У Пети в кармане несколько монет, причём среди любых четырёх найдётся монета 1 рубль, а среди любых пяти найдётся монета 2 рубля. Петя вытащил из кармана 7 монет. Какие это монеты?
12. Ряд. Первое число 52, затем у каждого числа находят сумму цифр и умножают её на 13 — это следующее число. Например, второе число $(5+2)\times13=91$. Какое число стоит на 2022-м месте?
13. Ладья. Ладья обошла все клетки доски $90\times90$ по одному разу и вернулась в исходную клетку. Центры клеток соединили по порядку, в котором ладья их обошла. Получилась замкнутая ломаная. Найдите длину этой ломаной, если сторона клетки равна 1 см. Почему длина ломаной всегда одна и та же?
14. Квадраты. На клетчатом листе нарисован прямоугольник, состоящий из квадратов. Квадраты состоят из целого числа клеток размером 1 см. По вертикали сторона прямоугольника равна 94 см. Какова ширина прямоугольника по горизонтали в сантиметрах?
    
    
    
    
15. Прирост. От каждой стороны исходного прямоугольника отступили на 3 см во внешнюю сторону и получили новый прямоугольник. На сколько больше площадь нового прямоугольника, чем исходного, если периметр исходного равен 100 см?
    
    
    
    
16. Делители. В последовательности $1;1;2;3;5;8;13;21;\dots$ каждое очередное число равно сумме двух предыдущих. Могут ли в ней оказаться рядом два числа, делящиеся на 7? Если «да», приведите пример; если «нет», объясните почему.

Решения задач

1. В команде 22 футболиста. Через объединение множеств: футболисты, умеющие бить ногами: \(9 + 14 - 6 = 17\). Не умеют бить ногами: \(22 - 17 = 5\).
   Ответ: 5.
2. Сумма возрастов детей: \(8 + 10 + 12 + 14 = 44\). Сумма родителей: \(35 + 39 = 74\). Через \(x\) лет: \(44 + 4x = 74 + 2x \Rightarrow x = 15\).
   Ответ: 15.
3. Первоначальное расстояние: \(8v\). Относительная скорость после увеличения: \(3v - v = 2v\). Время сближения: \(\frac{8v}{2v} = 4\) минуты.
   Ответ: 4 минуты.
4. Пусть тигры \(T\), обезьяны \(O\). Уравнения: \(T = \frac{5 + O}{3}\), \(O = 2(T + 5)\). Подставляем \(T = \frac{5 + O}{3}\): \(O = 2\left(\frac{5 + O}{3} + 5\right) \Rightarrow O = 20\), тогда \(T = 5\).
   Ответ: 5.
5. Если победил Коля, верен только прогноз 4 («не Аня»). Для других победителей количество верных прогнозов больше.
   Ответ: Коля.
6. Доска размера \(13×13\), черных клеток 85. Белых клеток: \(13×13 - 85 = 84\).
   Ответ: 84.
7. На центральной грани развертки буква «Р» ориентирована горизонтально вправо (предполагаемая конфигурация кубика).
   Ответ: Буква «Р» на передней грани, направлена вправо.
8. Наихудший случай: 15 леденцов (5 каждого цвета), следующая взятая обеспечит 6 одного цвета. Требуется \(5 \times 2 + 6 + 1 = 17\).
   Ответ: 17.
9. Наименьший квадрат больше 8100: \(91^2 = 8281\).
   Ответ: 8281.
10. Пусть цена \(x\). Из условий: \(x = 77 + y\), \(y = x - y \Rightarrow x = 2y \Rightarrow y = 77\). Итог: \(x = 154\).
    Ответ: 154 руб.
11. Среди любых четырёх монет есть 1 рубль ⇒ максимум 3 монеты других. Среди пяти есть 2 рубля ⇒ максимум 4 других. Петя вытащил 7 монет: \(4 \times 1\) и \(3 \times 2\).
    Ответ: 4 монеты по 1 рублю и 3 монеты по 2 рубля.
12. Последовательность циклична с периодом 3: 52 → 91 → 130 → 52. \(2022 \mod 3 = 0 ⇒\) третий элемент цикла.
    Ответ: 130.
13. Каждая клетка посещена один раз, переходы между центрами — 8100 см. Замкнутая ломаная: переходы равны количеству клеток.
    Ответ: 8100 см, так как ладья проходит 8100 см при обходе всех клеток.
14. Сторона квадрата делит 94 см. Наибольший общий делитель 94 — 47 см. Ширина: 47 см.
    Ответ: 47 см.
15. Площадь нового прямоугольника: \((a + 6)(b + 6)\). Разность: \(6(a + b) + 36 = 6 \times 50 + 36 = 336\).
    Ответ: На 336 см².
16. Период Фибоначчи по модулю 7 не содержит двух нулей подряд. Следовательно, два числа подряд делящихся на 7 невозможны.
    Ответ: Нет.