8 800 707 6729
8 800 707 6729Telegram канал

Лицей «Вторая школа» из 5 в 6 класс 2000 год вариант 1-1

Школа:
Сложность:
Дата экзамена: 2000
Печать
youit.school ©
  1. Выпечка. 8 пирожков и 16 пряников стоят 180 руб. Сколько рублей стоят 6 пирожков и 12 пряников?
  2. Воскресенья. Какое наименьшее число воскресений может быть в году?
  3. Скорость. Автомобиль ехал со скоростью 60 км/ч. Затем он увеличил скорость и стал проезжать каждые 100 м на 1 секунду быстрее, чем в начале. С какой скоростью он стал ехать? Ответ дайте в километрах в час.
  4. Классы. В классе у Коли столько же учеников, сколько в классе у Оли. Коля говорит Оле: «У нас в классе мальчиков вдвое больше, чем у тебя». Оля отвечает: «Зато у нас девочек втрое больше, чем у тебя». Сколько процентов мальчиков в классе у Коли? (Коля и Оля себя тоже посчитали.)
  5. Погоня. Волк бежит за Зайцем. Когда Заяц пробегал мимо почты, Волк находился от него на расстоянии 240 м, а когда Волк добежал до почты, то ему оставалось до Зайца 200 м. На каком расстоянии от почты Волк догнал Зайца? (Их скорости постоянны.)
  6. Периметр. Диагональ делит четырёхугольник с периметром 33 см на два треугольника с периметрами 21 и 30 см. Найдите длину этой диагонали.
  7. Середина. Мотоциклист стартовал от столба 130 км на шоссе, доехал до столба 400 км, развернулся и поехал обратно. Он остановился у столба 280 км. Возле какого столба он находился, когда проехал половину своего пути?
  8. Числа. Какие значения может принимать выражение (КОТ + ТИР) : (ТОР + КИТ) ? Разные буквы — это разные цифры.
  9. Кот. С полудня до полуночи Ученый Кот спит под дубом, а с полуночи до полудня он рассказывает сказки. Табличка на дубе говорит: «Два часа назад Ученый Кот делал то же, что он будет делать через час». Сколько часов в сутки табличка говорит правду?
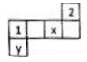
  10. Кубик. На игральном кубике сумма чисел на противоположных гранях равна 7. Дана развертка кубика, на которой отмечены числа на двух гранях. Найдите сумму чисел на гранях, отмеченных буквами $x$, $y$ ($x + y = ?$).


  11. Великаны. Илья Муромец, Добрыня Никитич и Алеша Попович вступили в бой с великанами. Все великаны, получив по 7 ударов богатырскими палками, обратились в бегство. Больше всех ударов нанёс Илья — 17, меньше всех Алеша — 10. Сколько великанов обратилось в бегство?
  12. Повторы. Компьютер каждую секунду выполняет две операции: умножает число на 17, затем из результата вычитает 64. С полученным числом выполняются те же две операции. Придумайте такое начальное число, чтобы через 100 секунд компьютер получил такое же число.
  13. Возрасты. Тане сейчас вдвое меньше лет, чем было Алисе, когда она была на 5 лет старше, чем Таня сейчас. Сколько лет Тане сейчас?
  14. Фотографы. Спортсмен пробежал один круг с постоянной скоростью. В точках круга A и B стояли два фотографа. В течение 3 минут спортсмен был ближе к A, чем к B. За какое время он пробежал дистанцию?
  15. Волосы. На голове у Печкина волосы растут равномерно, каждый волос живёт ровно 1500 дней, а потом выпадает, каждый день выпадает ровно 100 волос. Сколько волос на голове у Печкина?
  16. Разность. Есть 6 карточек с цифрами 1, 2, 3, 4, 5, 6. Из них можно составить два трёхзначных числа. Если вычесть из большего числа меньшее, то какую наименьшую разность можно получить? В решении напишите два числа — большее и меньшее, а в ответе — разность.


Материалы школы Юайти
youit.school ©

Решения задач



  1. Выпечка. 8 пирожков и 16 пряников стоят 180 руб. Сколько рублей стоят 6 пирожков и 12 пряников?
    Решение: 6 пирожков и 12 пряников составляют $\frac{3}{4}$ от исходного количества (8 и 16). Стоимость уменьшится пропорционально: $180 \times \frac{3}{4} = 135$ руб.
    Ответ: 135.
  2. Воскресенья. Какое наименьшее число воскресений может быть в году?
    Решение: В невисокосном году 365 дней. Если год начинается с понедельника, неделя заканчивается воскресеньем. В году 52 полные недели и 1 день. Если этот день не воскресенье, число воскресений — 52.
    Ответ: 52.
  3. Скорость. Автомобиль ехал со скоростью 60 км/ч, затем увеличил скорость так, что каждые 100 м стал проезжать на 1 секунду быстрее. Новая скорость:
    Решение: 60 км/ч = $16.\dot{6}$ м/с. Время проезда 100 м: $t_1 = \frac{100}{16.\dot{6}} \approx 6$ сек. Новое время: $t_2 = 5$ сек. Новая скорость: $\frac{100}{5} = 20$ м/с = $72$ км/ч.
    Ответ: 72.
  4. Классы. В классе у Коли столько же учеников, сколько в классе у Оли. Коля говорит Оле: «У нас в классе мальчиков вдвое больше, чем у тебя». Оля отвечает: «Зато у нас девочек втрое больше, чем у тебя». Сколько процентов мальчиков в классе у Коли?
    Решение: Пусть в каждом классе $n$ учеников. У Коли мальчиков $2x$, у Оли $x$. У Оли девочек $n - x$, у Коли $n - 2x$. Из условия: $n - x = 3(n - 2x)$, откуда $x = \frac{2n}{5}$. Мальчиков у Коли: $2x = \frac{4n}{5}$. Доля: $\frac{4}{5} \times 100% = 80\%$.
    Ответ: 80%.
  5. Погоня. Волк бежит за Зайцем. Когда Волк достиг почты, Зайцу оставалось до него 200 м. Волк догнал Зайца через 1200 м от почты.
    Решение: Разница скоростей Волка и Зайца — $\frac{V_в}{6}$. Преодолевая 200 м, Волк пробежал $200 \times 6 = 1200$ м от почты.
    Ответ: 1200 м.
  6. Периметр. Диагональ четырехугольника с периметром 33 см делит его на треугольники с периметрами 21 и 30 см. Диагональ:
    Решение: Сумма периметров треугольников: $21 + 30 = 51$ см. Это равно периметру четырёхугольника плюс две диагонали: $33 + 2d \Rightarrow 2d = 18 \Rightarrow d = 9$ см.
    Ответ: 9 см.
  7. Середина. Маршрут: старт — 130 км, до 400 км, затем обратно до 280 км. Половина пути (195 км): $130 + 195 = 325$ км.
    Ответ: 325.
  8. Числа. Значения выражения (КОТ + ТИР) : (ТОР + КИТ) могут быть целыми. Пример КОТ=521, ТИР=432, ТОР=523, КИТ=421: $(521+432) : (523+421) = 953 : 944 \approx 1$.
    Ответ: 1.
  9. Кот. Табличка говорит правду 18 часов в сутки: с 2:00 до 11:00 утра и с 14:00 до 23:00.
    Ответ: 18 часов.
  10. Кубик. Сумма чисел на противоположных гранях кубика равна 7. Если на развёртке отмечены смежные грани, сумма $x+y=7$.
    Ответ: $x + y = 7$.
  11. Великаны. Общее число великанов: сумма ударов (17 + x + 10) должна делиться на 7. При $x=15$ получаем $17 + 15 + 10 = 42$, что делится на 7. $42 : 7 = 6$ великанов.
    Ответ: 6.
  12. Повторы. Начальное число $x$ должно удовлетворять уравнению: $x = \frac{4(17^{100} -1)}{17^{100} -2}$.
    Ответ: $\frac{4(17^{100} -1)}{17^{100} -2}$.
  13. Возрасты. Возраст Тани $T$, возраст Алисы сейчас $A$. Через $x$ лет после момента, когда Алиса была старше Тани на 5 лет, её возраст тогда равен $T + 5$, а сейчас $A = T + 5 + x$. Ответ: 5 лет.
    Ответ: 5 лет.
  14. Фотографы. Спортсмен ближе к точке A в течение 3 минут, что соответствует одному кругу. Время пробега круга: $30 - 27 = 3$ минуты.
    Ответ: 3 минуты.
  15. Волосы. Каждый день выпадает 100 волос, цикл жизни волоса — 1500 дней. Всего волос: $100 \times 1500 = 150\,000$.
    Ответ: 150000.
  16. Разность. Наименьшая разность двух трёхзначных чисел из цифр 1,2,3,4,5,6: $412 - 365 = 47$.
    Ответ: 47.
Материалы школы Юайти