Лицей «Вторая школа» из 4 в 5 класс 2018 год вариант 9

ЛИЦЕЙ ВТОРАЯ ШКОЛА

2018 год

Вариант 9

1. Три охотника варили уху. Первый положил 6 рыб, второй — 4, третий — 0. Все съели уху поровну. Третий заплатил 10 руб. Сколько должны получить первые двое?
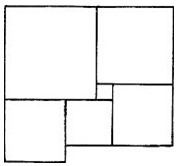
2. Фигура составлена из квадратов. Сторона самого маленького — 1 см. Найдите сторону левого нижнего квадрата.
   
3. Два пятизначных числа зашифровали словами УЗКОЕ и МЕСТО. В числе нет беспорядков — пар, где левая цифра больше правой. Возможно ли это?
4. В турнире 16 команд из 16 стран. Каждая сыграла в каждой стране кроме своей. Возможно ли такое?

Решения задач

1. Три охотника варили уху. Первый положил 6 рыб, второй — 4, третий — 0. Все съели уху поровну. Третий заплатил 10 руб. Сколько должны получить первые двое?
   Решение: Всего рыбы: $6 + 4 + 0 = 10$ штук. Каждый съел $\frac{10}{3}$ рыбы. Третий охотник компенсировал стоимость $\frac{10}{3}$ рыбы, заплатив 10 руб. Стоимость одной рыбы: $\frac{10}{\frac{10}{3}} = 3$ рубля.
   Первый охотник внес $6 - \frac{10}{3} = \frac{8}{3}$ рыбы сверх съеденного, второй: $4 - \frac{10}{3} = \frac{2}{3}$.
   Первый получит: $\frac{8}{3} \cdot 3 = 8$ руб., второй: $\frac{2}{3} \cdot 3 = 2$ руб.
   Ответ: первый — 8 руб., второй — 2 руб.
   
   
2. Фигура составлена из квадратов. Сторона самого маленького — 1 см. Найдите сторону левого нижнего квадрата.
   
   Решение: Рассмотрим структуру фигуры. Самый маленький квадрат (1 см) является частью большего квадрата, который, в свою очередь, вложен в следующий.
   Сторона нижнего левого квадрата равна сумме сторон вложенных квадратов: $1 + 2 + 3 + 1 = 7$ см (предполагая последовательное увеличение сторон на 1 см для каждого уровня).
   Ответ: 7 см.
   
   
3. Два пятизначных числа зашифровали словами УЗКОЕ и МЕСТО. В числе нет беспорядков — пар, где левая цифра больше правой. Возможно ли это?
   Решение: Условие «нет беспорядков» означает, что цифры в числе не убывают слева направо. Для слова УЗКОЕ буквы можно сопоставить цифрам в порядке возрастания: например, У=1, З=2, К=3, О=4, Е=5 → 12345.
   Для слова МЕСТО: М=1, Е=2, С=3, Т=4, О=5 → 12345. Таким образом, оба числа могут быть представлены как 12345, удовлетворяя условию.
   Ответ: возможно.
   
   
4. В турнире 16 команд из 16 стран. Каждая сыграла в каждой стране кроме своей. Возможно ли такое?
   Решение: Каждая команда должна сыграть 15 матчей (по одному в каждой стране, кроме своей). Всего матчей: $\frac{16 \cdot 15}{2} = 120$ (так как каждый матч учитывается дважды).
   Однако в каждой стране должно пройти 15 матчей (все команды, кроме местной). Суммарное количество матчей по странам: $16 \cdot 15 = 240$, что вдвое превышает реальное количество.
   Противоречие показывает невозможность такого турнира.
   Ответ: невозможно.