Лицей «Вторая школа» из 4 в 5 класс 2018 год вариант 8

ЛИЦЕЙ ВТОРАЯ ШКОЛА

2018 год

Вариант 8

1. Есть две кучи по 25 и 27 камней. Игроки по очереди делят кучу на две меньшие. Кто не может сделать ход — проиграл. Кто выигрывает?
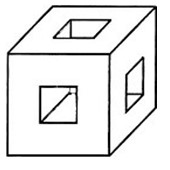
2. В центре каждой грани куба со стороной 3 см — сквозные отверстия 1×1 см. Найдите площадь поверхности оставшейся фигуры.
   
3. Петя задумал однозначное число. Вася называет любое число и спрашивает НОД с задуманным. Может ли Вася по ответу точно узнать число?
4. У четырёх человек нет троих с одинаковым именем, отчеством или фамилией. Но у каждой пары совпадает одно из трёх. Может ли такое быть?

Решения задач

1. Есть две кучи по 25 и 27 камней. Игроки по очереди делят кучу на две меньшие. Кто не может сделать ход — проиграл. Кто выигрывает?
   Решение: Проанализируем позицию с помощью понятия "ним-суммы". Для каждой кучи определим минимальное количество ходов до завершения:
   - Куча из 25 камней требует 24 делений (пока не останутся единицы)
   - Куча из 27 камней требует 26 делений
   Суммарное количество ходов: 24 + 26 = 50 (чётное число). Это означает, что второй игрок сможет зеркально повторять ходы первого, оставляя ему последний ход.
   Ответ: Второй игрок выигрывает при правильной игре.
2. В центре каждой грани куба со стороной 3 см — сквозные отверстия 1×1 см. Найдите площадь поверхности оставшейся фигуры.
   Решение:
   Исходная площадь куба: $6 \cdot 3^2 = 54$ см².
   Каждое отверстие уменьшает внешнюю площадь на $1$ см² и добавляет внутренние стенки:
   - Удалено: $6 \cdot 1 = 6$ см²
   - Добавлено внутренних стенок: $6 \cdot 4 = 24$ см² (4 стенки на каждое отверстие)
   Итоговая площадь: $54 - 6 + 24 = 72$ см².
   Ответ: 72 см².
3. Петя задумал однозначное число. Вася называет любое число и спрашивает НОД с задуманным. Может ли Вася по ответу точно узнать число?
   Решение: Нет. Для любого числа, которое назовёт Вася, НОД с разными однозначными числами может совпадать. Например:
   - Если Вася назовёт 6, НОД(6,2)=2 и НОД(6,4)=2
   - Для числа 8: НОД(8,2)=2 и НОД(8,4)=4
   Нет такого числа, которое давало бы уникальные НОДы со всеми однозначными числами.
   Ответ: Нет, не может.
4. У четырёх человек нет троих с одинаковым именем, отчеством или фамилией. Но у каждой пары совпадает одно из трёх. Может ли такое быть?
   Решение: Да. Пример:
   1. Иван Алексеевич Петров
   2. Иван Борисович Сидоров
   3. Пётр Алексеевич Сидоров
   4. Пётр Борисович Петров
   Проверка пар:
   - 1-2: имя (Иван)
   - 1-3: отчество (Алексеевич)
   - 1-4: фамилия (Петров)
   - 2-3: фамилия (Сидоров)
   - 2-4: отчество (Борисович)
   - 3-4: имя (Пётр)
   Ни в одном параметре нет трёх совпадений.
   Ответ: Да, может.