Лицей «Вторая школа» из 4 в 5 класс 2018 год вариант 4

ЛИЦЕЙ ВТОРАЯ ШКОЛА

2018 год

Вариант 4

1. Какое наименьшее число точек нужно отметить на плоскости так, чтобы после стирания любой из них среди оставшихся точек нашлись три точки, служащие вершинами равностороннего треугольника?
2. За контрольную работу каждый из 25 школьников получил «3», «4» или «5». Насколько больше было пятёрок, чем троек, если сумма оценок равна 106?
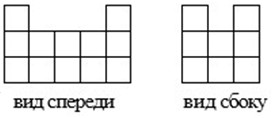
3. На площадку 3×5 клеток надо поставить кубики, чтобы башня имела виды спереди и сбоку, как на рисунке. а) Укажите в каждой клетке высоту столбика; б) Докажите, что меньшим числом кубиков обойтись нельзя.
   
4. Игра: двое по очереди записывают по одной цифре слева направо, пока не получится 12-значное число. Если оно делится на 7 — выигрывает второй. Кто может гарантировать себе победу?

Решения задач

1. Какое наименьшее число точек нужно отметить на плоскости так, чтобы после стирания любой из них среди оставшихся точек нашлись три точки, служащие вершинами равностороннего треугольника?
   Решение: Рассмотрим конфигурацию из семи точек: правильный шестиугольник с центром. Каждая вершина и центр образуют равносторонние треугольники с соседними вершинами. При удалении любой вершины останется пять точек, среди которых найдутся три вершины равностороннего треугольника. Если удалить центр, останутся шесть вершин шестиугольника, из которых также можно выбрать равносторонний треугольник. Меньше семи точек недостаточно, так как при удалении одной из шести точек может не остаться тройки для треугольника.
   Ответ: 7.
2. За контрольную работу каждый из 25 школьников получил «3», «4» или «5». Насколько больше было пятёрок, чем троек, если сумма оценок равна 106?
   Решение: Пусть $x$ — количество троек, $y$ — четвёрок, $z$ — пятёрок. Составим систему: \[ \begin{cases} x + y + z = 25 \\ 3x + 4y + 5z = 106 \end{cases} \] Вычтем из второго уравнения первое, умноженное на 3: \[ y + 2z = 31 \quad \Rightarrow \quad y = 31 - 2z \] Подставим в первое уравнение: \[ x + (31 - 2z) + z = 25 \quad \Rightarrow \quad x = z - 6 \] Разность пятёрок и троек: \[ z - x = z - (z - 6) = 6 \] Ответ: 6.
3. На площадку 3×5 клеток надо поставить кубики, чтобы башня имела виды спереди и сбоку, как на рисунке.
   1. Укажите в каждой клетке высоту столбика;
   2. Докажите, что меньшим числом кубиков обойтись нельзя.
   
   Решение:
   1. Пусть вид спереди задаёт максимальные высоты столбцов: [3, 2, 4, 1, 5], а вид сбоку — максимальные высоты строк: [2, 3, 4]. В каждой клетке $(i,j)$ высота равна минимуму из соответствующих значений для столбца и строки: \[ \begin{pmatrix} 2 & 2 & 2 & 1 & 2 \\ 3 & 2 & 3 & 1 & 3 \\ 3 & 2 & 4 & 1 & 4 \\ \end{pmatrix} \]
   2. Сумма высот: $2+2+2+1+2 + 3+2+3+1+3 + 3+2+4+1+4 = 35$. Любое уменьшение высоты хотя бы в одной клетке нарушит условие видимости.
   Ответ: а) Указанная матрица; б) 35 кубиков — минимальное количество.
4. Игра: двое по очереди записывают по одной цифре слева направо, пока не получится 12-значное число. Если оно делится на 7 — выигрывает второй. Кто может гарантировать себе победу?
   Решение: Второй игрок может контролировать остаток от деления на 7. На каждом шаге он выбирает цифру так, чтобы текущее число $N_k$ (из $k$ цифр) удовлетворяло $N_k \equiv r_k \pmod{7}$, где $r_k$ заранее определён. Поскольку на последнем шаге $N_{12} \equiv 0 \pmod{7}$, второй игрок всегда может подобрать цифру для достижения нужного остатка.
   Ответ: Второй игрок.