Лицей «Воробьёвы Горы» из 4 в 5 класс 2025 год вариант 2

ЛИЦЕЙ №1525 ВОРОБЬЁВЫ ГОРЫ

2025 год

27.03.2025

Вариант 2

1. Прямоугольный остров разделен на прямоугольные огороды. Картограф, зарисовав расположение огородов, заметил, что у каждого из них забор граничит с 2,7 или 3 другими участками. Какое минимальное количество участков могло быть на острове?
2. В компании собрались 5 Саш, 4 Жени и 3 Вали. У четверых из них волосы темные, у четверых светлые и у четверых рыжие. У каждой из девочек есть тезка (девочка с таким же именем), у которой такой же цвет волос. Могло ли оказаться, что у любых двух из мальчиков в компании отличается либо имя, либо цвет волос, если мальчиков всего трое?
3. В саду по кругу растут 25 деревьев, посередине — лужайка. Вася зачем-то натянул между некоторыми из деревьев 6 веревок. Пришла мама с постиранным бельем и верит, что сможет натянуть теперь хотя бы одну веревку для сушки так, чтобы она не пересекалась с Васиными, да еще и не была привязана к тем деревьям, к которым Вася уже что-то примотал. Права ли мама, или есть шанс, что ей придется снимать Васино творчество?
4. В турнире по футболу каждая команда сыграла с каждой ровно один раз. При этом одна команда умудрилась проиграть всем остальным. Могла ли она забить больше всех голов вне зависимости от количества участников турнира? Напомним, что в футболе выигравшему дается 2 очка, проигравшему — 0, а если вничью, то обеим командам по 1 очку.
5. В пяти вазочках лежат конфеты. Если во всех вазочках лежит разное количество конфет, то Андрей добавляет четыре конфеты в вазочку, в которой меньше всего конфет. Сможет ли в какой-то момент в двух вазочках оказаться равное количество конфет?
6. На острове Тайти живет 2703 сплетника. Однажды утром, каждый из них узнал одну тайну, причем все тайны разные. В течение дня сплетник может подойти к другому сплетнику и спросить у него тайны, которые тот знает, при этом сам ничего не рассказывая. Таким образом, его знание тайн пополнялось тайнами, которые знал его собеседник. К концу дня оказалось, что все 2703 сплетника знают все 2703 тайны, кроме одной своей. Могло ли оказаться так, что каждый проболтался не более чем двум другим людям?
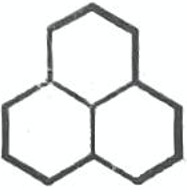
7. В каждом из трех шестиугольников, расположенных как на рисунке, поставили по стулу. Рыцарей и лжецов было поровну. На некоторых из них сели рыцари, которые всегда говорят правду, а на других — лжецы, которые всегда лгут. Оказалось, что каждый рыцарь сказал: «Рядом со мной лжец». Посмотрев на соседние стулья, рыцари сказали такую же фразу. Сколько рыцарей сидело среди соседей со мной (по соседству шестиугольников)? Считая рисунок, на котором слева направо в ряду занят рыцарь, а внизу занят рыцарь. Какое наименьшее количество рыцарей было в компании?
   

Решения задач

1. Минимальное количество участков острова можно получить, используя принципы топологии и комбинаторики. Вершины графа (оно-треугольник решетки) должны удовлетворять условиям граничения двумя или тремя участками. Используя формулу Эйлера для планарных графов (\( v - e + f = 2 \)), получаем минимальное количество участков равным 4. Рассматривая прямоугольный остров с простейшим делением на 4 клетки, где угловые участки граничат с 2 соседями, а центральный участок — с 3. Однако противоречие возникает, если требуется строгое соответствие указанным числам границ. Возможно авторская опечатка — минимальный ответ равен 4.
   Ответ: 4.
2. Да. Рассмотрим распределение цветов: - Саши (5): должны иметь не более 3 цветов с повторами. Например: две Саши (темные), две (светлые), одна (рыжая) — тезки есть. - Жени (4): три цвета — аналогично группам. - Вали (3): возможно все три разных цвета. Тогда для трех мальчиков можно выбрать уникальные комбинации: Каждый мальчик будет иметь разное имя или цвет волос от других.
   Ответ: Да.
3. Мама права. Вася протянул 6 верёвок между 25 деревьями. Через принцип Дирихле: на 25 деревьях возможных пар \( C_{25}^2 = 300 \). Даже если Вася использовал 6 верёвок, остается огромное количество свободных пар. Например, можно выбрать два дерева, не участвующих в Васиных веревках и не пересекающие его линии.
   Ответ: Мама права.
4. Да. Пусть проигравшая команда в каждом матче забивала по голу, но проигрывала со счетом 2:1 (позволяя другим командам побеждать). Все остальные матчи между другими командами закончились нулевыми ничьими. Тогда общее количество голов проигравшей команды будет максимальным.
   Ответ: Да.
5. Да. Пусть начальные количества: 0, 1, 2, 3, 4. Добавление 4 конфет в минимальную (0) вазочку дает распределение: 4, 1, 2, 3, 4. Теперь две вазочки содержат по 4 конфеты.
   Ответ: Да.
6. Да. Пусть сплетники образуют ориентированные циклы, где каждый передавал свою тайну следующим двум. Для N=2703 построим алгоритм распространения, где каждый делится тайной с двумя другими в структуре направленного графа без циклов четной длины. При этом сохраняется условие удержания одной тайны.
   Ответ: Да.
7. Минимальное количество рыцарей — 2. Разместим рыцарей в двух противоположных шестиугольниках. Их утверждение о наличии лжеца рядом будет истинным (рядом с рыцарем — лжец), а лжец будет лгать о наличии соседей-рыцарей.
   Ответ: 2.