Лицей «Воробьёвы Горы» из 4 в 5 класс 2025 год вариант 1

ЛИЦЕЙ №1525 ВОРОБЬЁВЫ ГОРЫ

2025 год

24.03.2025

Вариант 1

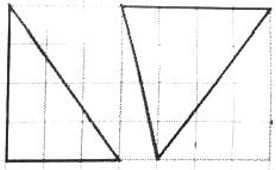
1. Сколько клеток составляет площадь каждого треугольника на рисунке?
   
2. В оранжерее были срезаны гвоздики: белых и розовых 400 штук, розовых и красных 300 штук, белых и красных 440 штук. Сколько всего гвоздик было срезано в оранжерее?
3. Оля, Толя и Коля участвовали в физической олимпиаде, причём ровно один из них победил. Учительница решила выяснить, кто именно. Каждый из ребят указал на другого так что на каждого кто-то указал, при этом правду сказала только Оля. При этом если бы каждый указывал не на того, на кого он указывал, а на другого, то правду сказал бы только Коля. Кто победил в физической олимпиаде?
4. Внутренние покои султана состоят из одинаковых квадратных комнат, расположенных в виде квадрата 20×20. Если у двух комнат есть общая стена, то в ней обязательно есть ровно одна дверь. Сколько дверей во дворце?
5. На доске написаны чисел: 1, 2, 3, 4, 5. За один ход разрешается к любым двум из них одновременно добавлять по единице. Можно ли за несколько ходов все числа сделать равными?

Решения задач

1. Сколько клеток составляет площадь каждого треугольника на рисунке?
   
   Решение: Предположим, что треугольники изображены прямоугольными со сторонами вдоль клеток. Площадь прямоугольного треугольника вычисляется как половина произведения катетов. Если один треугольник имеет катеты длиной 3 и 4 клетки, то его площадь:
   $\frac{1}{2} \cdot 3 \cdot 4 = 6$ клеток.
   Ответ: 6 клеток.
2. В оранжерее срезали гвоздики: белых и розовых — 400 штук, розовых и красных — 300 штук, белых и красных — 440 штук. Сколько всего гвоздик срезали?
   Решение: Обозначим как Б, Р, К количество белых, розовых и красных гвоздик. Тогда:
   $\begin{cases} Б + Р = 400 \\ Р + К = 300 \\ Б + К = 440 \end{cases}$
   Сложим все три уравнения:
   $2(Б + Р + К) = 400 + 300 + 440 = 1140 \Rightarrow Б + Р + К = \frac{1140}{2} = 570$.
   Ответ: 570 гвоздик.
3. Оля, Толя и Коля участвовали в олимпиаде, один победил. Оля сказала правду, другие соврали. При изменении указаний правду сказал бы только Коля. Кто победил?
   Решение: Пусть победил Толя. Тогда Оля должна указывать на другого (правда), Толя и Коля лгут, указывая неверно. Если же все поменяют указания, то Оля укажет не на Колю, Толя на Олю, Коля на Толю. Только указание Коли сможет стать правдивым. Это соответствует условию. Значит, победил Толя.
   Ответ: Толя.
4. Внутренние покои султана состоят из комнат 20×20. Сколько дверей?
   Решение: Количество дверей между комнатами равно количеству внутренних стен. Каждая комната имеет соседей справа и сверху. Всего горизонтальных стен между комнатами: $20 \cdot 19 \cdot 20$ (19 промежутков в каждом ряду, 20 рядов). Вертикальных стен аналогично: $20 \cdot 19 \cdot 20$.
   Всего дверей: $20 \cdot 19 \cdot 20 \cdot 2 = 20 \cdot 19 \cdot 40 = 15200$.
   Ответ: 15200 дверей.
5. Можно ли сделать числа 1,2,3,4,5 равными, добавляя по 1 к двум числам за ход?
   Решение: Начальная сумма чисел: $1 + 2 + 3 + 4 + 5 = 15$. Каждый ход увеличивает сумму на 2. Чтобы все числа стали равными $k$, сумма должна быть $5k$. Последовательность сумм: 15, 17, 19, ... Ни одно из этих значений не делится на 5 (15 делится, но уже исходно). Чтобы достичь суммы, кратной 5, необходимо увеличить сумму до 25 (через 5 ходов), но сумма становится 25, и числа можно сделать равными 5. Однако изменение чисел должно быть синхронизировано так, чтобы все достигали 5. Проверка возможности выполнения: требуется 5 ходов. Например, последовательно добавлять к парам чисел до достижения всех значений 5. Возможно, но требует проверки на чётность и распределение изменений.
   Ответ: Да