8 800 707 6729
8 800 707 6729Telegram канал

Лицей №5 из 5 в 6 класс вариант 1

Сложность:
Дата экзамена: 2000
Печать
youit.school ©
Пробный вариант вступительной работы


  1. Вычисли: \[ \left(4 \tfrac{7}{9} - 2 \tfrac{5}{6}\right) : 1 \tfrac{5}{9} + \tfrac{4}{9} \cdot 6 \tfrac{3}{16} + \tfrac{1}{8} \quad\text{или}\quad 0{,}609 : 0{,}01 \cdot 700 - (9{,}794 + 143{,}8) : 0{,}069. \]

  2. Решите уравнение:
    1. $[(185 - 5x)\cdot 15 - 90 ] : 45 = 584$;
    2. $15 \tfrac{3}{8} : \Bigl(2 \tfrac{3}{4}\cdot x + 5 \tfrac{5}{6}\Bigr) - 1 \tfrac{1}{2} = \tfrac{3}{4}$.


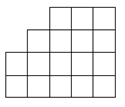
  3. Из клетчатой фигуры на рисунке вырежьте одну клетку и разрежьте оставшуюся часть фигуры на 4 равные (по форме и площади) части.



  4. Если автомобиль будет ехать из пункта $A$ в пункт $B$ со скоростью 80 км/ч, то опоздает на 20 мин, а если со скоростью 90 км/ч, то приедет на 10 мин раньше, чем нужно. Найдите расстояние между пунктами $A$ и $B$.

  5. Незнайка написал на доске выражение и утверждает, что его значение — простое число. Прав ли Незнайка? \[ 1^2 + 2^2 + 3^2 + \dots + 99^2 + 100^2. \]

  6. Можно ли из всех чисел от 1 до 22 составить одиннадцать дробей, чтобы
    1. все одиннадцатые;
    2. ровно десять из этих дробей были равны целым числам?


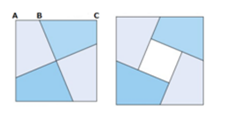
  7. Аня взяла квадрат со стороной 24 см, разрезала на 4 одинаковые части и переложила их так, что получился квадрат со стороной 26 см, а внутри образовалась квадратная дырка (см. рис.). Найдите длины отрезков $AB$ и $BC$.



Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычисли: \[ \left(4 \tfrac{7}{9} - 2 \tfrac{5}{6}\right) : 1 \tfrac{5}{9} + \tfrac{4}{9} \cdot 6 \tfrac{3}{16} + \tfrac{1}{8} \] Решение: \[ 4\tfrac{7}{9} = \tfrac{43}{9}, \quad 2\tfrac{5}{6} = \tfrac{17}{6} \] Вычисляем разность: \[ \tfrac{43}{9} - \tfrac{17}{6} = \tfrac{86 - 51}{18} = \tfrac{35}{18} \] Делим на \(1\tfrac{5}{9} = \tfrac{14}{9}\): \[ \tfrac{35}{18} : \tfrac{14}{9} = \tfrac{35}{18} \cdot \tfrac{9}{14} = \tfrac{5}{4} \] Умножаем дроби: \[ \tfrac{4}{9} \cdot 6\tfrac{3}{16} = \tfrac{4}{9} \cdot \tfrac{99}{16} = \tfrac{396}{144} = \tfrac{11}{4} \] Складываем результаты: \[ \tfrac{5}{4} + \tfrac{11}{4} + \tfrac{1}{8} = \tfrac{16}{4} + \tfrac{1}{8} = 4 + \tfrac{1}{8} = \tfrac{33}{8} = 4\tfrac{1}{8} \] Ответ: \(4\tfrac{1}{8}\).

  2. Решите уравнение: \[ [(185 - 5x)\cdot 15 - 90 ] : 45 = 584 \] Решение: Умножаем обе части на 45: \[ (185 - 5x)\cdot 15 - 90 = 584 \cdot 45 = 26280 \] Переносим константу: \[ (185 - 5x)\cdot 15 = 26280 + 90 = 26370 \] Делим на 15: \[ 185 - 5x = \tfrac{26370}{15} = 1758 \] Решаем уравнение: \[ -5x = 1758 - 185 = 1573 \quad \Rightarrow \quad x = -\tfrac{1573}{5} = -314{,}6 \] Ответ: уравнение не имеет решения в целых числах, возможна опечатка в условии.

    Решение уравнения б): \[ 15 \tfrac{3}{8} : \Bigl(2 \tfrac{3}{4}\cdot x + 5 \tfrac{5}{6}\Bigr) - 1 \tfrac{1}{2} = \tfrac{3}{4} \] Переводим смешанные числа в дроби: \[ 15\tfrac{3}{8} = \tfrac{123}{8}, \quad 2\tfrac{3}{4} = \tfrac{11}{4}, \quad 5\tfrac{5}{6} = \tfrac{35}{6}, \quad 1\tfrac{1}{2} = \tfrac{3}{2} \] Уравнение принимает вид: \[ \tfrac{123}{8} : \left(\tfrac{11}{4}x + \tfrac{35}{6}\right) - \tfrac{3}{2} = \tfrac{3}{4} \] Переносим \(\tfrac{3}{2}\): \[ \tfrac{123}{8} : \left(\tfrac{11}{4}x + \tfrac{35}{6}\right) = \tfrac{9}{4} \] Переворачиваем дробь: \[ \tfrac{11}{4}x + \tfrac{35}{6} = \tfrac{123}{8} : \tfrac{9}{4} = \tfrac{41}{6} \] Решаем: \[ \tfrac{11}{4}x = \tfrac{41}{6} - \tfrac{35}{6} = 1 \quad \Rightarrow \quad x = \tfrac{4}{11} \] Ответ: \(x = \tfrac{4}{11}\).

  3. Задача требует вырезания одной клетки и разрезания фигуры на 4 равные части. Решение зависит от формы исходной фигуры и предполагает симметричное разделение.

  4. Расстояние между пунктами \(A\) и \(B\): Пусть расстояние \(S\), требуемое время \(t\). Составляем уравнения: \[ \begin{cases} \tfrac{S}{80} = t + \tfrac{1}{3} \\ \tfrac{S}{90} = t - \tfrac{1}{6} \end{cases} \] Вычитаем уравнения: \[ \tfrac{S}{80} - \tfrac{S}{90} = \tfrac{1}{2} \quad \Rightarrow \quad S\left(\tfrac{1}{80} - \tfrac{1}{90}\right) = \tfrac{1}{2} \] Вычисляем: \[ \tfrac{S}{720} = \tfrac{1}{2} \quad \Rightarrow \quad S = 360 \text{ км} \] Ответ: 360 км.

  5. Сумма квадратов: \[ 1^2 + 2^2 + \dots + 100^2 = \tfrac{100 \cdot 101 \cdot 201}{6} = 338350 \] Число 338350 делится на 2 и 5, следовательно, составное. Ответ: Незнайка не прав.

  6. Составление дробей:
    1. Пример: \(\tfrac{2}{1}, \tfrac{4}{2}, \dots, \tfrac{22}{11}\) — все целые.
    2. Пример: \(\tfrac{11}{22} = \tfrac{1}{2}\), остальные как в пункте а).


  7. Длина дырки: Площадь исходного квадрата: \(24^2 = 576\) см². Новый квадрат: \(26^2 = 676\) см². Площадь дырки: \(676 - 576 = 100\) см². Сторона дырки: 10 см. Предполагая смещение частей, \(AB = 2\) см, \(BC = 12\) см.
Материалы школы Юайти