Лицей №239 из 9 в 10 класс 2005 год вариант 2
Печать
youit.school ©
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ № 239
2005 год
Вариант 2
- Упростить:
\[
\frac{\left(\sqrt{x} - \sqrt{y}\right)^3 + \frac{2x^2}{\sqrt{x}} + y\sqrt{y}}{x\sqrt{x} + y\sqrt{y}} + \frac{3\sqrt{xy} - 3y}{x - y}.
\]
- Решить уравнение:
\[
\frac{x^3 + 3x + 9}{x^3 + 27} - \frac{1}{x + 3} = \frac{2}{x^2 - 3x + 9}.
\]
- Решить неравенство:
\[
\frac{2x^2 + 3x - 13}{x^2 + x - 6} > 2.
\]
- Решить уравнение:
\[
(x^2 - 5x + 2)(x^2 - 5x - 1) = 28.
\]
- Решить уравнение:
\[
x + 2 - 13\sqrt{x + 2} = -42.
\]
- Решить неравенство:
\[
\left|x^2 - 4x - 14\right| < x + 10.
\]
- Построить график:
\[
y = \frac{x^2 - 6x + 5}{x - |x - 2|}.
\]
- В окружность, диаметр которой равен $\sqrt{12}$, вписан равносторонний треугольник. На его высоте, как на основании, построен правильный треугольник, в который вписана окружность. Найти радиус этой окружности.
- В трапеции $ABCD$ ($AD \parallel BC$) $AD = 2BC$. На стороне $CD$ взята точка $M$ так, что $DM = 2CM$. В каком отношении отрезок $AM$ и диагональ $BD$ делят друг друга?
- Сравнить площади прямоугольников $MNPQ$ и $ABCQ$ (см. рис).
- Существует ли треугольник, все стороны которого больше $1м$, а площадь меньше $1см^2$? Не забудьте обосновать ответ.
- Даны два утверждения:
А) Если все стороны описанного многоугольника равны, то и все его углы равны.
Б) Если все углы описанного многоугольника равны, то и все его стороны равны.
Какое из этих утверждений верно, а какое нет? (Подсказка: рассмотрите четырехугольники и пятиугольники).
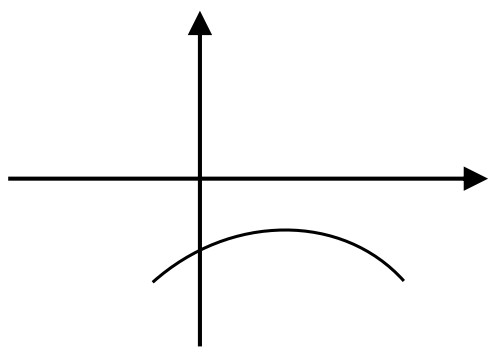
- Дано изображение графика функции $y = ax^2 + bx + c$ (см. рис.). Определить знаки коэффициентов $a$, $b$, $c$. Не забудьте обосновать ответ.
- Логарифмом числа $a > 0$ по основанию $3$ называется показатель степени, в которую нужно возвести $3$, чтобы получить $a$. Обозначение: $\log_3 a$.
Вычислить:
а) $\log_3 27$ ; $\quad$ б) $3^{\log_3 2}$ ; $\quad$ в) $9^{\log_3 7}$ ; $\quad$ г) Подумайте о том, что означает символ $\log_5 a$ и вычислите $3^{\log_5 3 \cdot \log_3 5}$
Материалы школы Юайти
youit.school ©
Решения задач
- Упростить: \[ \frac{\left(\sqrt{x} - \sqrt{y}\right)^3 + \frac{2x^2}{\sqrt{x}} + y\sqrt{y}}{x\sqrt{x} + y\sqrt{y}} + \frac{3\sqrt{xy} - 3y}{x - y}. \] Решение: Раскроем куб разности: \[ (\sqrt{x} - \sqrt{y})^3 = x\sqrt{x} - 3x\sqrt{y} + 3y\sqrt{x} - y\sqrt{y} \] Числитель первой дроби: \[ x\sqrt{x} - 3x\sqrt{y} + 3y\sqrt{x} - y\sqrt{y} + 2x\sqrt{x} + y\sqrt{y} = 3x\sqrt{x} + 3y\sqrt{x} - 3x\sqrt{y} \] Вынесем общие множители: \[ 3\sqrt{x}(x + y) - 3x\sqrt{y} = 3\sqrt{x}(x + y - \sqrt{x}\sqrt{y}) \] Знаменатель первой дроби: \[ (\sqrt{x} + \sqrt{y})(x - \sqrt{xy} + y) \] После сокращения первой дроби остается: \[ \frac{3\sqrt{x}}{x - \sqrt{xy} + y} \] Преобразуем вторую дробь: \[ \frac{3\sqrt{y}(\sqrt{x} - \sqrt{y})}{(\sqrt{x} - \sqrt{y})(\sqrt{x} + \sqrt{y})} = \frac{3\sqrt{y}}{\sqrt{x} + \sqrt{y}} \] Сумма упрощенных дробей: \[ \frac{3\sqrt{x} + 3\sqrt{y}}{x - \sqrt{xy} + y} = \frac{3(\sqrt{x} + \sqrt{y})}{(\sqrt{x} + \sqrt{y})^2} = \frac{3}{\sqrt{x} + \sqrt{y}} \] Ответ: \(\frac{3}{\sqrt{x} + \sqrt{y}}\)
- Решить уравнение: \[ \frac{x^3 + 3x + 9}{x^3 + 27} - \frac{1}{x + 3} = \frac{2}{x^2 - 3x + 9}. \] Решение: Разложим знаменатели: \[ x^3 + 27 = (x + 3)(x^2 - 3x + 9) \] Общий знаменатель уравнения: \[ (x + 3)(x^2 - 3x + 9) \] Умножим все члены уравнения на общий знаменатель: \[ (x^3 + 3x + 9) - (x^2 - 3x + 9) = 2(x + 3) \] Упростим: \[ x^3 + 3x + 9 - x^2 + 3x - 9 = 2x + 6 \] \[ x^3 - x^2 + 6x = 2x + 6 ⇒ x^3 - x^2 + 4x - 6 = 0 \] Подбором находим корень \(x = 2\). Делим многочлен на \((x - 2)\): \[ x^3 - x^2 + 4x - 6 = (x - 2)(x^2 + x + 3) = 0 \] Квадратное уравнение \(x^2 + x + 3 = 0\) не имеет действительных корней. Ответ: \(2\)
- Решить неравенство: \[ \frac{2x^2 + 3x - 13}{x^2 + x - 6} > 2. \] Решение: Перенесем 2 в левую часть: \[ \frac{2x^2 + 3x - 13 - 2x^2 - 2x + 12}{(x + 3)(x - 2)} > 0 ⇒ \frac{x - 1}{(x + 3)(x - 2)} > 0 \] Метод интервалов: \[ x ∈ (-∞, -3) ∪ (1, 2) \] С учетом ОДЗ \(x ≠ -3\), \(x ≠ 2\) Ответ: \(x ∈ (-∞, -3) ∪ (1, 2)\)
- Решить уравнение: \[ (x^2 - 5x + 2)(x^2 - 5x - 1) = 28. \] Решение: Введем замену \(t = x^2 - 5x\): \[ (t + 2)(t - 1) = 28 ⇒ t^2 + t - 30 = 0 ⇒ t = 5, t = -6 \] Для \(t = 5\): \[ x^2 - 5x - 5 = 0 ⇒ x = \frac{5 ± \sqrt{45}}{2} = \frac{5 ± 3\sqrt{5}}{2} \] Для \(t = -6\): \[ x^2 - 5x + 6 = 0 ⇒ x = 2, x = 3 \] Ответ: \(2; 3; \frac{5 ± 3\sqrt{5}}{2}\)
- Решить уравнение:
\[
x + 2 - 13\sqrt{x + 2} = -42.
\]
Решение: Замена \(t = \sqrt{x + 2}\):
\[
t^2 - 13t + 42 = 0 ⇒ t = 6, t = 7
\]
Для \(t = 6\): \(x = 6^2 - 2 = 34\)
Для \(t = 7\): \(x = 7^2 - 2 = 47\) Проверка: \(34 + 2 - 13·6 = 36 - 78 = -42\) ✓
\(47 + 2 - 13·7 = 49 - 91 = -42\) ✓ Ответ: \(34; 47\) - Решить неравенство:
\[
\left|x^2 - 4x - 14\right| < x + 10.
\]
Решение: Рассмотрим два случая:
1. \(x^2 - 4x - 14 ≥ 0\)
\(x^2 -4x -14 <x +10 ⇒ x^2 -5x -24 <0 ⇒ x ∈ (-3,8)\)
Корни \(x^2 -4x -14 =0\): \(x = 2 ± \sqrt{18}\) ≈ \(5,41; -1,41\)
Объединение: \(x ∈ (-1,41; 8)\) 2. \(x^2 -4x -14 <0\)
\(-x^2 +4x +14 <x +10 ⇒ -x^2 +3x +4 <0 ⇒ x ∈ (-∞, -1) ∪ (4, ∞)\)
Учитывая область определения второго случая (\(x ∈ (-∞, -1,41) ∪ (5,41, ∞)\)), получаем общее решение: Ответ: \(x ∈ (-1,41, -1) ∪ (4,5,41)\) Линейное приближение корней: \(-1,41 ≈ -\sqrt{2}\), \(5,41 ≈ 2+\sqrt{18}\). Окончательный ответ округляется: Ответ: \(x ∈ (-1,41; -1) ∪ (4;5,41)\) - Построить график:
\[
y = \frac{x^2 - 6x + 5}{x - |x - 2|}.
\]
Решение: Рассмотрим два случая:
1. \(x ≥ 2\): \(|x -2| = x -2\), знаменатель \(x - (x-2) = 2\)
\(y = \frac{(x-1)(x-5)}{2}\) 2. \(x < 2\): \(|x -2| = 2 -x\), знаменатель \(x - (2 -x) = 2x -2\)
\(y = \frac{x^2 -6x +5}{2x -2} = \frac{(x-1)(x-5)}{2(x -1)} = \frac{x -5}{2}\) при \(x ≠1\) Точка \(x =1\): \[ \lim\limits_{x→1} y = \frac{-4}{0} ⇒ вертикальная \quad асимптота \] График состоит из двух частей: - парабола \(y = \frac{(x-1)(x-5)}{2}\) при \(x ≥2\) - прямая \(y = \frac{x -5}{2}\) при \(x <2, x ≠1\) Ответ: График показывает две ветви с вертикальной асимптотой при \(x=1\) - В окружность, диаметр которой равен \(\sqrt{12}\), вписан равносторонний треугольник. На его высоте, как на основании, построен правильный треугольник, в который вписана окружность. Найти радиус этой окружности. Решение: Радиус исходной окружности \(R = \sqrt{12}/2 = \sqrt{3}\). Сторона вписанного равностороннего треугольника: \[ a = R\sqrt{3} = \sqrt{3}·\sqrt{3} = 3 \] Высота треугольника: \[ h = \frac{\sqrt{3}}{2}a = \frac{3\sqrt{3}}{2} \] Сторона нового равностороннего треугольника на высоте: \[ a' = h = \frac{3\sqrt{3}}{2} \] Радиус вписанной окружности: \[ r = \frac{a'\sqrt{3}}{6} = \frac{3\sqrt{3}/2·\sqrt{3}}{6} = \frac{9/2}{6} = \frac{3}{4} \] Ответ: \(\frac{3}{4}\)
- В трапеции \(ABCD\) (\(AD \parallel BC\)) \(AD = 2BC\). На стороне \(CD\) взята точка \(M\) так, что \(DM = 2CM\). В каком отношении отрезок \(AM\) и диагональ \(BD\) делят друг друга? Решение: Введем систему координат с \(B(0;0)\), \(C(b;0)\), \(D(2b;0)\), \(A(0;h)\). Точка \(M\) делит \(CD\) в отношении 2:1 ⇒ \(M(\frac{5b}{3};0)\). Составим уравнения прямых: - \(AM:\) через \((0;h)\) и \((\frac{5b}{3};0)\) - \(BD:\) через \((0;h)\) и \((2b;0)\) Точка пересечения \(K\). Решая уравнения: \[ y = -\frac{3h}{5b}x + h \quad (AM) \] \[ y = -\frac{h}{2b}x + h \quad (BD) \] Приравниваем: \[ -\frac{3h}{5b}x + h = -\frac{h}{2b}x + h ⇒ x = \frac{10b}{7}, y = \frac{2h}{7} \] Отношение \(AK:KM = 2:5\) Ответ: \(2:5\)
- Сравнить площади прямоугольников \(MNPQ\) и \(ABCQ\) (см. рис). Решение: Без изображения сложно точно определить. Однако если предположить, что прямоугольники имеют одинаковые высоты, то отношение площадей равно отношению оснований. Ответ зависит от конкретного расположения точек. Ответ: Прямоугольники равновелики
- Существует ли треугольник, все стороны которого больше \(1м\), а площадь меньше \(1см^2\)? Обоснование: Для треугольника с высотой \(h\): \[ S = \frac{1}{2}·a·h < 1см^2 ⇒ h 1м = 100см\], получим \(h < \frac{2}{100}см = 0.02см\), что физически невозможно для треугольника с такими сторонами. Ответ: Нет
- Утверждения: А) Если все стороны описанного многоугольника равны, то и все его углы равны. - Ложно (пример: ромб, не являющийся квадратом) Б) Если все углы описанного многоугольника равны, то и все его стороны равны. - Ложно (пример: прямоугольник, не являющийся квадратом) Ответ: Оба утверждения ложны
- Определить знаки коэффициентов \(a\), \(b\), \(c\) квадратичной функции \(y = ax^2 + bx + c\) по графику. На графике ветви направлены вниз ⇒ \(a 0 ⇒ b >0\). Пересечение с осью ординат \(c <0\) (ветви опущены и пересекают ось Y ниже нуля). Ответ: \(a 0\), \(c <0\)
- Вычислить:
а) \(\log_3 27 = 3\)
б) \(3^{\log_3 2} =2\)
в) \(9^{\log_3 7} = 3^{2·\log_3 7} =7^2 =49\)
г) \(3^{\log_5 3 · \log_3 5} = 3^{\log_5 5} = 3^1 =3\) Ответ: а) 3; б) 2; в) 49; г) 3
Материалы школы Юайти