Лицей №239 из 9 в 10 класс 2005 год вариант 1
Печать
youit.school ©
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ № 239
2005 год
Вариант 1
- Упростить:
\[
(1 - a^2) : \left( \left( \frac{1 - a\sqrt{a}}{1 - \sqrt{a}} + \sqrt{a} \right) \cdot \left( \frac{1 + a\sqrt{a}}{1 + \sqrt{a}} - \sqrt{a} \right) \right) + 1.
\]
- Решить уравнение:
\[
\frac{1}{x^2 + 2x + 4} + \frac{1}{x - 2} = \frac{x^2 - 2x + 4}{x^3 - 8}.
\]
- Решить неравенство:
\[
\frac{(x + 1)(x + 2)}{x^2 + 7x + 12} \leq 1.
\]
- Решить уравнение:
\[
(x^2 + 3x + 1)(x^2 + 3x + 3) + 1 = 0.
\]
- Решить уравнение:
\[
x - 3 + 4\sqrt{x - 3} = 12.
\]
- Решить неравенство:
\[
\left|x^2 - 7x + 7\right| > x - 5.
\]
- Построить график:
\[
y = \frac{x^2 + 7x + 6}{x + |x + 2|}.
\]
- В окружность радиуса $\sqrt{12}$ вписан квадрат. На диагонали квадрата, как на основании, построен равносторонний треугольник, вокруг которого описана окружность. Найти радиус этой окружности.
- В треугольнике $ABC$ проведена медиана $BM$. На стороне $BC$ взята точка $N$ так, что $CN = 2BN$. В каком отношении $AN$ и $BM$ делят друг друга?
- Сравнить площади параллелограммов $ABCD$ и $AMNP$ (см. рис).
- Существует ли треугольник, две высоты которого больше $1м$, а площадь меньше $1см^2$? Не забудьте обосновать ответ.
- Даны два утверждения:
А) Если все стороны вписанного многоугольника равны, то и все его углы равны.
Б) Если все углы вписанного многоугольника равны, то и все его стороны равны.
Какое из этих утверждений верно, а какое нет? (Подсказка: рассмотрите четырехугольники и пятиугольники).
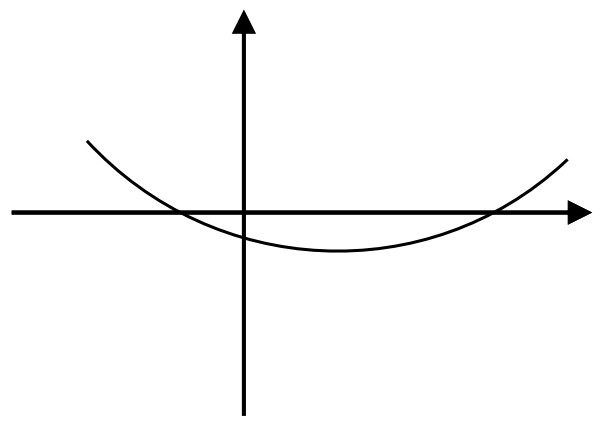
- Дано изображение графика функции $y = ax^2 + bx + c$ (см. рис.). Определить знаки коэффициентов $a$, $b$, $c$. Не забудьте обосновать ответ.
- Логарифмом числа $a > 0$ по основанию $2$ называется показатель степени, в которую нужно возвести $2$, чтобы получить $a$. Обозначение: $\log_2 a$.
Вычислить:
а) $\log_2 8$ ; $\quad$ б) $2^{\log_2 3}$ ; $\quad$ в) $4^{\log_2 5}$ ; $\quad$ г) Подумайте о том, что означает символ $\log_5 a$ и вычислите $2^{\log_5 3 \cdot \log_2 5}$
Материалы школы Юайти
youit.school ©
Решения задач
- Упростить:
\[
(1 - a^2) : \left( \left( \frac{1 - a\sqrt{a}}{1 - \sqrt{a}} + \sqrt{a} \right) \cdot \left( \frac{1 + a\sqrt{a}}{1 + \sqrt{a}} - \sqrt{a} \right) \right) + 1.
\]
Решение: Упростим выражения в скобках отдельно. Для первого слагаемого:
\[
\frac{1 - a\sqrt{a}}{1 - \sqrt{a}} + \sqrt{a} = (1 + \sqrt{a} + a) + \sqrt{a} = (1 + \sqrt{a})^2.
\]
Для второго слагаемого:
\[
\frac{1 + a\sqrt{a}}{1 + \sqrt{a}} - \sqrt{a} = (1 - \sqrt{a} + a) - \sqrt{a} = (1 - \sqrt{a})^2.
\]
Произведение упрощается:
\[
(1 + \sqrt{a})^2 \cdot (1 - \sqrt{a})^2 = (1 - a)^2.
\]
Исходное выражение:
\[
\frac{1 - a^2}{(1 - a)^2} + 1 = \frac{(1 - a)(1 + a)}{(1 - a)^2} + 1 = \frac{1 + a}{1 - a} + 1 = \frac{2}{1 - a}.
\]
Ответ: $\frac{2}{1 - a}$.
- Решить уравнение:
\[
\frac{1}{x^2 + 2x + 4} + \frac{1}{x - 2} = \frac{x^2 - 2x + 4}{x^3 - 8}.
\]
Решение: Учитывая, что $x^3 - 8 = (x - 2)(x^2 + 2x + 4)$, умножим обе части на $(x - 2)(x^2 + 2x + 4)$:
\[
(x - 2) + (x^2 + 2x + 4) = x^2 - 2x + 4.
\]
Левый член:
\[
x^2 + 3x + 2 = x^2 - 2x + 4 \quad \Rightarrow \quad 5x = 2 \quad \Rightarrow \quad x = \frac{2}{5}.
\]
Ответ: $x = \frac{2}{5}$.
- Решить неравенство:
\[
\frac{(x + 1)(x + 2)}{x^2 + 7x + 12} \leq 1.
\]
Решение: Преобразуем неравенство:
\[
\frac{-4x - 10}{(x + 3)(x + 4)} \leq 0 \quad \Rightarrow \quad \frac{4x + 10}{(x + 3)(x + 4)} \geq 0.
\]
Критические точки: $x = -\frac{5}{2},\; -4,\; -3$. Ответ:
\[
x \in (-4; -3) \cup \left[-\frac{5}{2}; +\infty\right).
\]
Ответ: $x \in (-4; -3) \cup \left[-\frac{5}{2}; +\infty\right)$.
- Решить уравнение:
\[
(x^2 + 3x + 1)(x^2 + 3x + 3) + 1 = 0.
\]
Решение: Замена $t = x^2 + 3x + 2$:
\[
(t - 1)(t + 1) + 1 = t^2 - 1 + 1 = t^2 = 0 \quad \Rightarrow \quad t = 0.
\]
Таким образом:
\[
x^2 + 3x + 2 = 0 \quad \Rightarrow \quad x = -1,\; x = -2.
\]
Ответ: $x = -2,\; -1$.
- Решить уравнение:
\[
x - 3 + 4\sqrt{x - 3} = 12.
\]
Решение: Замена $y = \sqrt{x - 3}$:
\[
y^2 + 4y - 12 = 0 \quad \Rightarrow \quad y = 2 \quad(y \neq -6).
\]
Тогда:
\[
x - 3 = 4 \quad \Rightarrow \quad x = 7.
\]
Ответ: $x = 7$.
- Решить неравенство:
\[
\left|x^2 - 7x + 7\right| > x - 5.
\]
Решение: \[При \quad x 0 \quad \cup \quad x^2 - 6x + 2 6 \quad \cup \quad 3 - \sqrt{7} < x < 3 + \sqrt{7}.
\]
Ответ: $x \in (-\infty; 3 + \sqrt{7}) \cup (6; +\infty)$.
- Построить график:
\[
y = \frac{x^2 + 7x + 6}{x + |x + 2|}.
\]
Решение: Разбиваем на случаи:
- При $x \geq -2$: $y = \frac{(x + 1)(x + 6)}{2(x + 1)} = \frac{x + 6}{2}$ (исключая $x = -1$).
- При $x < -2$: $y = \frac{(x + 1)(x + 6)}{-2}$ (парабола).
- Радиус окружности, описанной вокруг равностороннего треугольника с основанием-диагональю квадрата ($4\sqrt{3}$), равен:
\[
R = \frac{a}{\sqrt{3}} = \frac{4\sqrt{3}}{\sqrt{3}} = 4.
\]
Ответ: $4$.
- Отношение деления $AN$ и $BM$:
- С использованием координат и параметризации получаем:
- $BO:OM = 1:1$, $AO:ON = 3:1$.
- Сравнение площадей параллелограммов: Если параллелограммы имеют одинаковые основания и высоты, площади равны. Ответ: равны.
- Существует треугольник с двумя высотами >1 м и площадью <1 см²: Да. Пример: $h_1 = h_2 = 1.1$ м, $S = 0.0001$ м². Ответ: существует.
- Утверждения:
- А верно (вписанный с равными сторонами имеет равные углы),
- Б ложно (прямоугольник с равными углами $\neq$ квадрат).
- Знаки коэффициентов квадратичной функции:
- Ветви вверх → $a > 0$,
- Вершина слева от оси $Y$ → $b > 0$,
- Пересечение с $Y$ выше нуля → $c > 0$.
- Вычислить:
- а) $\log_2 8 = 3$,
- б) $2^{\log_2 3} = 3$,
- в) $4^{\log_2 5} = 25$,
- г) $2^{\log_5 3 \cdot \log_2 5} = 3$.
Материалы школы Юайти