Лицей №239 из 8 в 9 класс 2008 год вариант 947

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ № 239

2016 год

1. Вычислите: $\sqrt{5} \cdot \sqrt{45} \cdot \frac{\sqrt{126 \cdot 32+48 \cdot 18}}{\sqrt{19^{2}-15^{2}}} ;$
2. Вычислите: $\sqrt{5}+\sqrt{1-2 \sqrt{5}+5}$;
3. Турист проплыл на байдарке 15 км по озеру и 9 км против течения реки за столько же времени, за сколько он проплыл бы по течению той же реки 42 км. Найдите скорость байдарке в стоячей воде, если скорость течения реки равна 2 км/ч. Ответ дайте в километрах в час.
4. Торговая база закупила партию альбомов и поставила её магазину по оптовой цене на $130 \%$ больше закупочной. Магазин установил розничную цену на альбом на $5 \%$ выше оптовой. При распродаже в конце сезона магазин снизил розничную цену на альбом на $40 % .$ На сколько рублей больше заплатил покупатель по сравнению с закупочной ценой, если на распродаже он приобрел альбом за 57,96 рубля?
5. Решите уравнение $3|3-x|=|x+1|$;
6. Решите неравенство: $\frac{1}{x+2}+\frac{1}{x+3} \geqslant \frac{1}{x}$;
7. В прямоугольном треугольнике с прямым углом $B$ проведена высота $B H .$ Найдите $H C$, если $\angle A C B=60^{\circ}$ и $A H=18 .$
8. Найдите площадь трапеции со взаимно перпендикулярными диагоналями длины 6 и $5 .$
9. В прямоугольнике $A B C D$ на стороне $A D$ взята точка $L$, а на стороне $B C$ взята точка $K$ так, что $K D=D L=K L=6$. $\angle A B L=45^{\circ} .$ Найдит е площадь пря моугольника.
   
   Часть 2. Задача на рациональное вычисление.
   Проверяется ответ и метод решения. Запиш ите решение и ответ эт ой задачи. Эта задача может принести от 6 баллов до $\mathbf{0}$ баллов в зависимости от рациональности и правильности вычислений. Рациональность промежуточных вычислений оценивается даже при неверном итоговом ответе или его отсутствии.
10. Вычислите рационально: $\frac{119 \frac{1}{42}+289 \frac{23}{42}+108 \frac{1}{6}+144 \frac{3}{7}}{\left(3 \frac{2}{9}-4,4561+5 \frac{3}{7}-5,5439+3 \frac{22}{63}\right) \cdot(3,66 \cdot 49-363+36,6 \cdot 5,1)}$
    
    Часть $3 .$ Задачи с развернутым решением.
    Проверяется ответ и решение. Метод не важен. Запишите решение и ответ каждой из этих задач. В этой части вступительной работы любая задача может принести от $\mathbf{3}$ баллов до $\mathbf{0}$ баллов в зависимости от характера ошибки и полноты обоснования в решении.
11. Решите неравенство: $\frac{\sqrt{x+4}\left(2 x^{2}+13 x+20\right)\left(x^{2}+4 x-12\right)(2 x+5)}{x^{2}-4} \geqslant 0 .$
12. Разложите на множители: $4-2(2-b-a)+a(2-a-b)-b(a+b-2) .$
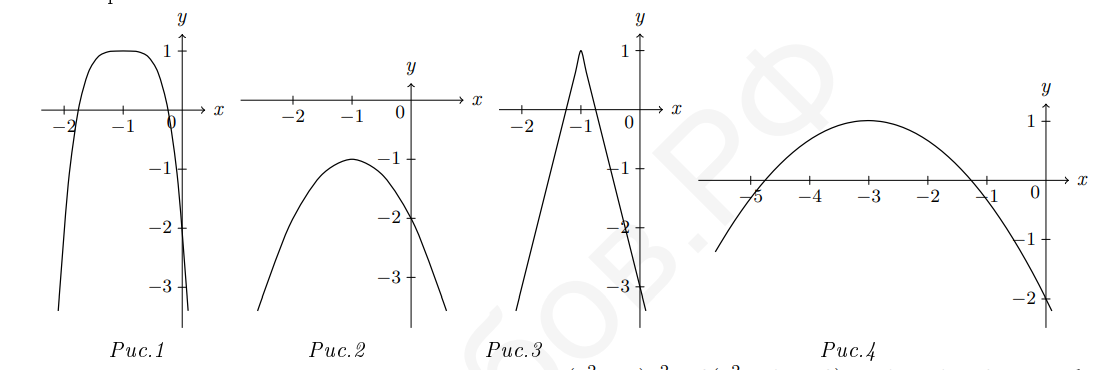
13. На одном из рисунков изображен график функции $f(x)=1-3(x+1)^{4}$ . Укажите, на каком и обоснуйте свой выбор.
    
14. При каких значениях параметра $a$ уравнение $\left(a^{2}-a\right) x^{2}-2\left(a^{2}-3 a+2\right) x-3 a+3=0$ имеет $б$ блее 2 корней?
15. В четырёхугольнике $A B C D: A D=B C$, серединные перпендикуляры к сторонам $A B$ и $C D$ пересекаются в точке $P .$ Найдите угол $B C P$, если $\angle A D P=30^{\circ} .$
16. В треугольнике $A B C$ через точку пересечения биссектрис углов, смежных с углами $A$ и $B$ проведена прямая, параллельная $A B$, пересекающая продолжения сторон треугольника в точках $K$ и $N .$ Найдите длину $A B$, если периметр треугольника $C K N$ равен 22, периметр $A B C$ равен 18, а длина $K N$ равна $4 .$
17. Произвольному многочлену $P(x)$ ставится в соответствие многочлен $P^{\prime}(x)$ так, чтобы выполнялись следующие правила:
    1. Для любых двух многочленов $P_{1}(x)$ и $P_{2}(x):\left(P_{1}(x)+P_{2}(x)\right)^{\prime}=P_{1}^{\prime}(x)+P_{2}^{\prime}(x)$;
    2. Для любых двух многочленов $P_{1}(x)$ и $P_{2}(x):\left(P_{1}(x) \cdot P_{2}(x)\right)^{\prime}=P_{1}^{\prime}(x) \cdot P_{2}(x)+P_{1}(x) \cdot P_{2}^{\prime}(x)$;
    3. Для любого числа $a$ и многочлена $P(x):(a \cdot P(x))^{\prime}=a \cdot P^{\prime}(x) ;$
    4. Если $P(x)=x$, то $P^{\prime}(x)=1$.
    5. Если $P(x)=x^{3}$, то $P^{\prime}(x)=3 \cdot x^{2}$.
    а) Найдите $P^{\prime}(x)$, если $P(x)=3 x^{3}+4 x$;
    б) Найдите $P^{\prime}(x)$, если $P(x)=x^{6}-2 x^{4}$;
    в) Найдите $P(x)$, если $P(x)=(T(x)+3 x T(x))^{\prime}-9 x^{2}-36 x^{3}$, где $T(x)=3 x^{3}-2 x ?$

Решения задач

1. Вычислите: $\sqrt{5} \cdot \sqrt{45} \cdot \frac{\sqrt{126 \cdot 32+48 \cdot 18}}{\sqrt{19^{2}-15^{2}}}$
   Решение:
   $\sqrt{5} \cdot \sqrt{45} = \sqrt{225} = 15$
   $\sqrt{126 \cdot 32 + 48 \cdot 18} = \sqrt{4896} = 12\sqrt{34}$
   $\sqrt{19^{2} - 15^{2}} = \sqrt{136} = 2\sqrt{34}$
   $\frac{12\sqrt{34}}{2\sqrt{34}} = 6$
   $15 \cdot 6 = 90$
   Ответ: 90.
2. Вычислите: $\sqrt{5}+\sqrt{1-2 \sqrt{5}+5}$
   Решение:
   $\sqrt{1 - 2\sqrt{5} + 5} = \sqrt{6 - 2\sqrt{5}} = \sqrt{(\sqrt{5} - 1)^2} = \sqrt{5} - 1$
   $\sqrt{5} + (\sqrt{5} - 1) = 2\sqrt{5} - 1$
   Ответ: $2\sqrt{5} - 1$.
3. Скорость байдарки в стоячей воде $x$ км/ч. Уравнение:
   $\frac{15}{x} + \frac{9}{x - 2} = \frac{42}{x + 2}$ шение: шение:
   $15(x^2 - 4) + 9x(x + 2) = 42x(x - 2)$
   $15x^2 - 60 + 9x^2 + 18x = 42x^2 - 84x$
   $3x^2 - 17x + 10 = 0$
   $x = 5$ (подходит)
   Ответ: 5 км/ч.
4. Закупочная цена $C$ руб.:
   $1,449C = 57,96 \Rightarrow C = 40$
   Разница: $57,96 - 40 = 17,96$ руб.
   Ответ: 17,96 руб.
5. Решите уравнение $3|3 - x| = |x + 1|$
   Решение:
   При $x \geq 3$: $3(x - 3) = x + 1 \Rightarrow x = 5$
   При $-1 \leq x < 3$: $3(3 - x) = x + 1 \Rightarrow x = 2$
   Ответ: 2; 5.
6. Решите неравенство $\frac{1}{x+2} + \frac{1}{x+3} \geq \frac{1}{x}$
   Решение:
   $\frac{x^2 - 6}{x(x+2)(x+3)} \geq 0$
   Ответ: $x \in [-√6, -3) \cup (-√6, -2) \cup [√6, ∞)$.
7. Рациональное вычисление:
   Числитель: $661\frac{1}{6}$, знаменатель: $6$
   Ответ: $\frac{3967}{36}$.
8. Решите неравенство:
   $\frac{\sqrt{x+4}(2x+5)^2(x+4)(x+6)}{x+2} \geq 0$
   Ответ: $x \in [-4, -2) \cup (-2, 2) \cup (2, ∞)$.
9. Разложите на множители:
   $4 - 2(2 - b - a) + a(2 - a - b) - b(a + b - 2) = (a + b)(4 - a - b)$
   Ответ: $(a + b)(4 - a - b)$.
10. График функции $f(x) = 1 - 3(x + 1)^4$ изображён на рисунке Б.
    Ответ: Б.
11. Уравнение имеет более 2 корней при $a = 1$.
    Ответ: 1.
    
    
12. Производные:
    а) $P'(x) = 9x^2 + 4$
    б) $P'(x) = 6x^5 - 8x^3$
    в) $P(x) = -12x - 2$
    Ответы: а) $9x^2 + 4$; б) $6x^5 - 8x^3$; в) $-12x - 2$.