8 800 707 6729
8 800 707 6729Telegram канал

Лицей №239 из 8 в 9 класс 2003 год вариант 2

Сложность:
Дата экзамена: 2003
Печать
youit.school ©

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ № 239


2003 год


Вариант 2



  1. Упростить: \[ \frac{a - 1}{a^4 - a^3 + a^2} \;:\; \frac{1}{a^5 + a^2}. \]
  2. Разложить на множители: \[ a^3 + 3a - 4. \]
  3. Вычислить: \[ \sqrt{7 + 2\sqrt{6}}\;-\;\sqrt{7 - 2\sqrt{6}}. \]
  4. Положительное число \(a\) составляет 400 % от своего квадрата. Найти число \(a\).
  5. Решить в целых числах уравнение: \[ (x + 2)\,(y - 3) = 2. \]
  6. При каких целых \(n\) число \[ \frac{4n + 5}{2n + 1} \] является целым?
  7. Решить уравнение: \[ \lvert 2x + 9\rvert = x. \]
  8. Решить неравенство: \[ \lvert x - 3\rvert \;-\;\lvert 2x + 4\rvert < 5. \]
  9. Построить график функции: \[ y = \frac{x^2 + 5x + 6}{\lvert x + 2\rvert}. \]
  10. Решить уравнение: \[ \frac{1}{x + 4} + \frac{1}{x + 2} + \frac{1}{x - 4} + \frac{1}{x - 2} = 0. \]
  11. Решить неравенство: \[ \frac{x^2}{x - 1} \le 4. \]
  12. Решить уравнение: \[ (x + 1)^4 - x^2 - 2x - 13 = 0. \]
  13. При каких \(k\) уравнение \[ (k + 2)x^2 + 2(k + 1)x + k = 0 \] имеет единственный корень?
  14. Угол, противолежащий основанию равнобедренного треугольника, равен \(120^\circ\). Основание равно 8 см. Найти длину высоты, проведённой к боковой стороне.
  15. Найти площадь прямоугольной трапеции, у которой две меньшие стороны равны 4 см, а меньший угол при основании равен \(45^\circ\).
  16. Найти углы ромба, если его диагонали равны \(4\sqrt{3}\) и \(4\).
  17. К окружности проведены касательная и секущая, проходящая через центр окружности. Длина касательной в три раза меньше длины секущей. Найти отношение длины радиуса окружности к длине касательной.
  18. Точка \(M\) лежит на стороне \(BC\) параллелограмма \(ABCD\), причём \(BM:MC = 3:1\). Выразить вектор \(\overrightarrow{MD}\) через векторы \(\overrightarrow{AD}\) и \(\overrightarrow{AB}\).
  19. Сколько различных диагоналей можно провести в выпуклом восьмиугольнике?
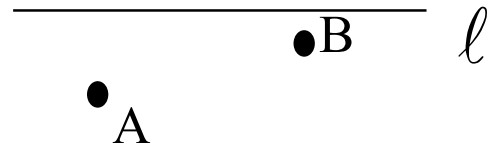
  20. На прямой \(\ell\) найти точку \(C\), чтобы сумма расстояний \(AC + BC\) была наименьшей.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Упростить: \[ \frac{a - 1}{a^4 - a^3 + a^2} : \frac{1}{a^5 + a^2} \] Решение: \[ \frac{a - 1}{a^2(a^2 - a + 1)} \cdot (a^5 + a^2) = \frac{(a - 1)a^2(a^3 + 1)}{a^2(a^2 - a + 1)} = (a - 1)(a + 1) = a^2 - 1 \] Ответ: \( a^2 - 1 \).
  2. Разложить на множители: \[ a^3 + 3a - 4 \] Решение: Подстановка \( a = 1 \) даёт корень: \[ (a - 1)(a^2 + a + 4) \] Ответ: \( (a - 1)(a^2 + a + 4) \).
  3. Вычислить: \[ \sqrt{7 + 2\sqrt{6}} - \sqrt{7 - 2\sqrt{6}} \] Решение: Заметим, что \( \sqrt{7 + 2\sqrt{6}} = \sqrt{6} + 1 \) и \( \sqrt{7 - 2\sqrt{6}} = \sqrt{6} - 1 \), тогда: \[ (\sqrt{6} + 1) - (\sqrt{6} - 1) = 2 \] Ответ: 2.
  4. Найти число \( a \): \[ a = 400% \text{ от } a^2 \quad \Rightarrow \quad a = 4a^2 \quad \Rightarrow \quad a = \frac{1}{4} \] Ответ: \( \frac{1}{4} \).
  5. Решить уравнение в целых числах: \[ (x + 2)(y - 3) = 2 \] Решение: Пары множителей: \( (1, 2) \), \( (2, 1) \), \( (-1, -2) \), \( (-2, -1) \). Получаем решения: \[ (-1, 5),\ (0, 4),\ (-3, 1),\ (-4, 2) \] Ответ: \( (-1, 5)\), \( (0, 4)\), \( (-3, 1)\), \( (-4, 2) \).
  6. Найти целые \( n \): \[ \frac{4n + 5}{2n + 1} \in \mathbb{Z} \] Решение: Выделяем целую часть: \[ 2 + \frac{3}{2n + 1} \quad \Rightarrow \quad 2n + 1 \in \{\pm1, \pm3\} \] Ответ: \( n = -2,\ -1,\ 0,\ 1 \).
  7. Решить уравнение: \[ |2x + 9| = x \] Решение: Первый случай: \( 2x + 9 = x \Rightarrow x = -9 \) — не подходит. Второй случай: \( 2x + 9 = -x \Rightarrow x = -3 \) — не подходит. Ответ: нет решений.
  8. Решить неравенство: \[ |x - 3| - |2x + 4| < 5 \] Рассмотрим три интервала:
    • \( x < -2 \): \( -x -2 < 5 \) — верно для всех \( x < -2 \).
    • \( -2 \le x < 3 \): \( -3x -1 < 5 \) — верно для всех \( -2 \le x < 3 \).
    • \( x \ge 3 \): \( -x -7 < 5 \) — верно для всех \( x \ge 3 \).
    Ответ: \( x \in \mathbb{R} \).
  9. Построить график функции: \[ y = \frac{x^2 + 5x + 6}{|x + 2|} \] Решение: Упростим: \[ y = \begin{cases} x + 3, & x > -2 \\ -x - 3, & x < -2 \end{cases} \] Вертикальная асимптота при \( x = -2 \). Ответ: две прямые ветви.
  10. Решить уравнение: \[ \frac{1}{x + 4} + \frac{1}{x + 2} + \frac{1}{x - 4} + \frac{1}{x - 2} = 0 \] Решение: Общий знаменатель: \( (x^2 -16)(x^2 -4) \). Уравнение приводится к: \[ 4x(x^2 - 10) = 0 \quad \Rightarrow \quad x = 0,\; x = \pm\sqrt{10} \] Ответ: \( 0,\ \pm\sqrt{10} \).
  11. Решить неравенство: \[ \frac{x^2}{x - 1} \le 4 \] Решение: Приведём к виду: \[ \frac{(x - 2)^2}{x - 1} \le 0 \] Решение: \( x < 1 \) или \( x = 2 \). Ответ: \( x \in (-\infty; 1) \cup \{2\} \).
  12. Решить уравнение: \[ (x + 1)^4 - x^2 - 2x - 13 = 0 \] Решение: После преобразований: \[ (x - 1)(x + 3)(x^2 + 2x + 4) = 0 \quad \Rightarrow \quad x = 1,\; x = -3 \] Ответ: \( 1,\ -3 \).
  13. Найти \( k \): \[ (k + 2)x^2 + 2(k + 1)x + k = 0 \] Условие единственного корня: Либо \( k + 2 = 0 \) (линейное уравнение), либо дискриминант равен нулю: \[ k = -2 \] Ответ: \( k = -2 \).
  14. Найти длину высоты равнобедренного треугольника: Основание \( 8 \) см, угол при вершине \( 120^\circ \). Высота к боковой стороне вычисляется через площадь: \[ S = \frac{1}{2} \cdot 8 \cdot 4 \cdot \sin 60^\circ = 16\sqrt{3} \quad \Rightarrow \quad h = \frac{2S}{8/\sqrt{3}} = 4 \text{ см} \] Ответ: \( 4 \) см.
  15. Найти площадь прямоугольной трапеции: Меньшие стороны \( 4 \) см, угол \( 45^\circ \). Площадь равна сумме оснований, умноженной на высоту: \[ S = (4 + 8) \cdot 4 / 2 = 24 \text{ см}^2 \] Ответ: \( 24 \) см².
  16. Найти углы ромба: Диагонали \( 4\sqrt{3} \) и \( 4 \). Углы вычисляются через арктангенс: \[ \tan \alpha = \frac{4\sqrt{3}}{4} = \sqrt{3} \quad \Rightarrow \quad \alpha = 60^\circ,\ 120^\circ \] Ответ: \( 60^\circ,\ 120^\circ \).
  17. Отношение радиуса к длине касательной: Используя теорему о секущей и касательной: \[ L^2 = 3L \cdot (3L - 2R) \quad \Rightarrow \quad \frac{R}{L} = \frac{4}{3} \] Ответ: \( \frac{4}{3} \).
  18. Выразить вектор \( \overrightarrow{MD} \): В параллелограмме \( ABCD \): \[ \overrightarrow{MD} = \frac{1}{4}\overrightarrow{AD} \] Ответ: \( \frac{1}{4}\overrightarrow{AD} \).
  19. Количество диагоналей в восьмиугольнике: Формула: \[ \frac{n(n - 3)}{2} = \frac{8 \cdot 5}{2} = 20 \] Ответ: 20.
  20. Точка \( C \) на прямой \( \ell \): Применить метод отражения для нахождения минимальной суммы расстояний. Ответ: точка пересечения прямой \( AB' \), где \( B' \) — отражение точки \( B \).
Материалы школы Юайти