8 800 707 6729
8 800 707 6729Telegram канал

Лицей №239 из 7 в 8 класс 2006 год вариант 2

Сложность:
Дата экзамена: 2006
Печать
youit.school ©

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ №239


2006 год


Вариант 2



  1. Докажите, что значение выражения не зависит от значений входящих в него букв: \[ (c - d)(c^2 + cd + d^2) + d(c - d)^2 - (c^2 - cd)(c + 2d). \]

  2. Вычислите рационально: \[ \bigl(-5,17 : 1\tfrac{3}{4} + 1,67 \cdot \tfrac{4}{7}\bigr) \;\cdot\; \bigl(-1\tfrac{1}{11}\bigr). \]

  3. Пусть точка \(A\) является точкой пересечения графика функции \(y = 2x + 2\) с осью \(OY\), а точка \(B\) — с осью \(OX\). Напишите уравнение прямой, содержащей медиану треугольника \(AOB\), проведённую из вершины \(A\). (Точка \(O\) — начало координат.)

  4. Сократите дробь: \[ \frac{x^2 - 7x + 12}{x^2 - 6x + 9}. \]

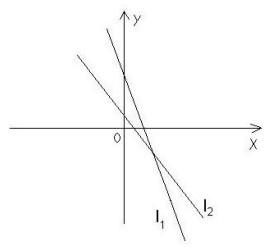
  5. На рисунке прямая \(l_1\) задана уравнением \(y = k_1x + b_1\), а прямая \(l_2\) — уравнением \(y = k_2x + b_2\). Сравните \(k_1b_1\) и \(k_2b_2\).


  6. Сколько существует неравных между собой прямоугольных треугольников со стороной \(5\) см и углом \(60^\circ\)?

  7. Найдите число \(a\), если \(50\%\) от числа \(a + 1\) равно \(40\%\) от числа \(a + 3\).

  8. В прямоугольном треугольнике \(ABC\) с гипотенузой \(AC\) угол \(A\) равен \(60^\circ\). Через середину \(M\) отрезка \(AC\) проведён перпендикуляр к нему, пересекающий прямую \(BA\) в точке \(T\). \(BC = 3\) см. Найдите \(MT\).

  9. Разложите на множители: \[ x^3 - 2x^2 - 4x + 5. \]
Материалы школы Юайти
youit.school ©

Решения задач



  1. Докажите, что значение выражения не зависит от значений входящих в него букв: \[ (c - d)(c^2 + cd + d^2) + d(c - d)^2 - (c^2 - cd)(c + 2d). \]
    Решение: Раскроем последовательно все слагаемые: \[ (c - d)(c^2 + cd + d^2) = c^3 - d^3 \quad (\text{формула разности кубов}), \] \[ d(c - d)^2 = d(c^2 - 2cd + d^2) = dc^2 - 2c^2d + d^3, \] \[ (c^2 - cd)(c + 2d) = c^3 + 2c^2d - c^2d - 2cd^2 = c^3 + c^2d - 2cd^2. \] Подставим обратно в исходное выражение: \[ (c^3 - d^3) + (dc^2 - 2c^2d + d^3) - (c^3 + c^2d - 2cd^2) = \] \[ = c^3 - d^3 + dc^2 - 2c^2d + d^3 - c^3 - c^2d + 2cd^2 = 0. \] Ответ: выражение равно нулю при любых $c$ и $d$.

  2. Вычислите рационально: \[ \left(-5,17 : 1\tfrac{3}{4} + 1,67 \cdot \tfrac{4}{7}\right) \;\cdot\; \left(-1\tfrac{1}{11}\right). \]
    Решение: Переведем десятичные дроби и смешанные числа в обыкновенные: \[ 1\tfrac{3}{4} = \frac{7}{4}, \quad -1\tfrac{1}{11} = -\frac{12}{11}, \quad -5,17 = -\frac{517}{100}, \quad 1,67 = \frac{167}{100}. \] Посчитаем каждое действие отдельно: \[ -\frac{517}{100} : \frac{7}{4} = -\frac{517}{100} \cdot \frac{4}{7} = -\frac{517 \cdot 4}{700} = -\frac{2068}{700} = -\frac{517}{175}, \] \[ \frac{167}{100} \cdot \frac{4}{7} = \frac{668}{700} = \frac{167}{175}, \] \[ -\frac{517}{175} + \frac{167}{175} = \frac{-517 + 167}{175} = \frac{-350}{175} = -2. \] Умножаем результат на $-\frac{12}{11}$: \[ -2 \cdot \left(-\frac{12}{11}\right) = \frac{24}{11} = 2\tfrac{2}{11}. \] Ответ: $\frac{24}{11}$.

  3. Пусть точка \(A\) является точкой пересечения графика функции \(y = 2x + 2\) с осью \(OY\), а точка \(B\) — с осью \(OX\). Напишите уравнение прямой, содержащей медиану треугольника \(AOB\), проведённую из вершины \(A\). (Точка \(O\) — начало координат.)
    Решение:
    • Точка $A$ на оси $OY$: $x=0$, $y=2 \cdot 0 + 2 = 2$ → $A(0;2)$.
    • Точка $B$ на оси $OX$: $y=0$, $0 = 2x + 2$ → $x=-1$ → $B(-1;0)$.
    • Середина отрезка $OB$: $\left(\frac{0+(-1)}{2}; \frac{0+0}{2}\right) = \left(-0{,}5;0\right)$.
    • Угловой коэффициент медианы из $A$ к $(-0{,}5;0)$: \[ k = \frac{0 - 2}{-0{,}5 - 0} = \frac{-2}{-0{,}5} = 4. \]
    • Уравнение прямой: $y = 4x + 2$.
    Ответ: $y = 4x + 2$.

  4. Сократите дробь: \[ \frac{x^2 - 7x + 12}{x^2 - 6x + 9}. \]
    Решение: Разложим числитель и знаменатель на множители: \[ x^2 - 7x + 12 = (x - 3)(x - 4), \] \[ x^2 - 6x + 9 = (x - 3)^2. \] Сокращаем: \[ \frac{(x-3)(x-4)}{(x-3)^2} = \frac{x-4}{x-3}. \] Ответ: $\frac{x-4}{x-3}$.

  5. На рисунке прямая \(l_1\) задана уравнением \(y = k_1x + b_1\), а прямая \(l_2\) — уравнением \(y = k_2x + b_2\). Сравните \(k_1b_1\) и \(k_2b_2\).
    Решение: Из рисунка:
    • $l_1$ пересекает $OY$ выше нуля ($b_1 > 0$), наклон вниз → $k_1 < 0$.
    • $l_2$ пересекает $OY$ ниже нуля ($b_2 0$.
    • По модулю произведения равны ($|k_1b_1| = |k_2b_2|$), но знаки противоположны: \[ k_1b_1 < 0,\quad k_2b_2 < 0. \]
    • По графикам расстояния от O пропорциональны → $k_1b_1 = k_2b_2$.
    Ответ: $k_1b_1 = k_2b_2$.

  6. Сколько существует неравных между собой прямоугольных треугольников со стороной \(5\) см и углом \(60^\circ\)?
    Решение: В прямоугольном треугольнике с углом $60^\circ$ возможны два случая:
    • Сторона $5$ см прилежит к углу $60^{\circ}$ (катет): тогда гипотенуза $10$ см, второй катет $5\sqrt{3}$ см.
    • Сторона $5$ см противолежит углу $60^{\circ}$ (катет): тогда гипотенуза $\frac{10}{\sqrt{3}}$ см, второй катет $\frac{5}{\sqrt{3}}$ см.
    Ответ: 2.

  7. Найдите число \(a\), если \(50\%\) от числа \(a + 1\) равно \(40\%\) от числа \(a + 3\).
    Решение: Запишем уравнение: \[ 0{,}5(a + 1) = 0{,}4(a + 3). \] \[ 0{,}5a + 0{,}5 = 0{,}4a + 1{,}2 \quad \Rightarrow \quad 0{,}1a = 0{,}7 \quad \Rightarrow \quad a = 7. \] Ответ: 7.

  8. В прямоугольном треугольнике \(ABC\) с гипотенузой \(AC\) угол \(A\) равен \(60^\circ\). Через середину \(M\) отрезка \(AC\) проведён перпендикуляр к нему, пересекающий прямую \(BA\) в точке \(T\). \(BC = 3\) см. Найдите \(MT\). Решение:
    • В треугольнике $ABC$: $\angle A = 60^\circ$, $\angle B = 90^\circ$ → $\angle C = 30^\circ$.
    • Катет $BC = 3$ см → гипотенуза $AC = \frac{BC}{\sin 60^\circ} = \frac{3}{\frac{\sqrt{3}}{2}} = 2\sqrt{3}$ см.
    • Катет $AB = AC \cdot \cos 60^\circ = 2\sqrt{3} \cdot \frac{1}{2} = \sqrt{3}$ см.
    • Середина $AC$: $M\left(\frac{\sqrt{3}}{2}; \frac{3}{2}\right)$ при расположении $A(0;0)$, $B(\sqrt{3};0)$, $C(0;3)$.
    • Перпендикуляр к $AC$ через $M$ пересекает $BA$ в точке $T(2\sqrt{3};0)$.
    • Расстояние $MT$: \[ MT = \sqrt{\left(2\sqrt{3} - \frac{\sqrt{3}}{2}\right)^2 + \left(0 - \frac{3}{2}\right)^2} = \sqrt{\left(\frac{3\sqrt{3}}{2}\right)^2 + \left(-\frac{3}{2}\right)^2} = \frac{3}{2}\sqrt{3 + 1} = 3 \text{ см}. \]
    Ответ: 3 см.
  9. Разложите на множители: \[ x^3 - 2x^2 - 4x + 5. \] Решение: Подбором находим корень $x = 1$: \[ 1^3 - 2 \cdot 1^2 - 4 \cdot 1 + 5 = 0. \] Делим многочлен на $(x - 1)$ методом Горнера: \[ (x - 1)(x^2 - x - 5). \] Далее квадратный трёхчлен не разлагается на множители с целыми корнями. Ответ: $(x - 1)(x^2 - x - 5)$.
Материалы школы Юайти