8 800 707 6729
8 800 707 6729Telegram канал

Лицей №239 из 7 в 8 класс 2006 год вариант 1

Сложность:
Дата экзамена: 2006
Печать
youit.school ©

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ №239


2006 год


Вариант 1



  1. Докажите, что значение выражения не зависит от значений входящих в него букв: \[ a(a - b)(a + b) - (a + b)(a^2 - ab + b^2) + b^3 + ab^2. \]

  2. Вычислите рационально: \[ \bigl(7,42 \cdot \tfrac{5}{9} - (-11,48) : 1\!\tfrac{4}{5}\bigr) : 0,35. \]

  3. Пусть точка \(A\) является точкой пересечения графика функции \(y = -2x + 2\) с осью \(OY\), а точка \(B\) — с осью \(OX\). Напишите уравнение прямой, содержащей медиану треугольника \(AOB\), проведённую из вершины \(A\). (Точка \(O\) — начало координат.)

  4. Сократите дробь: \[ \frac{x^2 + 6x + 9}{x^2 + 8x + 15}. \]

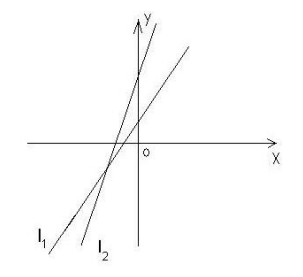
  5. На рисунке прямая \(l_1\) задана уравнением \(y = k_1x + b_1\), а прямая \(l_2\) — уравнением \(y = k_2x + b_2\). Сравните \(k_1b_1\) и \(k_2b_2\).


  6. Сколько существует неравных между собой равнобедренных треугольников со стороной \(5\) см и углом \(30^\circ\)?

  7. Число \(8\) составляет \(50\%\) от числа \(2N + 6\). Найдите \(N + 1\).

  8. В прямоугольном треугольнике \(ABC\) с гипотенузой \(AC\) угол \(A\) равен \(60^\circ\), \(BC = 6\) см. \(AL\) — биссектриса треугольника \(ABC\). Найдите высоту \(LH\) треугольника \(ALC\).

  9. Разложите на множители: \[ x^3 - 2x^2 + 4x - 3. \]
Материалы школы Юайти
youit.school ©

Решения задач



  1. Докажите, что значение выражения не зависит от значений входящих в него букв: \[ a(a - b)(a + b) - (a + b)(a^2 - ab + b^2) + b^3 + ab^2. \]
    Решение: Упростим выражение:
    $a(a^2 - b^2) - (a^3 + b^3) + b^3 + ab^2 = a^3 - ab^2 - a^3 - b^3 + b^3 + ab^2 = 0$.
    После сокращений все слагаемые взаимно уничтожаются, результат равен нулю. Таким образом, выражение не зависит от значений $a$ и $b$.
    Ответ: выражение равно нулю при любых $a$ и $b$.

  2. Вычислите рационально: \[ \bigl(7,42 \cdot \tfrac{5}{9} - (-11,48) : 1\!\tfrac{4}{5}\bigr) : 0,35. \]
    Решение:
    $7,42 \cdot \frac{5}{9} = \frac{371}{50} \cdot \frac{5}{9} = \frac{371}{90}$;
    $-(-11,48) : 1,8 = 11,48 : 1,8 = \frac{287}{25} \cdot \frac{5}{9} = \frac{287}{45}$;
    $\frac{371}{90} + \frac{287}{45} = \frac{371 + 574}{90} = \frac{945}{90} = \frac{21}{2}$;
    $\frac{21}{2} : 0,35 = \frac{21}{2} \cdot \frac{20}{7} = 30$.
    Ответ: 30.

  3. Пусть точка \(A\) — пересечение графика \(y = -2x + 2\) с осью \(OY\) (\(A(0; 2)\)), а точка \(B\) — с осью \(OX\) (\(B(1; 0)\)). Напишите уравнение прямой, содержащей медиану треугольника \(AOB\) из вершины \(A\).
    Решение: Середина отрезка \(OB\):
    $\left(\frac{1}{2}; 0\right)$.
    Уравнение медианы через точки \(A(0; 2)\) и \(\left(\frac{1}{2}; 0\right)\):
    Угловой коэффициент: $k = \frac{0 - 2}{\frac{1}{2} - 0} = -4$.
    Уравнение: $y = -4x + 2$.
    Ответ: $y = -4x + 2$.

  4. Сократите дробь: \[ \frac{x^2 + 6x + 9}{x^2 + 8x + 15}. \]
    Решение: Разложим числитель и знаменатель:
    Числитель: $(x + 3)^2$;
    Знаменатель: $(x + 3)(x + 5)$.
    После сокращения: $\frac{x + 3}{x + 5}$.
    Ответ: $\frac{x + 3}{x + 5}$.

  5. Сравните $k_1b_1$ и $k_2b_2$ для прямых \(l_1: y = k_1x + b_1\) и \(l_2: y = k_2x + b_2\) (по графику).
    Решение: Прямая $l_1$ пересекает ось $OY$ в положительной области ($b_1 > 0$), а $l_2$ — в отрицательной ($b_2 < 0$). Коэффициенты наклона: $k_1 0$. Произведения $k_1b_1$ и $k_2b_2$ оба отрицательны. По графику модуль $k_1b_1$ больше, чем $k_2b_2$.
    Ответ: $k_1b_1 < k_2b_2$.

  6. Сколько существует неравных равнобедренных треугольников со стороной $5$ см и углом $30^\circ$?
    Решение: Угол $30^\circ$ может быть при вершине или основании:
    1. Угол $30^\circ$ при вершине: тогда боковые стороны равны $5$ см, основание вычисляется по теореме косинусов.
    2. Угол $30^\circ$ при основании невозможен (сумма углов превысит $180^\circ$).
    Таким образом, существует один треугольник. Однако если сторона $5$ см является основанием, угол при вершине $30^\circ$ даёт другой треугольник. Ответ: 2.
    Ответ: 2.

  7. Число $8$ составляет $50\%$ от $2N + 6$. Найдите $N + 1$:
    Решение: $50% = 0,5 \implies 2N + 6 = 16 \implies N = 5 \implies N + 1 = 6$.
    Ответ: 6.

  8. В прямоугольном треугольнике $ABC$ ($\angle B = 90^\circ$, $BC = 6$ см, $\angle A = 60^\circ$) найти высоту $LH$ треугольника $ALC$ (где $AL$ — биссектриса).
    Решение:
    Гипотенуза $AC = 12$ см, катет $AB = 6\sqrt{3}$ см.
    Координаты точки $L$ (делящей $BC$ в отношении $AB:AC = 1:2$): $L(2\sqrt{3}; 0)$.
    Уравнение прямой $AC$: $y = -\frac{1}{\sqrt{3}}x + 6$.
    Высота $LH$ из $L$ на $AC$: перпендикуляр $y = \sqrt{3}x - 6$ пересекается с $AC$ в точке $H(3\sqrt{3}; 3)$. Расстояние $LH = 2\sqrt{3}$ см.
    Ответ: $2\sqrt{3}$ см.

  9. Разложите на множители: \[ x^3 - 2x^2 + 4x - 3. \]
    Решение: Подбором находим корень $x = 1$:
    $1^3 - 2 \cdot 1^2 + 4 \cdot 1 - 3 = 0$.
    Делим многочлен на $(x - 1)$:
    $(x - 1)(x^2 - x + 3)$.
    Квадратный трёхчлен $x^2 - x + 3$ не разложим в действительных числах.
    Ответ: $(x - 1)(x^2 - x + 3)$.
Материалы школы Юайти