Лицей №2 «Вторая школа» из 7 в 8 класс 2018 год

На каждую задачу даётся 3 попытки. Необходимо обосновать свой ответ. Если вы решили задачу – сразу поднимите руку. Чем больше решено задач, тем лучше!

Для зачёта в 6–7 классах достаточно решить 5 задач, в 8–10 классах – 7 задач.

1. Стулья. Сколькими способами можно расставить в ряд 15 чёрных и 15 красных одинаковых стульев, чтобы никакие два чёрных не стояли рядом?
2. Холмс. К Холмсу пришли 7 человек: 4 рыцаря и 3 лжеца. Он задавал им вопросы «Скажи, X – рыцарь или лжец?» и узнал про каждого, кто он. Объясните, как Холмс сделал это за 6 вопросов.
   
   
3. Вычерк. Найдите все натуральные числа, которые оканчиваются на 97 и после вычеркивания этих двух цифр уменьшаются в целое число раз.
   
   
4. Треугольник. Какое наименьшее число точек нужно отметить на плоскости так, чтобы после стирания любой из них среди оставшихся нашлись три, образующие вершины равностороннего треугольника?
   
   
5. Пятёрки. За контрольную работу 25 школьников получили оценки «3», «4» или «5». На сколько больше было пятёрок, чем троек, если сумма всех оценок равна 106?
   
   
6. Башня. На площадке \(3\times5\) клеток надо поставить кубики так, чтобы получить вид спереди и вид сбоку, как указано:
   
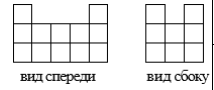
   а) Укажите минимальное число кубиков;
   б) Докажите, что меньшим числом не обойтись.
   
   
7. Сумма. Можно ли выбрать \(N\) натуральных чисел, меньших 100, так чтобы никакие два из них не давали в сумме 100, если \(N=51\)?
   
   
8. Бег. Колонна атлетов длиной 1 км бежит со скоростью 15 км/ч, навстречу им идёт тренер со скоростью 5 км/ч. Добежав до него, атлет разворачивается и бежит назад — с той же скоростью 15 км/ч. Какова будет длина колонны, когда все развернутся?
   
   
9. Точки. На прямой отмечено 9 красных и 9 синих точек в случайном порядке. Можно ли стереть по 4 точки каждого цвета так, чтобы оставшиеся 5 точек каждого цвета шли подряд?
   
   
10. Группы. Существуют ли 20 различных натуральных чисел, что после удаления любого из них остальные можно разбить на 2 группы с равными суммами?

Решения задач

1. Стулья. Пусть 15 красных стульев расставлены. Останется 16 промежутков (между ними и по краям). Для размещения 15 чёрных стульев без соседства выбираем 15 из 16 мест: $C_{16}^{15} = 16$ способов.
   Ответ: 16.
   
   
2. Холмс. Для каждого человека спрашиваем у соседа справа. Если ответ «рыцарь», человек – лжец (и наоборот). Через 6 ответов определит всех, кроме первого. Последний определяется логически, т.к. известно количество рыцарей.
   Ответ: Применение цепочки взаимопроверок.
   
   
3. Вычерк. Число имеет вид $100k + 97$. После вычёркивания получим $k$. По условию $100k + 97 = nk$. Тогда $97 = k(n - 100)$. Возможные $k = 1$ или $k = 97$. Числа: 197 (197:1=197), 9797 (9797:97=101).
   Ответ: 197, 9797.
   
   
4. Треугольник. Достаточно 7 точек – две равносторонние треугольные решётки с общим центром. После удаления любой точки хотя бы три оставшихся образуют правильный треугольник.
   Ответ: 7.
   
   
5. Пятёрки. Пусть $x$ - тройки, $z$ - пятёрки. Из уравнений: $z - x = 6$.
   Ответ: На 6.
   
   
6. Башня. а) Сумма максимальных высот по каждому из видых столбцов спереди и сбоку: минимально 9 кубиков. б) Меньше нельзя, так как каждая строка и столбец требуют минимум столько единиц.
   Ответ: а) 9.
   
   
7. Сумма. Невозможно: максимальное число непопарных пар – 50 (числа 50-99). При $N=51$ две числа гарантированно дополнят до 100.
   Ответ: Нет.
   
   
8. Бег. Все атлеты развернутся одновременно через $\frac{1}{20}$ ч. Колонна восстановится в исходной длине (1 км).
   Ответ: 1 км.
   
   
9. Точки. Да. В каждой группе из 9 точек есть 5 подряд идущих после удаления избыточных.
   Ответ: Да.
   
   
10. Группы. Невозможно: при чётных суммах требуется удаление элемента сохранения чётности суммы остатка, что для 20 чисел не обеспечивается.
    Ответ: Нет.