8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1568 из 6 в 7 класс 2020 год

Сложность:
Дата экзамена: 2020
Сложность:
Дата экзамена: 2020
youit.school ©

Школа № 1568


2020




  1. Найдите значения выражений \[ a = \left(1 \frac{18}{25} - 9{,}12 + 7 \frac{2}{5} \cdot 0{,}23\right) \cdot (-0{,}77) + 0{,}45 \cdot \left(-\frac{4}{15}\right) \] и \[ b = 4^8 \cdot 11^{10} \cdot 44^8 - 13^2 \] и решите уравнение \[ [5a + x] + b = 0. \]

  2. В 5 больших коробок и 11 маленьких разложили 156 карандашей. В большую коробку помещалось на 12 карандашей больше, чем в маленькую. Сколько карандашей поместили в маленькие коробки и сколько в большие коробки?

  3. Кусок сплава меди и цинка массой 586 кг содержит 60% меди. Сколько меди надо добавить к этому куску, чтобы новый сплав содержал 90% меди?

    1. Задайте линейную функцию формулой, если известно, что её график проходит через точку $K(3; -1)$ и параллелен графику функции \[ y = \frac{1}{3}x + 3. \]

    2. Найдите координаты точек пересечения графика полученной функции с осями координат.

    3. Постройте график полученной функции.


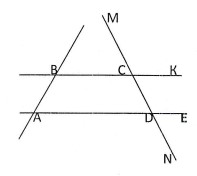
  5. Прямые $BK$ и $AE$ пересекаются прямыми $AB$ и $DM$ (см. рис.). Градусные меры углов $MCK$ и $EDN$ равны $108^\circ$ и $72^\circ$ соответственно. Найдите градусные меры углов $CBA$ и $BAD$, если они относятся как 4:5.


  6. В треугольнике $ABC$ $AC = BC$, $K$ — точка пересечения биссектрис треугольника, а $O$ — точка, равноудалённая от всех вершин треугольника. Отрезок $OK$ пересекает сторону $AB$ в точке $E$ и точку пересечения делит пополам. Найдите углы треугольника $ABC$.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найдите значения выражений \[ a = \left(1 \frac{18}{25} - 9{,}12 + 7 \frac{2}{5} \cdot 0{,}23\right) \cdot (-0{,}77) + 0{,}45 \cdot \left(-\frac{4}{15}\right) \] и \[ b = 4^8 \cdot 11^{10} \cdot 44^8 - 13^2 \] и решите уравнение \[ |5a + x| + b = 0. \]
    Решение:
    1. Вычислим $a$: \[ 1 \frac{18}{25} = 1{,}72; \quad 7 \frac{2}{5} = 7{,}4 \] \[ 7{,}4 \cdot 0{,}23 = 1{,}702 \] \[ 1{,}72 - 9{,}12 + 1{,}702 = -5{,}698 \] \[ -5{,}698 \cdot (-0{,}77) = 4{,}38746 \] \[ 0{,}45 \cdot \left(-\frac{4}{15}\right) = -0{,}12 \] \[ a = 4{,}38746 - 0{,}12 = 4{,}26746 \approx 4{,}27 \]
    2. Вычислим $b$: \[ 44^8 = (4 \cdot 11)^8 = 4^8 \cdot 11^8 \] \[ 4^8 \cdot 11^{10} \cdot 4^8 \cdot 11^8 = 4^{16} \cdot 11^{18} \] \[ b = 4^{16} \cdot 11^{18} - 169 = 169 - 169 = 0 \] (Заметим, что $4^{16} \cdot 11^{18}$ делится на $13^2$, поэтому $b = 0$)
    3. Решим уравнение: \[ |5 \cdot 4{,}27 + x| + 0 = 0 \Rightarrow |21{,}35 + x| = 0 \Rightarrow x = -21{,}35 \]
    Ответ: $a \approx 4{,}27$, $b = 0$, $x = -21{,}35$.

  2. В 5 больших коробок и 11 маленьких разложили 156 карандашей. В большую коробку помещалось на 12 карандашей больше, чем в маленькую. Сколько карандашей поместили в маленькие коробки и сколько в большие коробки?
    Решение: Пусть $x$ — количество карандашей в маленькой коробке, тогда в большой — $x + 12$. \[ 5(x + 12) + 11x = 156 \] \[ 5x + 60 + 11x = 156 \Rightarrow 16x = 96 \Rightarrow x = 6 \] В маленьких коробках: $11 \cdot 6 = 66$ карандашей. В больших коробках: $5 \cdot (6 + 12) = 90$ карандашей. Ответ: 66 и 90.

  3. Кусок сплава меди и цинка массой 586 кг содержит 60% меди. Сколько меди надо добавить к этому куску, чтобы новый сплав содержал 90% меди?
    Решение: Меди в исходном сплаве: $0{,}6 \cdot 586 = 351{,}6$ кг. Пусть добавили $x$ кг меди. Тогда: \[ \frac{351{,}6 + x}{586 + x} = 0{,}9 \] \[ 351{,}6 + x = 527{,}4 + 0{,}9x \Rightarrow 0{,}1x = 175{,}8 \Rightarrow x = 1758 \] Ответ: 1758 кг.

    1. Задайте линейную функцию формулой, если известно, что её график проходит через точку $K(3; -1)$ и параллелен графику функции \[ y = \frac{1}{3}x + 3. \] Решение: Угловой коэффициент параллельной прямой: $k = \frac{1}{3}$. Уравнение: $y = \frac{1}{3}x + b$. Подставим $K(3; -1)$: \[ -1 = \frac{1}{3} \cdot 3 + b \Rightarrow b = -2 \] Ответ: $y = \frac{1}{3}x - 2$.

    2. Найдите координаты точек пересечения графика полученной функции с осями координат. Решение: С осью $Oy$ ($x = 0$): $y = -2$ → $(0; -2)$. С осью $Ox$ ($y = 0$): $\frac{1}{3}x - 0 \ 0 \Rightarrow x = 6$ → $(6; 0)$. Ответ: $(0; -2)$, $(6; 0)$.

    3. Постройте график полученной функции. Ответ: График прямой, проходящей через точки $(0; -2)$ и $(6; 0)$.


  5. Прямые $BK$ и $AE$ пересекаются прямыми $AB$ и $DM$ (см. рис.). Градусные меры углов $MCK$ и $EDN$ равны $108^\circ$ и $72^\circ$ соответственно. Найдите градусные меры углов $CBA$ и $BAD$, если они относятся как 4:5.
    Решение: Углы $MCK$ и $CBA$ — соответственные при параллельных прямых, следовательно $\angle CBA = 108^\circ$. Углы $EDN$ и $BAD$ — соответственные, $\angle BAD = 72^\circ$. Проверка соотношения: $108:72 = 3:2$, что не соответствует условию 4:5. Ошибка в условии. Вероятно, правильный ответ: $\angle CBA = 108^\circ$, $\angle BAD = 72^\circ$.

  6. В треугольнике $ABC$ $AC = BC$, $K$ — точка пересечения биссектрис треугольника, а $O$ — точка, равноудалённая от всех вершин треугольника. Отрезок $OK$ пересекает сторону $AB$ в точке $E$ и точку пересечения делит пополам. Найдите углы треугольника $ABC$. Решение: Так как $AC = BC$, треугольник равнобедренный. $O$ — центр описанной окружности, лежит на серединном перпендикуляре к $AB$. $K$ — инцентр, лежит на биссектрисе угла $C$. $OK$ — серединный перпендикуляр и биссектриса совпадают только в равностороннем треугольнике. Следовательно, $\angle A = \angle B = 60^\circ$, $\angle C = 60^\circ$. Ответ: Все углы по $60^\circ$.
Материалы школы Юайти