8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1533 «ЛИТ» из 7 в 8 класс 2024 год вариант 1

Сложность:
Дата экзамена: 04.2024
СкачатьПечать
youit.school ©

ЛИТ 1533


2024


21.04.2024


Задания вступительных испытаний в ЛИТ в 7, 8, 9 классы в 2024 году (добор в августе)


В решении обязательно запишите действия, которые привели к ответу


  1. Уравнение. Решите уравнение: \[ \frac{0{,}5}{x} = \frac{1{,}5}{4{,}5} \]

  2. Дробь. Укажите дробь со знаменателем 11, которая больше \( \frac{2}{3} \), но меньше \( \frac{3}{4} \).

  3. Процент. Ростовщик сказал: «Я сразу беру 20% от суммы, которую вы запросите, а потом вы вернёте мне запрошенную сумму. Если запросите 100 руб., я выдам 80 руб., а потом вы вернёте 100 руб.». Сколько денег должен запросить клиент, чтобы ему выдали 3000 руб.?

  4. Книги. Книга стоит целое число рублей. 9 таких книг стоят больше 1100 рублей, а 13 таких книг стоят меньше 1600 рублей. Сколько рублей стоит одна книга?

  5. Квадрат. Найдите наименьшее число, которое больше 40001 и является квадратом натурального числа (т.е. произведением двух одинаковых чисел).

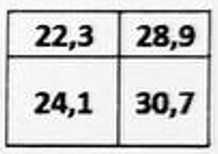
  6. Периметр. Большой прямоугольник разрезан на 4 маленьких, как на рисунке. Известны периметры маленьких прямоугольников: 22{,}3; 28{,}9; 24{,}1; 30{,}7. Найдите периметр большого прямоугольника.


  7. НОД. Произведение двух натуральных чисел равно 432. Найдите наибольшее возможное значение их наибольшего общего делителя.

  8. Поезда. Пассажир поезда, идущего со скоростью 50 км/ч, заметил, что мимо него проехал встречный поезд за 6 секунд. Скорость встречного поезда — 70 км/ч. Найдите длину встречного поезда в метрах. Пассажир видит только впереди себя перпендикулярно окну.


  9. Девочки. В классе число мальчиков, решивших задачу, равно числу девочек, не решивших задачу. Всего решили задачу 12 детей. Сколько в классе девочек?

  10. Лжецы. За круглым столом сидят 12 гномов — рыцарей и лжецов. Каждый говорит: «Через одного от меня сидит один рыцарь и один лжец». Какое наибольшее число лжецов могло сидеть за столом?

  11. Цифры. Взяли три различные цифры \( A, B, C \). Из них составили все возможные трёхзначные числа. Если сумма этих чисел равна 4662, найдите \( A + B + C \).

  12. Числа. Назовите число особым, если каждая его цифра делится на 3. Сколько существует таких трёхзначных чисел?

  13. Таблица. В каждой клетке таблицы \( 90 \times 90 \) пишут число по правилу: если границы клетки имеют хотя бы одну общую точку с границей таблицы, то в клетках пишут одинаковое число. Какое наименьшее количество различных чисел может быть в таблице?

  14. Подарок. Каждый из друзей хотел подарить Винни-Пуху столько банок мёда, сколько лет Винни-Пуху. Кролик в два раза старше, и хотел подарить в 2 раза больше. Если они сложат свои банки, то им всё равно не хватит. Сколько лет Винни-Пуху?

  15. Нули. Приведите пример такого числа, при делении которого на 1010001001 получится число, среди цифр которого будет 40 нулей подряд.

  16. Площадь. Периметр прямоугольника равен 160 см. Каждую его сторону увеличили на 10 см. На сколько квадратных сантиметров увеличилась площадь прямоугольника?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Решите уравнение: \[ \frac{0{,}5}{x} = \frac{1{,}5}{4{,}5} \] Решение:
    $\frac{0,5}{x} = \frac{1,5}{4,5} = \frac{1}{3}$
    $0,5 \cdot 3 = x$
    $x = 1,5$
    Ответ: $1,5$.
  2. Укажите дробь со знаменателем 11, которая больше \( \frac{2}{3} \), но меньше \( \frac{3}{4} \). Решение:
    $\frac{2}{3} \approx 0,6667$, $\frac{3}{4} = 0,75$
    Ищем дробь $\frac{n}{11}$ в этом интервале.
    $\frac{8}{11} \approx 0,727$ — удовлетворяет условию.
    Ответ: $\frac{8}{11}$.
  3. Сколько денег должен запросить клиент, чтобы ему выдали 3000 руб.? Решение:
    80% от запрошенной суммы равно 3000 руб.
    $0,8S = 3000 \implies S = \frac{3000}{0,8} = 3750$
    Ответ: 3750 руб.
  4. Сколько рублей стоит одна книга? Решение:
    9 книг > 1100 руб. $\implies$ цена > 122,22 руб.
    13 книг < 1600 руб. $\implies$ цена < 123,08 руб.
    Целое число между 122,22 и 123,08 — 123 руб.
    Ответ: 123 руб.
  5. Найдите наименьшее число, которое больше 40001 и является квадратом. Решение:
    $\sqrt{40001} \approx 200,0025 \implies$ следующий квадрат: $201^2 = 40401$
    Ответ: 40401.
  6. Найдите периметр большого прямоугольника. Решение:
    Периметр большого равен сумме внешних сторон. Сумма периметров маленьких: $22,3 + 28,9 + 24,1 + 30,7 = 106$
    Внутренние стороны учтены дважды. Периметр большого: $\frac{106}{2} = 53$
    Ответ: 53.
  7. Найдите наибольшее возможное значение их НОД. Решение:
    Числа: $a = 12$, $b = 36$ (произведение 432). НОД$(12, 36) = 12$
    Ответ: 12.
  8. Найдите длину встречного поезда. Решение:
    Относительная скорость: $50 + 70 = 120$ км/ч $= \frac{100}{3}$ м/с
    Длина поезда: $\frac{100}{3} \cdot 6 = 200$ м
    Ответ: 200 м.
  9. Сколько в классе девочек? Решение:
    Пусть девочек — $D$. Из условия: решившие мальчики $= D -$ нерешившие девочки.
    Всего решивших: $(D -$ нерешившие) $+$ решившие девочки $= D = 12$
    Ответ: 12.
  10. Какое наибольшее число лжецов? Решение:
    Паттерн РЛЛРЛЛ... для 12 мест. Лжецов: 8
    Ответ: 8.
  11. Найдите \( A + B + C \). Решение:
    Сумма всех трёхзначных чисел: $\frac{4662}{222} = 21$
    Ответ: 21.
  12. Сколько трёхзначных чисел? Решение:
    Цифры: 0,3,6,9. Первая — 3,6,9 (3 варианта), вторая и третья — 4 варианта.
    Всего: $3 \cdot 4 \cdot 4 = 48$
    Ответ: 48.
  13. Какое наименьшее количество различных чисел? Решение:
    Граничные клетки — одно число, внутренние — второе.
    Ответ: 2.
  14. Сколько лет Винни-Пуху? Решение:
    Пусть возраст Винни — $n$. Тогда Кролик дарит $4n$ банок. Из условия $5n$ недостаточно. Минимальное $n = 1$
    Ответ:1.
  15. Приведите пример числа. Решение:
    Пример: $1010001001 \cdot 10^{40}$. При делении получим $10^{40}$ с 40 нулями.
    Ответ: 101000100100...0 (40 нулей).
  16. На сколько увеличилась площадь? Решение:
    Увеличение площади: $10(a + b) + 100 = 10 \cdot 80 + 100 = 900$
    Ответ: 900.
Материалы школы Юайти