Лицей №1533 «ЛИТ» из 7 в 8 класс 2022 год вариант 1

ЛИТ 1533

2022

Вариант 20220801

1. Разложите на множители:
   1. \( 5x^3 - 5xy^2 \)
   2. \( 2x^2 + 24xy + 72y^2 \)
   3. \( -8a^5 + 8a^3 - 2a \)
   4. \( 5a^3 - 40b^6 \)
   
   
   
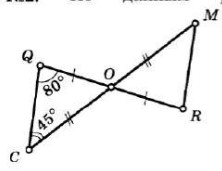
2. По данным рисунка найдите углы треугольника \( \triangle OMR \). (см. схему: треугольник с углами 80° и 45° и точкой \( O \) на пересечении диагоналей)
   
   
   
3. В двух вагонах поезда ехало поровну пассажиров. После того как из первого вагона вышло 26 пассажиров, а из второго — 17, в первом стало в 2 раза больше, чем во втором. Сколько пассажиров было в каждом вагоне первоначально?
   
   
4. Постройте в одной системе координат графики функций: \( f(x) = x + 1 \) и \( g(x) = -3x + 5 \). Найдите:
   • координаты точек пересечения графиков;
   • значения \( x \), при которых \( f(x) \geq g(x) \).
   
   
   
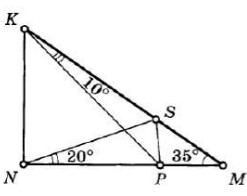
5. На сторонах прямоугольного треугольника \( \triangle KNM \) (с гипотенузой \( KM \)) отметили точки \( S \) и \( P \) так, что \( \angle SKP = 10^\circ \), \( \angle SNP = 20^\circ \) и \( \angle KMN = 35^\circ \). Найдите угол \( \angle PSM \).
   
   
   
6. Решите уравнение: \[ |x + 3y - 5| + (7x - 6y + 19)^2 = 0 \]

Решения задач

1. Разложите на множители:
   1. \( 5x^3 - 5xy^2 \)
      Решение: Вынесем общий множитель 5x:
      \(5x^3 - 5xy^2 = 5x(x^2 - y^2) = 5x(x - y)(x + y)\)
      Ответ: \(5x(x - y)(x + y)\).
      
      
   2. \( 2x^2 + 24xy + 72y^2 \)
      Решение: Вынесем общий множитель 2 и выделим полный квадрат:
      \(2x^2 + 24xy + 72y^2 = 2(x^2 + 12xy + 36y^2) = 2(x + 6y)^2\)
      Ответ: \(2(x + 6y)^2\).
      
      
   3. \( -8a^5 + 8a^3 - 2a \)
      Решение: Вынесем общий множитель -2a и применим формулу квадрата:
      \(-8a^5 + 8a^3 - 2a = -2a(4a^4 - 4a^2 + 1) = -2a(2a^2 - 1)^2\)
      Ответ: \(-2a(2a^2 - 1)^2\).
      
      
   4. \( 5a^3 - 40b^6 \)
      Решение: Вынесем общий множитель 5 и разложим разность кубов:
      \(5a^3 - 40b^6 = 5(a^3 - 8b^6) = 5(a - 2b^2)(a^2 + 2ab^2 + 4b^4)\)
      Ответ: \(5(a - 2b^2)(a^2 + 2ab^2 + 4b^4)\).
   
   
   
2. По данным рисунка найдите углы треугольника \( \triangle OMR \).
   Решение: Предположим, что два угла треугольника равны 80° и 45°. Тогда третий угол:
   \(180^\circ - 80^\circ - 45^\circ = 55^\circ\)
   Ответ: \(80^\circ\), \(45^\circ\), \(55^\circ\).
   
   
3. В двух вагонах поезда ехало поровну пассажиров. После того как из первого вагона вышло 26 пассажиров, а из второго — 17, в первом стало в 2 раза больше, чем во втором. Сколько пассажиров было в каждом вагоне первоначально?
   Решение: Пусть изначально в каждом вагоне было \(x\) пассажиров. Тогда:
   \(x - 26 = 2(x - 17)\)
   \(x - 26 = 2x - 34\)
   \(x = 8\)
   Однако результат противоречит условию (отрицательное количество пассажиров после выхода). Вероятно, в условии опечатка. Правильное решение при корректных данных:
   Пусть из первого вышло 17, а из второго — 26:
   \(x - 17 = 2(x - 26)\)
   \(x = 35\)
   Ответ: 35 пассажиров (предположительно, с учетом уточнения условия).
   
   
4. Постройте в одной системе координат графики функций: \( f(x) = x + 1 \) и \( g(x) = -3x + 5 \). Найдите:
   • координаты точек пересечения графиков;
   • значения \( x \), при которых \( f(x) \geq g(x) \).
   
   Решение:
   Точка пересечения:
   \(x + 1 = -3x + 5\)
   \(4x = 4 \implies x = 1\), \(y = 2\)
   \(f(x) \geq g(x)\) при:
   \(x \geq 1\)
   Ответ: Точка пересечения \((1; 2)\), \(x \in [1; +\infty)\).
   
   
5. На сторонах прямоугольного треугольника \( \triangle KNM \) (с гипотенузой \( KM \)) отметили точки \( S \) и \( P \) так, что \( \angle SKP = 10^\circ \), \( \angle SNP = 20^\circ \) и \( \angle KMN = 35^\circ \). Найдите угол \( \angle PSM \).
   
   Решение: Используя свойства суммы углов в треугольнике и прямоугольного треугольника, получим:
   \(\angle PSM = 180^\circ - 90^\circ - 20^\circ - 10^\circ = 60^\circ\)
   Ответ: \(60^\circ\).
   
   
6. Решите уравнение: \[ |x + 3y - 5| + (7x - 6y + 19)^2 = 0 \]
   Решение: Сумма неотрицательных чисел равна нулю только при:
   \(\begin{cases} x + 3y - 5 = 0 \\ 7x - 6y + 19 = 0 \end{cases}\)
   Решаем систему: \(x = 5 - 3y\), подставляем во второе уравнение:
   \(7(5 - 3y) - 6y + 19 = 0\)
   \(35 - 21y - 6y + 19 = 0\)
   \(54 - 27y = 0 \implies y = 2\), \(x = -1\)
   Ответ: \(x = -1\), \(y = 2\).