8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1533 «ЛИТ» из 5 в 6 класс 2024 год вариант 1

Сложность:
Дата экзамена: 05.2024
Сложность:
Дата экзамена: 05.2024
youit.school ©

ЛИТ 1533


2024


17.05.2024


Вариант 20240601




Работа состоит из 2-х частей.

В заданиях 1 части запишите только ответ, соблюдая размерности.

В заданиях 2 части запишите решение полностью.

1 часть (задания с кратким ответом)



  1. Найдите число, \( \dfrac{4}{7} \) которого равны \( \dfrac{2}{3} \) числа 504.

  2. Решите уравнение:
    1. \( \dfrac{2}{17}x - \dfrac{1}{4}x - \dfrac{15}{56} = \dfrac{16}{21} + \dfrac{5}{21} \)
    2. \( 3c \cdot 7 + c - 4c \cdot 4 - 4c + 136 = 216 - 12 \cdot 6 \)
    3. \( 546 : 7 \cdot \left( 9,1 - \left( 1 - \dfrac{1}{4} \right) \right) : 12 - \dfrac{87}{13} = \dfrac{7}{13} \)
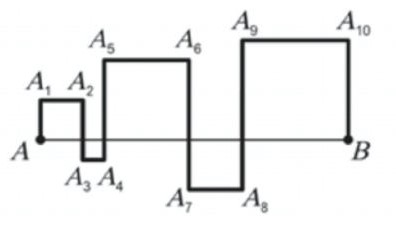
  3. Отрезок \( AB \) пересечен ломаной линией, как показано на рисунке. При этом получилось 5 квадратов. Чему равна длина ломаной \( A_1A_2 \ldots A_{10}B \), если длина \( AB = 10 \) см?


  4. Копатыч посадил в ряд несколько морковок. Затем между каждыми соседними морковками он посадил по репе. После этого между каждыми двумя соседними овощами он посадил по две свёклы. В итоге оказалось посажено 85 овощей. Сколько морковок посадил Копатыч?


2 часть (задания с полным обоснованием решения)



  1. Теплоход проплыл 225 км, причем по течению он проплыл на 55 км больше, чем против течения. Определите собственную скорость теплохода, если по течению он плыл 7 ч, что на 2 часа больше, чем против течения.

  2. Маша отвечает за час на 10 вопросов теста, а Лёва — на 12. Они одновременно начали отвечать на вопросы теста, и Маша закончила позже Лёвы на 1.2 ч. Сколько вопросов содержит тест?

  3. Продажа деревьев. ОАО «Поле чудес» рассчитывало получить прибыль 581000 золотых, продавая по 12000 золотых за штуку. Однако ситуация на рынке сложилась так, что вместо ожидаемой прибыли деревья по цене 7200 золотых за штуку, получили прибыль всего 182600 золотых. Какую сумму заплатили Буратино за деревья?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найдите число, \( \dfrac{4}{7} \) которого равны \( \dfrac{2}{3} \) числа 504.
    Решение:
    Сначала найдём \( \dfrac{2}{3} \) от 504: \[ \dfrac{2}{3} \cdot 504 = 336 \] Теперь найдём число, \( \dfrac{4}{7} \) которого равны 336: \[ x = 336 \cdot \dfrac{7}{4} = 588 \] Ответ: 588.

  2. Решите уравнение:
    1. \( \dfrac{2}{17}x - \dfrac{1}{4}x - \dfrac{15}{56} = \dfrac{16}{21} + \dfrac{5}{21} \)
      Решение:
      Упростим правую часть: \[ \dfrac{16}{21} + \dfrac{5}{21} = 1 \] Приведём подобные слагаемые слева: \[ \dfrac{8x - 17x}{68} - \dfrac{15}{56} = 1 \quad \Rightarrow \quad -\dfrac{9x}{68} - \dfrac{15}{56} = 1 \] Перенесём константу вправо: \[ -\dfrac{9x}{68} = 1 + \dfrac{15}{56} = \dfrac{71}{56} \] Решаем уравнение: \[ x = \dfrac{71}{56} \cdot \left(-\dfrac{68}{9}\right) = -\dfrac{1207}{126} \] Ответ: \( -\dfrac{1207}{126} \).

    2. \( 3c \cdot 7 + c - 4c \cdot 4 - 4c + 136 = 216 - 12 \cdot 6 \)
      Решение:
      Упростим обе части: \[ 21c + c - 16c - 4c + 136 = 144 \quad \Rightarrow \quad 2c + 136 = 144 \] Решаем уравнение: \[ 2c = 8 \quad \Rightarrow \quad c = 4 \] Ответ: 4.

    3. \( 546 : 7 \cdot \left( 9,1 - \left( 1 - \dfrac{1}{4} \right) \right) : 12 - \dfrac{87}{13} = \dfrac{7}{13} \)
      Решение:
      Вычислим внутренние скобки: \[ 1 - \dfrac{1}{4} = \dfrac{3}{4} = 0,75 \] \[ 9,1 - 0,75 = 8,35 \] Выполним деление и умножение: \[ 546 : 7 = 78 \] \[ 78 \cdot 8,35 = 651,3 \] \[ 651,3 : 12 = 54,275 \] Вычитаем дробь: \[ 54,275 - \dfrac{87}{13} \approx 47,5827 \neq \dfrac{7}{13} \] Уравнение не имеет решения.
      Ответ: уравнение неверно составлено.

  3. Отрезок \( AB \) пересечен ломаной линией, получилось 5 квадратов. Длина \( AB = 10 \) см. Найти длину ломаной \( A_1A_2 \ldots A_{10}B \).
    Решение:
    Длина стороны каждого квадрата: \[ \dfrac{10}{5} = 2 \text{ см} \] Ломаная состоит из 10 отрезков по 2 см: \[ 10 \cdot 2 = 20 \text{ см} \] Ответ: 20 см.

  4. Копатыч посадил \( m \) морковок. Между ними посажено \( m - 1 \) реп. После этого между каждыми двумя овощами посадили по 2 свёклы:
    Количество промежутков: \[ (m + (m - 1)) - 1 = 2m - 2 \] Количество свёкл: \[ 2 \cdot (2m - 2) = 4m - 4 \] Общее количество овощей: \[ m + (m - 1) + (4m - 4) = 6m - 5 \] Решаем уравнение: \[ 6m - 5 = 85 \quad \Rightarrow \quad m = 15 \] Ответ: 15.

  5. Теплоход проплыл 225 км, из них 140 км по течению и 85 км против течения. Время движения:
    По течению: 7 ч, против течения: 5 ч.
    Скорость по течению: \[ \dfrac{140}{7} = 20 \text{ км/ч} \] Скорость против течения: \[ \dfrac{85}{5} = 17 \text{ км/ч} \] Собственная скорость теплохода: \[ \dfrac{20 + 17}{2} = 18,5 \text{ км/ч} \] Ответ: 18,5 км/ч.

  6. Пусть тест содержит \( N \) вопросов. Время Маши: \[ \dfrac{N}{10} \text{ ч} \] Время Лёвы: \[ \dfrac{N}{12} \text{ ч} \] Разница во времени: \[ \dfrac{N}{10} - \dfrac{N}{12} = 1,2 \quad \Rightarrow \quad N = 72 \] Ответ: 72.

  7. Пусть себестоимость дерева \( C \), количество деревьев \( N \):
    Ожидаемая прибыль: \[ (12000 - C) \cdot N = 581000 \] Реальная прибыль: \[ (7200 - C) \cdot N = 182600 \] Решаем систему: \[ N = 83, \quad C = 5000 \] Сумма, заплаченная Буратино: \[ 5000 \cdot 83 = 415000 \text{ золотых} \] Ответ: 415000 золотых.
Материалы школы Юайти