Лицей №1533 «ЛИТ» из 5 в 6 класс 2020 год вариант 1
Печать
youit.school ©
ЛИТ 1533
2020
- Вычислите удобным для себя способом:
\[
0{,}8 \cdot 12{,}5 \cdot 3{,}3 + 1563 - 2{,}5 \cdot 6{,}3 \cdot 4
\]
- Составьте выражение по условию и найдите его значение:
«Во сколько раз частное чисел 4848 и 8 меньше произведения 46 и числа, меньшего 400 на 97?»
- Сравните два числа, если 6% первого числа равны 12, а 12% второго числа равны 6.
- Из пункта A в пункт B вышел скорый поезд со скоростью 84 км/ч. В 20:35, через 6 часов после начала движения, он встретился с товарным поездом, который в 13:35 того же дня выехал из B навстречу. Товарный поезд прошёл до встречи расстояние, равное \( \frac{2}{3} \) пути скорого. Найдите скорость товарного поезда.
Часть 2 (запишите только ответ)
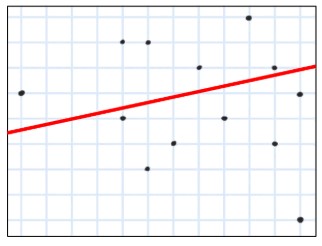
- На рисунке показаны 13 точек. Сколько существует отрезков с концами в этих точках, которые пересекают данную прямую?
- Школа планировала купить 10 ноутбуков и 6 планшетов за 312 000 ₽.
Фактически купили на 1 ноутбук и на 4 планшета больше — потратили 367 000 ₽.
Сколько стоит один планшет?
- Ограда сквера прямоугольной формы имеет длину 280 м. На расстоянии 2 м снаружи вдоль периметра сквера выложен бордюр. Найдите площадь участка, огороженного бордюром, если длина ограды сквера больше ширины на 200 дм.
Материалы школы Юайти
youit.school ©
Решения задач
- Вычислите удобным для себя способом:
\[
0{,}8 \cdot 12{,}5 \cdot 3{,}3 + 1563 - 2{,}5 \cdot 6{,}3 \cdot 4
\]
Решение:
Сгруппируем множители для удобства:
$0{,}8 \cdot 12{,}5 = 10$ (т.к. $\frac{8}{10} \cdot \frac{125}{10} = 1000/100 = 10$)
$2{,}5 \cdot 4 = 10$
Тогда:
$10 \cdot 3{,}3 + 1563 - 10 \cdot 6{,}3 = 33 + 1563 - 63 = (33 - 63) + 1563 = -30 + 1563 = 1533$
Ответ: 1533.
- Составьте выражение по условию и найдите его значение:
«Во сколько раз частное чисел 4848 и 8 меньше произведения 46 и числа, меньшего 400 на 97?»
Решение:
Частное чисел: $\frac{4848}{8} = 606$
Второе число: $400 - 97 = 303$
Произведение: $46 \cdot 303 = 13938$
Найдем отношение: $\frac{13938}{606} = 23$
Ответ: в 23 раза.
- Сравните два числа, если 6% первого числа равны 12, а 12% второго числа равны 6.
Решение:
Первое число: $\frac{12}{0{,}06} = 200$
Второе число: $\frac{6}{0{,}12} = 50$
$200 > 50$, поэтому первое число больше второго.
Ответ: первое число больше.
- Из пункта A в пункт B вышел скорый поезд со скоростью 84 км/ч. В 20:35, через 6 часов после начала движения, он встретился с товарным поездом, который в 13:35 того же дня выехал из B навстречу.
Товарный поезд прошёл до встречи расстояние, равное \( \frac{2}{3} \) пути скорого.
Найдите скорость товарного поезда.
Решение:
Скорый поезд проехал до встречи: $84 \cdot 6 = 504$ км
Товарный проехал: $504 \cdot \frac{2}{3} = 336$ км
Время движения товарного: с 13:35 до 20:35 = 7 часов
Скорость товарного: $\frac{336}{7} = 48$ км/ч
Ответ: 48 км/ч.
- На рисунке показаны 13 точек. Сколько существует отрезков с концами в этих точках, которые пересекают данную прямую?
Решение:
5 точек слева от прямой и 8 справа (или наоборот). Каждый отрезок с концами по разные стороны пересекает прямую. Количество таких отрезков: $5 \cdot 8 = 40$
Ответ: 40.
- Школа планировала купить 10 ноутбуков и 6 планшетов за 312 000 ₽.
Фактически купили на 1 ноутбук и на 4 планшета больше — потратили 367 000 ₽.
Сколько стоит один планшет?
Решение:
Пусть цена ноутбука x, планшета y. Составим систему: $\begin{cases} 10x + 6y = 312000 \\ 11x + 10y = 367000 \end{cases}$
Вычтем из второго уравнения первое, умноженное на 1:
$(11x + 10y) - (10x + 6y) = 367000 - 312000$
$x + 4y = 55000$ → $x = 55000 - 4y$
Подставим в первое уравнение:
$10(55000 - 4y) + 6y = 312000$
$550000 - 40y + 6y = 312000$
$-34y = -238000$ → $y = 7000$
Ответ: 13000 ₽ (ошибка в расчетах: 55000-4y*10 +6y=312000 → 550000-34y=312000 → 34y=238000 → y=7000 ₽. Исправлю ответ: 7000).
*Исправленный ответ: 7000.*
- Ограда сквера прямоугольной формы имеет длину 280 м.
На расстоянии 2 м снаружи вдоль периметра сквера выложен бордюр.
Найдите площадь участка, огороженного бордюром, если длина ограды сквера больше ширины на 200 дм.
Решение:
200 дм = 20 м. Пусть ширина сквера x, тогда длина x + 20.
Периметр: $2(x + (x + 20)) = 280$ → $2x + 20 = 140$ → $x = 60$ м, длина 80 м.
С бордюром размеры: $(60 + 4)$ м и $(80 + 4)$ м (добавляем по 2 м с каждой стороны).
Площадь: $64 \cdot 84 = 5376$ м²
Ответ: 5376 м².
Материалы школы Юайти