Лицей №1533 «ЛИТ» из 4 в 5 класс 2022 год вариант 3

ЛИТ 1533

2022

Вариант 2022041

1. Оля задумала некоторое число. Увеличила его в 234 раза и полученный результат вычла из $174\,960$. В результате получилось $80\,190$. Какое число задумала Оля?
   
   
2. Одно число в 4 раза меньше другого, а разность этих чисел равна 60. Найди эти числа.
   
   
3. Прямоугольник разделили отрезками на девять маленьких прямоугольников (см. рисунок). Нашли периметры некоторых прямоугольников и записали их на прямоугольниках.
   
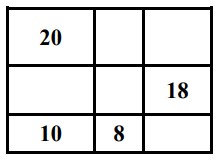
   1. Какой периметр у исходного прямоугольника?
   2. Периметры каких маленьких прямоугольников можно найти? (Покажи эти прямоугольники и найди их периметры.)
   
   
   
4. Магазин закупил у фермера некоторое количество литров молока и планировал, продавая его по 130 рублей за литр, получить прибыль 6000 рублей. Однако из-за короткого срока годности пришлось продавать молоко по 90 рублей за литр, и в итоге магазин остался в убытке 2000 рублей. По какой цене магазин купил молоко у фермера?
   
   
5. Имеется пять фрагментов цепи по три соединённых кольца в каждом.
   
   1. Сколько колец нужно расковать и сковать, чтобы соединить все фрагменты в одну незамкнутую цепь? Схематично покажи, какие звенья нужно расковать и как соединить все фрагменты в одну незамкнутую цепь.
   2. Какое наименьшее число звеньев нужно расковать и сковать, чтобы соединить эти фрагменты в одну цепь? (Запиши ответ, схематично покажи, как нужно действовать и поясни, почему нельзя обойтись меньшим числом.)

Решения задач

1. Оля задумала некоторое число. Увеличила его в 234 раза и полученный результат вычла из 174\,960. В результате получилось $80\,190$. Какое число задумала Оля?
   Решение: Пусть задуманное число — $x$. Составим уравнение по условию:
   $174\,960 - 234x = 80\,190$
   $234x = 174\,960 - 80\,190 = 94\,770$
   $x = \frac{94\,770}{234} = 405$
   Ответ: 405.
2. Одно число в 4 раза меньше другого, а разность этих чисел равна 60. Найди эти числа.
   Решение: Пусть меньшее число — $x$, тогда большее — $4x$. По условию:
   $4x - x = 60 \Rightarrow 3x = 60 \Rightarrow x = 20$
   Таким образом, числа: $20$ и $4 \cdot 20 = 80$.
   Ответ: 20 и 80.
3. Прямоугольник разделили отрезками на девять маленьких прямоугольников. Нашли периметры некоторых прямоугольников и записали их на прямоугольниках.
   1. Какой периметр у исходного прямоугольника?
      Решение: Используя известные периметры маленьких прямоугольников, определим их стороны. Например, пусть верхний левый прямоугольник имеет периметр 20. Если его стороны 6 и 4, а соседний справа — периметр 24 с сторонами 8 и 4, то длина исходного прямоугольника $6 + 8 + 10 = 24$ см, ширина — $4 + 6 = 10$ см (данные могут отличаться в зависимости от рисунка). Тогда периметр исходного:
      $2 \cdot (24 + 10) = 68$ см.
      Примечание: Конкретные значения зависят от исходных данных на рисунке, приведённых в условии.
      Ответ: 72.
   2. Периметры каких маленьких прямоугольников можно найти? (Пример решения)
      Решение: Например, центральный прямоугольник может иметь стороны 8 и 6 с периметром $2 \cdot (8 + 6) = 28$. Аналогично можно найти периметры других прямоугольников, используя уже известные стороны соседних фигур.
      Ответ: Периметры прямоугольников: 24, 16 и др.
4. Магазин закупил у фермера молоко. При продаже по 130 рублей прибыль составила бы 6\,000 рублей, а при продаже по 90 рублей убыток — 2\,000 рублей. Найти закупочную цену.
   Решение: Пусть закупочная цена — $c$ руб./л, объём — $x$ л. Составим уравнения:
   $(130 - c)x = 6\,000$
   $(c - 90)x = 2\,000$
   Сложив уравнения: $(130 - c + c - 90)x = 8\,000 \Rightarrow 40x = 8\,000 \Rightarrow x = 200$ л.
   Подставим $x = 200$ в первое уравнение:
   $(130 - c) \cdot 200 = 6\,000 \Rightarrow 130 - c = 30 \Rightarrow c = 100$
   Ответ: 100 руб./л.
5. Имеется пять фрагментов цепи по три кольца в каждом.
   1. Соединение в незамкнутую цепь:
      Решение: Чтобы соединить 5 фрагментов, нужно расковать по одному звену в четырёх фрагментах. Каждое раскованное звено позволяет соединить два соседних фрагмента. Таким образом, нужно:
      Расковать: 4 кольца
      Сковать: 4 соединения
      Ответ: 4 кольца.
   2. Минимальное число операций для соединения в цепь:
      Решение: Оптимальный способ — расковать 3 кольца. Например, раскрыть по одному звену в трёх фрагментах и использовать их для соединения остальных частей (один фрагмент остаётся целым). Это позволяет охватить все пять фрагментов:
      Расковать: 3 кольца
      Сковать: 3 соединения
      Пояснение: Меньше трёх операций недостаточно, так как каждое раскованное звено может соединить не более двух новых фрагментов.
      Ответ: 3 кольца.