Лицей №1533 «ЛИТ» из 4 в 5 класс 2022 год вариант 2

ЛИТ 1533

2022

Вариант 2022041

1. Миша задумал некоторое число. Увеличил его в 423 раза и полученный результат вычел из $313\,443$. В результате получилось $58\,374$. Какое число задумал Миша?
   
   
2. Разность двух чисел равна 249, а частное от деления одного на другое равно 4. Найдите эти числа.
   
   
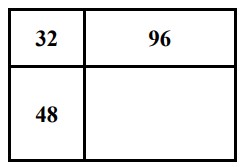
3. Прямоугольник разделили двумя отрезками на четыре прямоугольника. Площади трёх из них равны: 32 см², 96 см² и 48 см². Найдите площадь всего прямоугольника.
   
   
   
4. Стекольщик должен нарезать 120 стекол. За правильно нарезанное стекло он получает 40 руб., а за неправильно нарезанное — с него удерживают 80 руб. Сколько стекол стекольщик нарезал неправильно, если ему за работу заплатили 3600 руб.?
   
   
5. У портного Вени была любимая линейка длиной ровно 9 дм, но вся шкала на ней стёрлась. Линейку можно использовать только чтобы отмерять ровно 9 дм.
   
   
   1. Какие деления нужно восстановить, чтобы можно было одним прикладыванием отмерять целое количество дециметров от 1 до 9? Объясни, как отмерить отрезок 5 дм.
   2. Какое минимальное количество делений потребуется восстановить? Объясни, почему нельзя обойтись меньшим количеством, и покажи, как отмерить все 9 отрезков.

Решения задач

1. Миша задумал некоторое число. Увеличил его в 423 раза и полученный результат вычел из 313\,443. В результате получилось $58\,374$. Какое число задумал Миша?
   Решение:
   Пусть задуманное число — $x$. По условию:
   $313\,443 - 423x = 58\,374$
   $423x = 313\,443 - 58\,374 = 255\,069$
   $x = \frac{255\,069}{423} = 603$
   Проверка: $423 \cdot 603 = 255\,069$
   Ответ: 603.
   
   
2. Разность двух чисел равна 249, а частное от деления одного на другое равно 4. Найдите эти числа.
   Решение:
   Пусть числа — $a$ и $b$, где $a > b$. Тогда:
   $\begin{cases} a - b = 249 \\ \frac{a}{b} = 4 \end{cases}$
   Выразим $a = 4b$ и подставим в первое уравнение:
   $4b - b = 249 \implies 3b = 249 \implies b = 83$
   $a = 4 \cdot 83 = 332$
   Проверка: $332 - 83 = 249$, $332:83 = 4$
   Ответ: 332 и 83.
   
   
3. Прямоугольник разделили двумя отрезками на четыре прямоугольника. Площади трёх из них равны: 32 см², 96 см² и 48 см². Найдите площадь всего прямоугольника.
   Решение:
   Предположим, прямоугольник разделён вертикально и горизонтально. Обозначим вертикальные части $a$ и $b$, горизонтальные $c$ и $d$. Тогда площади:
   - Верхний левый: $a \cdot c = 32$ см² - Верхний правый: $b \cdot c = 96$ см² - Нижний левый: $a \cdot d = 48$ см²
   Из первого и третьего уравнений: $\frac{a \cdot d}{a \cdot c} = \frac{48}{32} \implies \frac{d}{c} = \frac{3}{2} \implies d = 1,5c$ Из первого и второго уравнений: $\frac{b \cdot c}{a \cdot c} = \frac{96}{32} \implies \frac{b}{a} = 3 \implies b = 3a$
   Общая высота: $c + d = c + 1,5c = 2,5c$ Общая ширина: $a + b = a + 3a = 4a$
   Площадь оставшегося прямоугольника: $b \cdot d = 3a \cdot 1,5c = 4,5a \cdot c = 4,5 \cdot 32 = 144$ см² Общая площадь: $32 + 96 + 48 + 144 = 320$ см²
   Ответ: 320 см².
   
   
4. Стекольщик должен нарезать 120 стекол. За правильно нарезанное стекло он получает 40 руб., а за неправильно нарезанное — с него удерживают 80 руб. Сколько стекол стекольщик нарезал неправильно, если ему за работу заплатили 3600 руб.?
   Решение:
   Пусть правильно нарезано $x$ стекол, неправильно — $y$. $\begin{cases} x + y = 120 \\ 40x - 80y = 3600 \end{cases}$ Выразим $x = 120 - y$, подставим во второе уравнение: $40(120 - y) - 80y = 3600$ $4800 - 120y = 3600 \implies 120y = 1200 \implies y = 10$
   Проверка: $110 \cdot 40 - 10 \cdot 80 = 4400 - 800 = 3600$ Ответ: 10 стекол.
   
   
5. У портного Вени была любимая линейка длиной ровно 9 дм, но вся шкала на ней стёрлась. Линейку можно использовать только чтобы отмерять ровно 9 дм.
   1. Какие деления нужно восстановить, чтобы можно было одним прикладыванием отмерять целое количество дециметров от 1 до 9? Объясни, как отмерить отрезок 5 дм.
      Решение: Восстановим деления на 1, 2 и 6 дм. Пример измерения 5 дм: приложите начало линейки к концу отрезка, затем отметьте расстояние между метками 1 дм и 6 дм: $6 - 1 = 5$ дм. Полный набор измерений: - 1, 2, 3 (6–2–1), 4 (6–2), 5 (6–1), 6, 7 (9–2), 8 (9–1), 9 (конец линейки).
      Ответ: деления на 1, 2, 6 дм.
      
      
   2. Какое минимальное количество делений потребуется восстановить? Объясни, почему нельзя обойтись меньшим количеством, и покажи, как отмерить все 9 отрезков.
      Решение: Минимальное количество делений — 3 (1, 2, 6 дм). С двумя делениями невозможно получить все отрезки от 1 до 9: например, при наличии делений 1 и 4 дм, недостаёт 2, 6, 7 и других. С тремя делениями от 1 до 6 можно получить все комбинации.
      Ответ: 3 деления.