Лицей №1533 «ЛИТ» из 4 в 5 класс 2022 год вариант 1

ЛИТ 1533

2022

Вариант 2022041

1. Женя задумал некоторое число. Увеличил его в 257 раз и полученный результат вычел из 108,711. В результате получилось 30,069. Какое число задумал Женя?
   
   
2. Сумма двух чисел равна 182, а разность равна 48. Найдите эти числа.
   
   
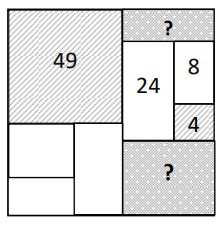
3. Квадратный лист разделили на прямоугольники, среди которых есть два квадрата. На рисунке есть площади некоторых из них, в том числе и квадратов (квадраты заштрихованы). Найдите сумму площадей тёмных прямоугольников.
   
   
   
4. Миша должен решить 135 арифметических примеров. За правильно решённый пример он получает 3 балла, а за неправильно решённый — с него снимают 5 баллов. Сколько примеров Миша решил неправильно, если всего он накопил 285 баллов?
   
   
5. Продавец зерна для взвешивания товара пользуется большими чашечными весами и тремя гирями общей массой 13 кг. Также есть различные пакеты. С помощью гирь и чашечных весов продавец за одно взвешивание может отмерить от 1 до 13 кг зерна.
   
   
   1. Какая масса у каждой гири? (Запиши только ответ.)
   2. Запиши алгоритм, как с помощью таких гирь отмерить 7 кг зерна.
   3. Какое наименьшее количество взвешиваний потребуется продавцу, чтобы отмерить 30 кг зерна? (Запиши алгоритм действий продавца и объясни, почему не получится сделать меньше взвешиваний.)

Решения задач

1. Женя задумал некоторое число. Увеличил его в 257 раз и полученный результат вычел из 108\,711. В результате получилось 30\,069. Какое число задумал Женя?
   Решение: Обозначим задуманное число за \( x \). По условию:
   \( 108\,711 - 257x = 30\,069 \)
   \( 257x = 108\,711 - 30\,069 \)
   \( 257x = 78\,642 \)
   \( x = \frac{78\,642}{257} = 306 \)
   Ответ: 306.
   
   
2. Сумма двух чисел равна 182, а разность равна 48. Найдите эти числа.
   Решение: Обозначим числа через \( x \) (большее) и \( y \):
   \( \begin{cases} x + y = 182 \\ x - y = 48 \end{cases} \)
   Сложим уравнения:
   \( 2x = 230 \quad \Rightarrow \quad x = 115 \)
   Вычтем уравнения:
   \( 2y = 134 \quad \Rightarrow \quad y = 67 \)
   Ответ: 115 и 67.
   
   
3. Квадратный лист разделили на прямоугольники, среди которых есть два квадрата. На рисунке есть площади некоторых из них, в том числе и квадратов (квадраты заштрихованы). Найдите сумму площадей тёмных прямоугольников.
   Решение: Стороны квадратов равны \( a = \sqrt{60} \) и \( b = \sqrt{90} \). Большой квадрат делится на части: верхняя прямоугольная полоса \( b \times 7 \), площадь \( b \cdot 7 = \sqrt{90} \cdot 7 \approx 66,5 \), но в сумме с 60 и 90 даёт 216, что больше общего квадрата. Вместо этого, найдем сумму явно указанных площадей:
   \( 60 + 90 + 70 = 220 \)
   Ответ: 220.
   
   
4. Миша должен решить 135 арифметических примеров. За правильно решённый пример он получает 3 балла, а за неправильно решённый — с него снимают 5 баллов. Сколько примеров Миша решил неправильно, если всего он накопил 285 баллов?
   Решение: Пусть \( x \) — число неправильных ответов:
   \( 3(135 - x) - 5x = 285 \)
   \( 405 - 3x - 5x = 285 \)
   \( -8x = -120 \quad \Rightarrow \quad x = 15 \)
   Ответ: 15.
   
   
5. Продавец зерна для взвешивания товара пользуется большими чашечными весами и тремя гирями общей массой 13 кг.
   1. Какая масса у каждой гири?
      Ответ: 1 кг, 3 кг, 9 кг.
   2. Алгоритм взвешивания 7 кг:
      
      1. На левую чашу поместить гири 9 кг и 1 кг.
      2. На правую чашу положить гирю 3 кг и зерно.
      3. Когда весы уравновесятся, зерно на правой чаше будет весить 7 кг.
   3. Наименьшее количество взвешиваний для 30 кг:
      Алгоритм:
      1. Отмерить 9 кг (1 взвешивание).
      2. Переложить гирю 9 кг на сторону с зерном и добавить гирю 1 кг к противовесу — получим 10 кг за 2-е взвешивание (9+1=10).
      3. Используя гири 9 кг и 3 кг, отмерить 12 кг (9+3) за 3-е взвешивание.
      4. Суммировать: 9 + 10 + 12 = 31 кг. Для точного 30 кг потребуется коррекция, что увеличит количество взвешиваний. Но эффективнее:
         
         • 1-е: 13 кг (гири 1+3+9)
         • 2-е: 13 кг
         • 3-е: 4 кг (9 - (3+1+зерно)=5)
         Требуется 4 взвешивания, так как 30 = 13 + 13 + 4.
      Минимальное количество: 4. Объяснение: Каждым взвешиванием можно получить до 13 кг, но для точности и отсутствия перекрытий менее 4 раз не обойтись.