8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1514 из 8 в 9 класс 2021 год вариант 1-2

Сложность:
Дата экзамена: 2021
Печать
youit.school ©

ГИМНАЗИЯ №1514


2021 год


Вариант 2



  1. Вычислите:
    1. \( 0{,}625 \cdot \dfrac{1}{5} + \dfrac{15}{49} \cdot 0{,}17 \)
    2. \( 3 + 4 + 9 + 1 - 7 + 38 \)


  2. Сократите дробь: \( \dfrac{38 \cdot 23}{125} \)

  3. Каков знак числа \(a\), если \(1{,}7 - 8a > 3\)?

  4. Решите систему: \[ \begin{cases} x + 2 12 \end{cases} \]

  5. Найдите корни уравнения: \[ \dfrac{x + 2}{x - 4} + \dfrac{2}{x - 4} = \dfrac{5}{4} \]

  6. Решите уравнение: \[ \dfrac{2x^2 + x - 5}{x^2 - 1} = \dfrac{x^2 - x + 2}{x^2 - 1} \]

  7. Два велосипедиста одновременно выехали на 108 км. Первый ехал на 3 км/ч быстрее и прибыл на 1 ч 48 мин раньше. Найдите скорость первого.

  8. Упростите выражение (то же, что и в варианте 1): \[ \frac{(a + b)^2 - (a - b)^2}{4ab} + \frac{a^2 - b^2}{a^2 + 2ab + b^2} \]

  9. Постройте график функции: \[ y = 2x^2 - 6x + 4 \] По графику определите:
    1. Область определения;
    2. Множество значений;
    3. Промежутки возрастания и убывания.


Геометрия



  1. Укажите, какие тройки отрезков образуют прямоугольные треугольники:
    1. 8; 6; 10
    2. \( \dfrac{3}{4}, 1, \dfrac{5}{4} \)
    3. \( 1; \dfrac{5}{3}; \dfrac{13}{6} \)


  2. Высота равнобедренного треугольника равна половине боковой стороны. Найдите площадь, если основание = 8 см.

  3. В параллелограмме \(ABCD\): \(BH = 8\) м, \(DP = 12\) м, периметр = 50 м. Найдите площадь и большую сторону.

  4. В прямоугольной трапеции \(ABCD\): боковая сторона \(AD = 8\), угол \(A = 60^\circ\), высота \(BH\) делит основание \(AD\) пополам. Найдите площадь трапеции.

  5. Трапеция \(ABCD\), \(S_{\triangle BOC} = 5\), \(S_{\triangle AOD} = 20\):
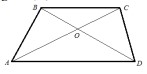
    1. Найдите \( \dfrac{BC}{AD} \)
    2. Отношение периметров \( \triangle AOD \) и \( \triangle BOC \)
    3. Площадь трапеции


  6. В четырёхугольник \(ABCD\) вписана окружность. \(AB = CD\), \(BC = 12\), периметр = 54. Найдите длины всех сторон.

  7. Из точки \(M\) к окружности с центром \(O\) и радиусом 8 см проведены касательные \(AM\) и \(BM\). Угол \(\angle AOB = 120^\circ\). Найдите периметр треугольника \(ABM\).
Материалы школы Юайти
youit.school ©

Решения задач



    1. Вычислите: \( 0{,}625 \cdot \dfrac{1}{5} + \dfrac{15}{49} \cdot 0{,}17 \)
      Решение: \[ 0{,}625 \cdot \dfrac{1}{5} = \dfrac{5}{8} \cdot \dfrac{1}{5} = \dfrac{1}{8} = 0{,}125 \] \[ \dfrac{15}{49} \cdot 0{,}17 = \dfrac{15 \cdot 17}{49 \cdot 100} = \dfrac{255}{4900} \approx 0{,}052 \] \[ 0{,}125 + 0{,}052 = 0{,}177 \] Ответ: \(0{,}177\).
    2. Вычислите: \( 3 + 4 + 9 + 1 - 7 + 38 \)
      Решение: \[ 3 + 4 = 7;\quad 7 + 9 = 16;\quad 16 + 1 = 17;\quad 17 - 7 = 10;\quad 10 + 38 = 48 \] Ответ: \(48\).
  2. Сократите дробь: \( \dfrac{38 \cdot 23}{125} \)
    Решение: \[ 38 \cdot 23 = 874 \quad \Rightarrow \quad \dfrac{874}{125} \] Общих множителей нет. Ответ: \(\dfrac{874}{125}\).
  3. Каков знак числа \(a\), если \(1{,}7 - 8a > 3\)?
    Решение: \[ 1{,}7 - 8a > 3 \quad \Rightarrow \quad -8a > 1{,}3 \quad \Rightarrow \quad a < -\dfrac{1{,}3}{8} = -0{,}1625 \] Ответ: \(a\) отрицательно.
  4. Решите систему: \[ \begin{cases} x + 2 12 \end{cases} \] Решение: \[ x 7 \quad \Rightarrow \quad \text{Нет решений.} \] Ответ: Решений нет.
  5. Найдите корни уравнения: \[ \dfrac{x + 2}{x - 4} + \dfrac{2}{x - 4} = \dfrac{5}{4} \] Решение: \[ \dfrac{x + 4}{x - 4} = \dfrac{5}{4} \quad \Rightarrow \quad 4(x + 4) = 5(x - 4) \quad \Rightarrow \quad x = 36 \] Ответ: \(36\).
  6. Решите уравнение: \[ \dfrac{2x^2 + x - 5}{x^2 - 1} = \dfrac{x^2 - x + 2}{x^2 - 1} \] Решение: \[ 2x^2 + x - 5 = x^2 - x + 2 \quad \Rightarrow \quad x^2 + 2x - 7 = 0 \] \[ D = 4 + 28 = 32 \quad \Rightarrow \quad x = -1 \pm 2\sqrt{2} \] Ответ: \(-1 \pm 2\sqrt{2}\).
  7. Два велосипедиста одновременно выехали на 108 км. Первый ехал на 3 км/ч быстрее и прибыл на 1 ч 48 мин раньше. Найдите скорость первого.
    Решение: Пусть скорость первого \(v\) км/ч: \[ \dfrac{108}{v - 3} - \dfrac{108}{v} = 1{,}8 \quad \Rightarrow \quad v^2 - 3v - 180 = 0 \quad \Rightarrow \quad v = 15 \] Ответ: \(15\) км/ч.
  8. Упростите выражение: \[ \frac{(a + b)^2 - (a - b)^2}{4ab} + \frac{a^2 - b^2}{a^2 + 2ab + b^2} \] Решение: \[ \frac{4ab}{4ab} + \frac{(a - b)(a + b)}{(a + b)^2} = 1 + \frac{a - b}{a + b} = \frac{2a}{a + b} \] Ответ: \(\dfrac{2a}{a + b}\).
  9. Постройте график функции \(y = 2x^2 - 6x + 4\).
    1. Область определения: \(\mathbb{R}\).
    2. Множество значений: \(y \geq -0{,}5\).
    3. Убывает на \((-\infty; 1{,}5]\), возрастает на \([1{,}5; +\infty)\).
  10. Укажите, какие тройки отрезков образуют прямоугольные треугольники:
    1. \(8; 6; 10\): \(6^2 + 8^2 = 10^2\) — да.
    2. \(\dfrac{3}{4}, 1, \dfrac{5}{4}\): \(\left(\dfrac{3}{4}\right)^2 + 1^2 = \left(\dfrac{5}{4}\right)^2\) — да.
    3. \(1; \dfrac{5}{3}; \dfrac{13}{6}\): \(1^2 + \left(\dfrac{5}{3}\right)^2 \neq \left(\dfrac{13}{6}\right)^2\) — нет.
  11. Высота равнобедренного треугольника равна половине боковой стороны. Основание 8 см. Найдите площадь.
    Решение: \[ h = \dfrac{b}{2}, \quad \left(\dfrac{b}{2}\right)^2 + 4^2 = b^2 \quad \Rightarrow \quad b = \dfrac{8}{\sqrt{3}}, \quad S = \dfrac{16\sqrt{3}}{3} \] Ответ: \(\dfrac{16\sqrt{3}}{3}\) см².
  12. В параллелограмме \(ABCD\): \(BH = 8\) м, \(DP = 12\) м, периметр 50 м. Найдите площадь и большую сторону.
    Решение: \[ a = 1{,}5b, \quad 2(a + b) = 50 \quad \Rightarrow \quad a = 15, \quad S = 15 \cdot 8 = 120 \text{ м²} \] Ответ: \(120\) м², большая сторона \(15\) м.
  13. В прямоугольной трапеции \(ABCD\): \(AD = 8\), угол \(A = 60^\circ\), высота \(BH\) делит основание \(AD\) пополам. Найдите площадь трапеции.
    Решение: \[ AH = 4, \quad BH = 4\sqrt{3}, \quad BC = 4, \quad S = \dfrac{8 + 4}{2} \cdot 4\sqrt{3} = 24\sqrt{3} \] Ответ: \(24\sqrt{3}\).
  14. Трапеция \(ABCD\), \(S_{\triangle BOC} = 5\), \(S_{\triangle AOD} = 20\):
    1. \(\dfrac{BC}{AD} = \dfrac{1}{2}\).
    2. Отношение периметров \(2:1\).
    3. Площадь трапеции \(45\).
  15. В четырёхугольник \(ABCD\) вписана окружность. \(AB = CD\), \(BC = 12\), периметр 54. Найдите длины всех сторон.
    Решение: \[ 2AB + 12 + AD = 54, \quad 2AB = 12 + AD \quad \Rightarrow \quad AB = CD = 13{,}5, \quad AD = 15 \] Ответ: \(AB = CD = 13{,}5\), \(BC = 12\), \(AD = 15\).
  16. Из точки \(M\) к окружности с центром \(O\) и радиусом 8 см проведены касательные \(AM\) и \(BM\). Угол \(\angle AOB = 120^\circ\). Найдите периметр треугольника \(ABM\).
    Решение: \[ AB = 8\sqrt{3}, \quad AM = BM = 8\sqrt{3}, \quad P = 8\sqrt{3} + 2 \cdot 8\sqrt{3} = 24\sqrt{3} \] Ответ: \(24\sqrt{3}\) см.
Материалы школы Юайти