8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1514 из 8 в 9 класс 2021 год вариант 1-1

Сложность:
Дата экзамена: 2021
Сложность:
Дата экзамена: 2021
youit.school ©

ГИМНАЗИЯ №1514


2021 год


Вариант 1



  1. Вычислите:
    1. \( 0{,}625 \cdot \dfrac{1}{5} + \dfrac{15}{49} \cdot 0{,}17 \)
    2. \( 3 + 4 + 9 + 1 - 7 + 38 \)


  2. Сократите дробь: \( \dfrac{6}{336} \cdot \dfrac{13}{35} \)

  3. Каков знак числа \(a\), если известно, что \(12 - 3a > 15\)?

  4. Решите систему неравенств: \[ \begin{cases} x + 4 13 \end{cases} \]

  5. Найдите корни уравнения: \[ \dfrac{x}{x + 3} - \dfrac{3}{x - 5} = \dfrac{x}{x^2 - 2x - 15} \]

  6. Решите уравнение: \[ \dfrac{2x^2 + 3x - 4}{x^2 + 2x - 3} = \dfrac{x^2 - 2x - 6}{x^2 + 2x - 3} \]

  7. Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ из 112 деталей на 4 часа быстрее. Сколько деталей в час делает второй рабочий?

  8. Упростите выражение: \[ \frac{(a + b)^2 - (a - b)^2}{4ab} + \frac{a^2 - b^2}{a^2 + 2ab + b^2} \]

  9. Постройте график функции: \[ y = -x^2 + 5x + 6 \] По графику определите:
    1. Область определения;
    2. Множество значений;
    3. Промежутки возрастания и убывания.


Геометрия



  1. Укажите, какие тройки отрезков образуют прямоугольные треугольники:
    1. 15; 39; 36
    2. \( \dfrac{3}{4}, 1, \dfrac{5}{3} \)
    3. 1; \( \dfrac{5}{3} \); \( \dfrac{7}{3} \)


  2. Высота равнобедренного треугольника равна половине боковой стороны. Найдите его площадь, если основание равно 6 дм.

  3. В параллелограмме \(ABCD\): \(CH = 6\) см, \(DP = 10\) см, периметр — 48 см. Найдите площадь и меньшую сторону.

  4. В прямоугольной трапеции \(ABCK\): боковая сторона \(CK = 23\), угол \(K = 45^\circ\), высота \(CH\) делит основание \(AK\) пополам. Найдите площадь трапеции.

  5. Дано: трапеция \(ABCD\), \(S_{\triangle BOC} = 3\) см², \(S_{\triangle AOD} = 27\) см².
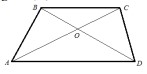
    1. Найдите \( \dfrac{BC}{AD} \)
    2. Найдите отношение периметров \( \triangle AOD \) и \( \triangle BOC \)
    3. Найдите площадь трапеции \(ABCD\)


  6. В четырёхугольник \(ABCD\) вписана окружность. Известно: \(AB = CD\), \(BC = 12\) см, периметр = 54 см. Найдите длины всех сторон.

  7. Хорды \(AB\) и \(CD\) пересекаются в точке \(M\). Известно: \(CM = 4\) см, \(DM = 9\) см, \(AM : MB = 4\). Найдите длину хорды \(AB\).
Материалы школы Юайти
youit.school ©

Решения задач



    1. Вычислите: \( 0{,}625 \cdot \dfrac{1}{5} + \dfrac{15}{49} \cdot 0{,}17 \)
      Решение:
      \(0{,}625 \cdot \dfrac{1}{5} = \dfrac{5}{8} \cdot \dfrac{1}{5} = \dfrac{1}{8} = 0{,}125\)
      \(\dfrac{15}{49} \cdot 0{,}17 = \dfrac{15 \cdot 17}{49 \cdot 100} = \dfrac{255}{4900} = \dfrac{51}{980} \approx 0{,}052\)
      Сумма: \(0{,}125 + 0{,}052 = 0{,}177\)
      Ответ: \(0{,}177\).
    2. Вычислите: \( 3 + 4 + 9 + 1 - 7 + 38 \)
      Решение:
      \(3 + 4 = 7\); \(7 + 9 = 16\); \(16 + 1 = 17\); \(17 - 7 = 10\); \(10 + 38 = 48\)
      Ответ: \(48\).
  2. Сократите дробь: \( \dfrac{6}{336} \cdot \dfrac{13}{35} \)
    Решение:
    \(\dfrac{6}{336} = \dfrac{1}{56}\)
    \(\dfrac{1}{56} \cdot \dfrac{13}{35} = \dfrac{13}{1960}\)
    Ответ: \(\dfrac{13}{1960}\).
  3. Каков знак числа \(a\), если известно, что \(12 - 3a > 15\)?
    Решение:
    \(12 - 3a > 15 \Rightarrow -3a > 3 \Rightarrow a < -1\)
    Ответ: \(a\) отрицательно.
  4. Решите систему неравенств: \[ \begin{cases} x + 4 13 \end{cases} \] Решение:
    \(x + 4 < 6 \Rightarrow x < 2\)
    \(x + 5 > 13 \Rightarrow x > 8\)
    Нет решений, так как \(x\) не может одновременно быть меньше 2 и больше 8.
    Ответ: Нет решений.
  5. Найдите корни уравнения: \[ \dfrac{x}{x + 3} - \dfrac{3}{x - 5} = \dfrac{x}{x^2 - 2x - 15} \] Решение:
    Общий знаменатель: \((x + 3)(x - 5)\)
    \(\dfrac{x(x - 5) - 3(x + 3)}{(x + 3)(x - 5)} = \dfrac{x}{(x + 3)(x - 5)}\)
    \(x^2 - 8x - 9 = x \Rightarrow x^2 - 9x - 9 = 0\)
    Дискриминант: \(D = 81 + 36 = 117\)
    Корни: \(x = \dfrac{9 \pm \sqrt{117}}{2}\)
    Ответ: \(\dfrac{9 \pm \sqrt{117}}{2}\).
  6. Решите уравнение: \[ \dfrac{2x^2 + 3x - 4}{x^2 + 2x - 3} = \dfrac{x^2 - 2x - 6}{x^2 + 2x - 3} \] Решение:
    Приравниваем числители:
    \(2x^2 + 3x - 4 = x^2 - 2x - 6 \Rightarrow x^2 + 5x + 2 = 0\)
    Дискриминант: \(D = 25 - 8 = 17\)
    Корни: \(x = \dfrac{-5 \pm \sqrt{17}}{2}\)
    Ответ: \(\dfrac{-5 \pm \sqrt{17}}{2}\).
  7. Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ из 112 деталей на 4 часа быстрее. Сколько деталей в час делает второй рабочий?
    Решение:
    Пусть второй делает \(x\) деталей/час, тогда первый — \(x + 9\).
    Время второго: \(\dfrac{112}{x}\), время первого: \(\dfrac{112}{x + 9}\)
    Уравнение: \(\dfrac{112}{x} - \dfrac{112}{x + 9} = 4\)
    Решение: \(x = 12\)
    Ответ: \(12\).
  8. Упростите выражение: \[ \frac{(a + b)^2 - (a - b)^2}{4ab} + \frac{a^2 - b^2}{a^2 + 2ab + b^2} \] Решение:
    Первое слагаемое: \(\dfrac{4ab}{4ab} = 1\)
    Второе слагаемое: \(\dfrac{(a - b)(a + b)}{(a + b)^2} = \dfrac{a - b}{a + b}\)
    Итог: \(1 + \dfrac{a - b}{a + b} = \dfrac{2a}{a + b}\)
    Ответ: \(\dfrac{2a}{a + b}\).
  9. Постройте график функции \(y = -x^2 + 5x + 6\).
    1. Область определения: \(x \in \mathbb{R}\)
    2. Множество значений: \(y \leq 12{,}25\)
    3. Промежутки возрастания: \((-\infty; 2{,}5)\), убывания: \((2{,}5; +\infty)\)
  10. Укажите, какие тройки отрезков образуют прямоугольные треугольники:
    1. \(15; 39; 36\): \(15^2 + 36^2 = 39^2\) — да.
    2. \(\dfrac{3}{4}, 1, \dfrac{5}{3}\): Нет.
    3. \(1; \dfrac{5}{3}; \dfrac{7}{3}\): Нет.
    Ответ: а).
  11. Высота равнобедренного треугольника равна половине боковой стороны. Основание 6 дм. Площадь:
    Решение:
    Боковая сторона \(b\), высота \(h = \dfrac{b}{2}\).
    По теореме Пифагора: \(\left(\dfrac{b}{2}\right)^2 + 3^2 = b^2 \Rightarrow b = 2\sqrt{3}\)
    Площадь: \(\dfrac{6 \cdot \sqrt{3}}{2} = 3\sqrt{3}\) дм².
    Ответ: \(3\sqrt{3}\) дм².
  12. В параллелограмме \(ABCD\): \(CH = 6\) см, \(DP = 10\) см, периметр 48 см.
    Решение:
    Стороны \(a\) и \(b\): \(2(a + b) = 48 \Rightarrow a + b = 24\)
    Площадь: \(6a = 10b \Rightarrow a = 15\), \(b = 9\)
    Ответ: площадь \(90\) см², меньшая сторона \(9\) см.
  13. В прямоугольной трапеции \(ABCK\): \(CK = 23\), угол \(K = 45^\circ\), высота \(CH\) делит основание \(AK\) пополам.
    Решение:
    \(CH = HK = \dfrac{23}{\sqrt{2}}\), \(AK = \dfrac{46}{\sqrt{2}}\)
    Площадь: \(\dfrac{(BC + AK)}{2} \cdot CH = \dfrac{69}{\sqrt{2}} \cdot \dfrac{23}{\sqrt{2}} = 396{,}75\) см².
    Ответ: \(396{,}75\) см².
  14. Трапеция \(ABCD\), \(S_{\triangle BOC} = 3\) см², \(S_{\triangle AOD} = 27\) см².
    1. \(\dfrac{BC}{AD} = \dfrac{1}{3}\)
    2. Отношение периметров: \(3:1\)
    3. Площадь трапеции: \(48\) см².
  15. Четырёхугольник \(ABCD\): \(AB = CD\), \(BC = 12\) см, периметр 54 см.
    Решение:
    \(AB = CD = 13{,}5\) см, \(AD = 15\) см.
    Ответ: \(AB = CD = 13{,}5\) см, \(BC = 12\) см, \(AD = 15\) см.
  16. Хорды \(AB\) и \(CD\) пересекаются в точке \(M\): \(CM = 4\) см, \(DM = 9\) см, \(AM : MB = 4:1\).
    Решение:
    \(AM \cdot MB = CM \cdot MD \Rightarrow 4x \cdot x = 36 \Rightarrow x = 3\)
    \(AB = 4x + x = 15\) см.
    Ответ: \(15\) см.
Материалы школы Юайти