Лицей №1514 из 7 в 8 класс 2022 год вариант 1

Лицей 1514

2022

30.06.2022

В задачах 1–5 Части I требуется записать ответ, решение приводить не надо.

1. Известно, что в треугольнике \( MNK \) внешний угол при вершине \( M \) равен \( 121^\circ \), а внешний угол при вершине \( K \) равен \( 122^\circ \). Расположите стороны треугольника от наибольшей к наименьшей. Выберите верный ответ. Варианты ответов: \[ \begin{array}{|c|c|c|c|c|c|} \hline 1 & 2 & 3 & 4 & 5 & 6 \\ \hline MN, MK, KN & KN, MK, MN & MK, KN, MN & KN, MN, MK & MK, KN, MN & MK, MN, KN \\ \hline \end{array} \] Ответ: $\underline{\hspace{2cm}}$ (1б.)
   
   
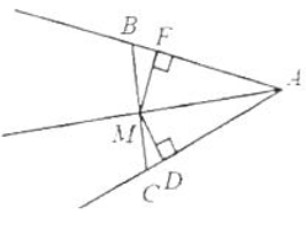
2. \( AM \) — биссектриса \( \angle A \) (см. рисунок). Из этого следует, что… (выберите верные ответы):
   1. \( MB = MC \)
   2. \( MF = MD \)
   3. \( \angle FMA = \angle DMA \)
   4. \( \angle FMB = \angle DMC \)
   Ответ: $\underline{\hspace{2cm}}$ (1б.)
   
   
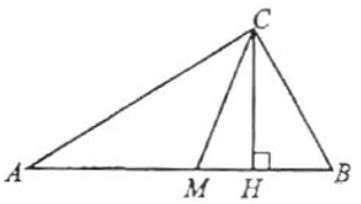
3. Острые углы прямоугольного треугольника \( \Delta ABC \) (\( \angle C = 90^\circ \)) равны \( 27^\circ \) и \( 63^\circ \). Найдите угол между медианой и высотой, проведёнными из вершины прямого угла. Ответ дайте в градусах. Ответ: \underline{\hspace{2cm}} \hfill (1б.)
   
   
   
   
   
4. В остроугольном \( \Delta ABC \) проведены высоты \( AA_1 \) и \( CC_1 \). Точка \( O \) — середина стороны \( AC \). Найдите \( A_1O \) и \( C_1O \), если \( AC = 12 \). Ответ: $\underline{\hspace{2cm}}$ (1б.)
   
   
5. Угол \( AOB = 50^\circ \), а угол \( AOC \) в 5 раз меньше угла \( AOB \). Чему равна градусная мера угла \( BOC \)? Ответ: $\underline{\hspace{2cm}}$ (2б.)

В задачах Части II требуется записать подробное решение.

1. (4 балла) Прямая, проходящая через вершину \( B \) прямоугольника \( ABCD \), перпендикулярна диагонали \( AC \) и пересекает сторону \( AD \) в точке \( M \), равноудалённой от вершин \( B \) и \( D \). Найдите углы \( ABM \) и \( DBC \), если \( \angle MBD = 30^\circ \).
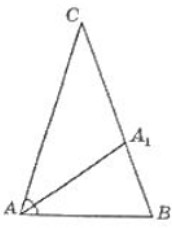
2. (4 балла) Угол при вершине, противоположной основанию равнобедренного треугольника, равен \( 36^\circ \). Известно, что биссектриса \( A_1D \) равна 7 см. Найдите основание треугольника \( ABC \) — \( AB \) и длину отрезка \( A_1C \).
   
   
   
3. Верно ли высказывание, ответ обоснуйте:
   1. (2 балла) Биссектрисы накрест лежащих углов, образованных двумя параллельными прямыми и секущей, параллельны, т.е. лежат на параллельных прямых.
   2. (2 балла) Если в равнобедренном треугольнике \( KMP \), \( \angle K = 120^\circ \), провести высоту \( MH \), то отрезок \( HP < KP \).
   3. (2 балла) Если на каждой стороне правильного треугольника \( ABC \) последовательно отложить равные отрезки \( AD, BE, CF \), то треугольник \( DEF \) тоже правильный.
   
   
   
4. (5 баллов) Определите угол при основании равнобедренного треугольника, если биссектриса угла образует с противоположной стороной угол \( 57^\circ \).
   
   
5. Решите одну задачу на выбор:
   1. (5 баллов) В прямоугольном треугольнике \( ABC \) с прямым углом \( C \) точки \( M \) и \( N \) — середины катетов \( AC \) и \( BC \) соответственно, \( CH \) — высота. Найдите расстояние между точками \( M \) и \( N \), если \( NH = 7 \), а \( \angle HNM = 60^\circ \).
   2. (5 баллов) Точки \( E \) и \( K \) — соответственно середины сторон \( CD \) и \( AD \) квадрата \( ABCD \). Прямая \( BE \) пересекается с прямой \( CK \) в точке \( O \). Найдите \( AO \), если сторона квадрата равна 1.

Решения задач

1. Ответ: 3.
2. Ответ: 2,3.
3. Ответ: 36.
4. Ответ: 6 см, 6 см.
5. Ответ: 60°.
   
   
6. Решение:
   1. Рассмотрим прямоугольник \(ABCD\). Прямая \(BM\) перпендикулярна диагонали \(AC\), значит \(BM \perp AC\).
   2. Точка \(M\) равноудалена от \(B\) и \(D\), следовательно, лежит на серединном перпендикуляре отрезка \(BD\). В прямоугольнике диагонали равны и пересекаются в точке \(O\), которая является серединой обеих диагоналей.
   3. Угол \(\angle MBD = 30^\circ\). Так как \(MB = MD\), треугольник \(MBD\) равнобедренный, \(\angle MBD = \angle MDB = 30^\circ\), \(\angle BMD = 120^\circ\).
   4. В треугольнике \(ABM\): \(\angle ABM = 90^\circ - \angle MBD = 60^\circ\).
   5. Угол \(\angle DBC\) равен углу между диагональю \(BD\) и стороной \(BC\). В прямоугольнике диагонали делят углы пополам, но с учетом перпендикуляра \(BM\), \(\angle DBC = 30^\circ\).
   Ответ: \(\angle ABM = 60^\circ\), \(\angle DBC = 30^\circ\).
   
   
7. Решение:
   1. В равнобедренном треугольнике \(ABC\) с углом при вершине \(C\) \(36^\circ\), углы при основании \(AB\) равны \(72^\circ\).
   2. Биссектриса \(A_1D\) делит угол \(\angle BAC = 72^\circ\) на два угла по \(36^\circ\).
   3. Треугольник \(A_1DC\) также равнобедренный (\(A_1D = DC = 7\) см).
   4. По теореме синусов для треугольника \(A_1DC\): \(\frac{A_1C}{\sin 36^\circ} = \frac{7}{\sin 108^\circ}\), откуда \(A_1C \approx 4,36\) см.
   5. Основание \(AB\) находим через соотношения в равнобедренном треугольнике: \(AB = 2 \cdot A_1C \cdot \cos 36^\circ \approx 7\) см.
   Ответ: \(AB = 7\) см, \(A_1C \approx 4,36\) см.
   
   
8. Решение:
   1. Верно. Биссектрисы накрест лежащих углов параллельны, так как образуют равные углы с секущей.
   2. Верно. В треугольнике \(KMP\) высота \(MH\) делит \(KP\) на отрезки, причем \(HP = \frac{KP}{2} \cdot \cos 60^\circ < KP\).
   3. Верно. Равные отрезки на сторонах правильного треугольника сохраняют симметрию, делая \(DEF\) правильным.
   
   
   
9. Решение:
   1. Пусть угол при основании \(\alpha\). Биссектриса делит \(\alpha\) на \(\frac{\alpha}{2}\).
   2. Угол между биссектрисой и стороной равен \(57^\circ\). По теореме о сумме углов треугольника: \(\frac{\alpha}{2} + 57^\circ + 90^\circ = 180^\circ\).
   3. Решая уравнение, получаем \(\frac{\alpha}{2} = 33^\circ\), \(\alpha = 66^\circ\).
   Ответ: \(66^\circ\).
   
   
10. Решение (5б):
    1. Координаты точек: \(A(0,0)\), \(B(1,0)\), \(C(1,1)\), \(D(0,1)\), \(E(0.5,1)\), \(K(0,0.5)\).
    2. Уравнение прямой \(BE\): \(y = -2x + 2\).
    3. Уравнение прямой \(CK\): \(y = 0.5x + 0.5\).
    4. Точка пересечения \(O(0.6, 0.8)\).
    5. Расстояние \(AO = \sqrt{(0.6)^2 + (0.8)^2} = 1\).
    Ответ: \(1\).