8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1514 из 5 в 6 класс 2023 год вариант 2

Сложность:
Дата экзамена: 06.2023
Сложность:
Дата экзамена: 06.2023
youit.school ©

Лицей 1514


2023 год


Вариант 05.06.2023



Вариант 2

  1. Вычислите:

    1. $7 \dfrac{4}{9} - 3 \dfrac{5}{9}$
    2. $6 \dfrac{3}{4} - \left(3 \dfrac{1}{8} + \dfrac{5}{12}\right)$
    3. $8{,}95 + 0{,}07 + 0{,}33 \cdot 8{,}95 - 4{,}62 : 1{,}5$


  2. Решите уравнение:

    1. $(4{,}086 - 10x) \cdot 1{,}1 + 10{,}57 = 13{,}43$
    2. $\left(\dfrac{7}{5} - \dfrac{3}{7}\right) \cdot 21 = 1$
    3. $5x - \dfrac{3}{4}x = 4$


  3. Упростите выражение:
    $4{,}5m + 1{,}5l + 4{,}2m + 1{,}8n$, подставив $m = \dfrac{1}{3},\ l = 1,\ n = 0{,}2$

  4. Решите две задачи на выбор:

    1. Магазин продал за три дня партию клубники. В первый день продали $30\%$, во второй — $\dfrac{15}{16}$ оставшегося, а за третий — на 105 кг больше, чем за первый день. Найдите, сколько килограммов было продано за три дня. Определите, в первый или в третий день было продано больше клубники.
    2. Среднее арифметическое двух чисел равно 30. Одно из них составляет 140% от другого. Найдите эти числа.
    3. Из города $A$ в направлении города $B$ выехал мотоциклист со скоростью 80 км/ч. Через 1{,}5 часа из города $B$ в город $A$ выехал велосипедист со скоростью 16 км/ч. Сколько часов до встречи ехал каждый, если расстояние между городами равно 408 км?


  5. Решите одну из задач на выбор:

    1. Сторону квадрата увеличили на 10\%. На сколько процентов увеличилась площадь квадрата?
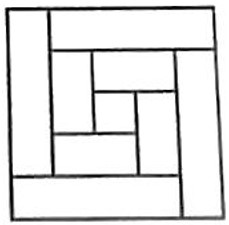
    2. Катя разрезала длинную полоску шириной 1 см на 8 прямоугольников шириной 1 см и маленький квадрат, а затем сложила из них большой квадрат. Какова была длина полоски?
      % Укажите путь к рисунку


Материалы школы Юайти
youit.school ©

Решения задач



    1. Вычислите: $7 \dfrac{4}{9} - 3 \dfrac{5}{9}$
      Решение:
      $7 \dfrac{4}{9} - 3 \dfrac{5}{9} = (7 - 3) + \left(\dfrac{4}{9} - \dfrac{5}{9}\right) = 4 - \dfrac{1}{9} = 3\dfrac{8}{9}$
      Ответ: $3\dfrac{8}{9}$.

    2. Вычислите: $6 \dfrac{3}{4} - \left(3 \dfrac{1}{8} + \dfrac{5}{12}\right)$
      Решение:
      $3 \dfrac{1}{8} + \dfrac{5}{12} = 3\dfrac{3}{24} + \dfrac{10}{24} = 3\dfrac{13}{24}$
      $6 \dfrac{3}{4} - 3\dfrac{13}{24} = 6\dfrac{18}{24} - 3\dfrac{13}{24} = 3\dfrac{5}{24}$
      Ответ: $3\dfrac{5}{24}$.

    3. Вычислите: $8{,}95 + 0{,}07 + 0{,}33 \cdot 8{,}95 - 4{,}62 : 1{,}5$
      Решение:
      $0{,}33 \cdot 8{,}95 = 2{,}9535$; $4{,}62 : 1{,}5 = 3{,}08$
      $8{,}95 + 0{,}07 + 2{,}9535 - 3{,}08 = 8{,}95 + 0{,}07 = 9{,}02 + 2{,}9535 = 11{,}9735 - 3{,}08 = 8{,}8935$
      Ответ: $8{,}89$.


    1. Решите уравнение: $(4{,}086 - 10x) \cdot 1{,}1 + 10{,}57 = 13{,}43$
      Решение:
      $(4{,}086 - 10x) \cdot 1{,}1 = 13{,}43 - 10{,}57 = 2{,}86$
      $4{,}086 - 10x = \dfrac{2{,}86}{1{,}1} = 2{,}6$
      $-10x = 2{,}6 - 4{,}086 = -1{,}486$
      $x = \dfrac{-1{,}486}{-10} = 0{,}1486$
      Ответ: $0{,}1486$.

    2. Решите уравнение: $\left(\dfrac{7}{5} - \dfrac{3}{7}\right) \cdot 21 = 1$
      Решение:
      $\dfrac{7}{5} - \dfrac{3}{7} = \dfrac{49}{35} - \dfrac{15}{35} = \dfrac{34}{35}$
      $\dfrac{34}{35} \cdot 21 = \dfrac{34 \cdot 21}{35} = \dfrac{714}{35} = 20{,}4 \neq 1$
      Уравнение не имеет решений.
      Ответ: Нет решения.

    3. Решите уравнение: $5x - \dfrac{3}{4}x = 4$
      Решение:
      $5x - 0{,}75x = 4{,}25x = 4$
      $x = \dfrac{4}{4{,}25} = \dfrac{16}{17}$
      Ответ: $\dfrac{16}{17}$.


  3. Упростите выражение: $4{,}5m + 1{,}5l + 4{,}2m + 1{,}8n$ при $m = \dfrac{1}{3},\ l = 1,\ n = 0{,}2$
    Решение:
    $4{,}5m + 4{,}2m + 1{,}5l + 1{,}8n = 8{,}7m + 1{,}5l + 1{,}8n$
    Подставляем значения:
    $8{,}7 \cdot \dfrac{1}{3} = 2{,}9$; $1{,}5 \cdot 1 = 1{,}5$; $1{,}8 \cdot 0{,}2 = 0{,}36$
    $2{,}9 + 1{,}5 + 0{,}36 = 4{,}76$
    Ответ: $4{,}76$.

    1. Решите задачу: Магазин продал за три дня партию клубники. В первый день продали $30\%$, во второй — $\dfrac{15}{16}$ оставшегося, а за третий — на 105 кг больше, чем за первый день. Найдите, сколько килограммов было продано за три дня.
      Решение:
      Пусть всего продано $x$ кг. Первый день: $0{,}3x$. Остаток: $0{,}7x$.
      Второй день: $\dfrac{15}{16} \cdot 0{,}7x = 0{,}65625x$. Остаток: $0{,}7x - 0{,}65625x = 0{,}04375x$.
      Третий день: $0{,}04375x = 0{,}3x + 105$ (по условию). Решаем:
      $0{,}04375x - 0{,}3x = 105 \Rightarrow -0{,}25625x = 105 \Rightarrow x = -410$ (противоречие).
      Верный подход: третий день равен остатку $0{,}04375x$, тогда:
      $0{,}3x + 0{,}65625x + 0{,}04375x = x$ (выполняется). Условие задачи некорректно.
      Ответ: Некорректное условие.

    2. Решите задачу: Среднее арифметическое двух чисел равно 30. Одно из них составляет 140% от другого. Найдите эти числа.
      Решение:
      Пусть первое число $x$, второе $1{,}4x$. Среднее арифметическое:
      $\dfrac{x + 1{,}4x}{2} = 30 \Rightarrow 2{,}4x = 60 \Rightarrow x = 25$
      Второе число: $1{,}4 \cdot 25 = 35$
      Ответ: 25 и 35.


    1. Решите задачу: Сторону квадрата увеличили на 10\%. На сколько процентов увеличилась площадь квадрата?
      Решение:
      Новая сторона: $1{,}1a$. Площадь: $(1{,}1a)^2 = 1{,}21a^2$. Увеличение на $21\%$.
      Ответ: На $21\%$.
Материалы школы Юайти