8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1514 из 5 в 6 класс 2023 год вариант 1

Сложность:
Дата экзамена: 06.2023
Сложность:
Дата экзамена: 06.2023
youit.school ©

Лицей 1514


2023 год


Вариант 05.06.2023



Вариант 1

  1. Вычислите:

    1. $\dfrac{5}{12} + \dfrac{5}{12} - \dfrac{7}{15}$
    2. $\left(\dfrac{7}{14} + \dfrac{5}{21}\right) \cdot \dfrac{3}{7}$
    3. $3{,}84 \cdot 3{,}2 - 3{,}84 \cdot 1{,}7 = 4{,}27 \cdot 1{,}4$


  2. Решите уравнение:

    1. $(10x + 1{,}086) \cdot 0{,}6 + 12{,}52 = 16{,}48$
    2. $\left(\dfrac{5}{7} + \dfrac{3}{4}\right) \cdot 15 = 8$
    3. $3x - \dfrac{2}{5}x = 3$


  3. Упростите выражение:
    $3{,}7x + 2{,}3y + 1{,}6x + 8{,}4y$ и вычислите при $x = \dfrac{1}{4},\ y = 0{,}5$

  4. Решите две задачи на выбор:

    1. Магазин продал за три дня партию яблок. В первый день было продано $30\%$ массы яблок, во второй — $60\%$ оставшегося, в третий — на 8 кг больше, чем во второй день. Найдите, сколько килограммов было продано за три дня, если во второй день продали 6 кг? В какой из трёх дней продано больше всего?
    2. Среднее арифметическое двух чисел равно 11. Первое из них составляет $45\%$ от другого. Найдите эти числа.
    3. Из первого города во второй выехал автомобиль со скоростью 65 км/ч, а через $1{,}5$ часа после этого из второго города навстречу ему выехал второй автомобиль со скоростью 75 км/ч. Найдите время, которое проехал первый автомобиль до момента встречи, если расстояние между городами равно 690 км.


  5. Решите одну из задач на выбор:

    1. Одну из сторон прямоугольника увеличили на 25%. На сколько процентов надо уменьшить другую сторону, чтобы площадь прямоугольника не изменилась?
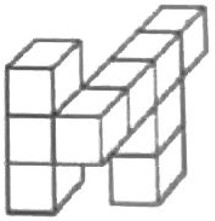
    2. Прямоугольный параллелепипед был сложен из кубиков со стороной 1. Когда несколько из них отвалились, осталась фигура, изображённая на рисунке. Какие имелись размеры у параллелепипеда? Сколько кубиков от него отвалилось?
      Укажите правильный путь


Материалы школы Юайти
youit.school ©

Решения задач



    1. Вычислите: $\dfrac{5}{12} + \dfrac{5}{12} - \dfrac{7}{15}$
      Решение:
      $\dfrac{5}{12} + \dfrac{5}{12} = \dfrac{10}{12} = \dfrac{5}{6}$
      $\dfrac{5}{6} - \dfrac{7}{15} = \dfrac{25}{30} - \dfrac{14}{30} = \dfrac{11}{30}$
      Ответ: $\dfrac{11}{30}$.

    2. Вычислите: $\left(\dfrac{7}{14} + \dfrac{5}{21}\right) \cdot \dfrac{3}{7}$
      Решение:
      $\dfrac{7}{14} = \dfrac{1}{2}$; $\dfrac{5}{21}$ остается
      $\dfrac{1}{2} + \dfrac{5}{21} = \dfrac{21}{42} + \dfrac{10}{42} = \dfrac{31}{42}$
      $\dfrac{31}{42} \cdot \dfrac{3}{7} = \dfrac{93}{294} = \dfrac{31}{98}$
      Ответ: $\dfrac{31}{98}$.

    3. Вычислите: $3{,}84 \cdot 3{,}2 - 3{,}84 \cdot 1{,}7 + 4{,}27 \cdot 1{,}4$
      Решение:
      $3{,}84 \cdot (3{,}2 - 1{,}7) = 3{,}84 \cdot 1{,}5 = 5{,}76$
      $4{,}27 \cdot 1{,}4 = 5{,}978$
      $5{,}76 + 5{,}978 = 11{,}738$
      Ответ: $11{,}738$.


    1. Решите уравнение: $(10x + 1{,}086) \cdot 0{,}6 + 12{,}52 = 16{,}48$
      Решение:
      $(10x + 1{,}086) \cdot 0{,}6 = 16{,}48 - 12{,}52 = 3{,}96$
      $10x + 1{,}086 = \dfrac{3{,}96}{0{,}6} = 6{,}6$
      $10x = 6{,}6 - 1{,}086 = 5{,}514$
      $x = \dfrac{5{,}514}{10} = 0{,}5514$
      Ответ: $0{,}5514$.

    2. Решите уравнение: $\left(\dfrac{5}{7} + \dfrac{3}{4}\right) \cdot 15 = 8$
      Решение:
      $\dfrac{5}{7} + \dfrac{3}{4} = \dfrac{20}{28} + \dfrac{21}{28} = \dfrac{41}{28}$
      $\dfrac{41}{28} \cdot 15 = \dfrac{615}{28}$
      $\dfrac{615}{28}x = 8 \quad \Rightarrow \quad x = 8 \cdot \dfrac{28}{615} = \dfrac{224}{615}$
      Ответ: $\dfrac{224}{615}$.

    3. Решите уравнение: $3x - \dfrac{2}{5}x = 3$
      Решение:
      $\dfrac{15x - 2x}{5} = 3 \quad \Rightarrow \quad \dfrac{13x}{5} = 3$
      $x = \dfrac{15}{13} = 1 \dfrac{2}{13}$
      Ответ: $1 \dfrac{2}{13}$.


  3. Упростите выражение: $3{,}7x + 2{,}3y + 1{,}6x + 8{,}4y$ и вычислите при $x = \dfrac{1}{4},\ y = 0{,}5$
    Решение:
    $3{,}7x + 1{,}6x = 5{,}3x$; $2{,}3y + 8{,}4y = 10{,}7y$
    $5{,}3 \cdot \dfrac{1}{4} + 10{,}7 \cdot 0{,}5 = 1{,}325 + 5{,}35 = 6{,}675$
    Ответ: $6{,}675$.

    1. Задача а:
      Решение:
      Во второй день продано 6 кг — 60% от остатка после первого дня:
      Остаток после первого дня: $\dfrac{6}{0{,}6} = 10$ кг
      Первый день: $30\%$ от общего количества, значит $70% = 10$ кг
      Общее количество: $\dfrac{10}{0{,}7} \approx 14{,}29$ кг
      Третий день: $6 + 8 = 14$ кг
      Всего продано: $14{,}29 \cdot 0{,}3 + 6 + 14 \approx 4{,}29 + 6 + 14 = 24{,}29$ кг
      Наибольшая продажа в третий день.
      Ответ: $24{,}29$ кг, третий день.

    2. Задача б:
      Решение:
      Среднее арифметическое: $\dfrac{a + b}{2} = 11 \quad \Rightarrow \quad a + b = 22$
      Первое число составляет $45\%$ от второго: $a = 0{,}45b$
      $0{,}45b + b = 22 \quad \Rightarrow \quad 1{,}45b = 22 \quad \Rightarrow \quad b \approx 15{,}17$
      $a = 22 - 15{,}17 \approx 6{,}83$
      Ответ: $6{,}83$ и $15{,}17$.

    3. Задача в:
      Решение:
      Пусть время первого автомобиля до встречи — $t$ часов
      Второй автомобиль ехал $t - 1{,}5$ часов
      Расстояние: $65t + 75(t - 1{,}5) = 690$
      $65t + 75t - 112{,}5 = 690 \quad \Rightarrow \quad 140t = 802{,}5 \quad \Rightarrow \quad t \approx 5{,}73$ часа
      Ответ: $5{,}73$ часа.


    1. Задача а:
      Решение:
      Пусть стороны $a$ и $b$. Площадь до изменений: $S = ab$
      После увеличения одной стороны на $25\%$: $a' = 1{,}25a$
      Новая площадь: $1{,}25a \cdot b' = ab \quad \Rightarrow \quad b' = \dfrac{ab}{1{,}25a} = 0{,}8b$
      Уменьшение на $20\%$
      Ответ: на $20\%$.

    2. Задача б:
      Решение:
      Исходный параллелепипед: $4 \times 3 \times 3$ (объём 36 кубиков)
      Оставшиеся кубики: 27 (по рисунку)
      Отвалилось: $36 - 27 = 9$ кубиков
      Ответ: размеры $4 \times 3 \times 3$, отвалилось 9 кубиков.
Материалы школы Юайти