Лицей №1514 из 5 в 6 класс 2022 год вариант 1

Лицей 1514

2022 год

09.06.2022

1. Вычислите:
   1. \( \left( 2 \dfrac{14}{27} : 4 \dfrac{2}{15} \right) \times \dfrac{1}{4} \)
   2. \( 47.5 : (21.7 \cdot 0.1 + 5.43) + 74.778 : 72.6 - 71.6 \)
2. Решите уравнение:
   1. \( x + \dfrac{3}{5} - \dfrac{3}{5} = \dfrac{3}{5} \)
   2. \( 0.7a - 0.3(1.4 + a) = 0.0158 : 0.01 \)
3. Расстояние между деревнями Кротово и Ванино равно 300 км по просёлочной дороге. Из деревень одновременно выехали навстречу друг другу два автомобиля. Через два часа они ещё не встретились и между ними было 59 км. С какой скоростью ехал каждый из них, если скорость первого на 10{,}5 км/ч меньше скорости второго?
4. Упростите выражение:
   1. \( (258b + 87) \cdot 0.01 - 2.42b + 0.13 \)
   2. \( \dfrac{7}{10}k + 1.4k - \dfrac{5}{6}k = 1.2 \)
   Найдите значение этого выражения при \( k = 4.5 \).
5. В автобусной экскурсии участвовали учащиеся 5–7 классов, причём пятиклассников было 180, что составляло \(0.36\) всех учащихся, а \( \dfrac{5}{8} \) оставшихся ребят были шестиклассниками. Для 5 классов, 6 классов и 7 классов были взяты автобусы вместимостью 45, 40 и 30 человек соответственно. Сколько потребовалось автобусов каждого типа?
   
   
6. [6*.] Решите одну из трёх задач на выбор:
   1. Книга стоит 120 рублей и ещё \( \dfrac{3}{4} \) её стоимости. Сколько стоит книга?
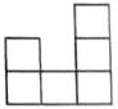
   2. Можно ли прямоугольник \( 7 \times 12 \) разрезать на фигурки вида
      

Решения задач

1. 1. Вычислите: \( \left( 2 \dfrac{14}{27} : 4 \dfrac{2}{15} \right) \times \dfrac{1}{4} \)
      Решение:
      Переведём смешанные числа в неправильные дроби:
      \( 2\dfrac{14}{27} = \dfrac{68}{27} \), \( 4\dfrac{2}{15} = \dfrac{62}{15} \)
      Выполним деление:
      \( \dfrac{68}{27} : \dfrac{62}{15} = \dfrac{68}{27} \times \dfrac{15}{62} = \dfrac{34 \times 5}{27 \times 31} = \dfrac{170}{837} \)
      Умножим на \(\dfrac{1}{4}\):
      \( \dfrac{170}{837} \times \dfrac{1}{4} = \dfrac{85}{558} \)
      Ответ: \(\dfrac{85}{558}\).
      
      
   2. Вычислите: \( 47.5 : (21.7 \cdot 0.1 + 5.43) + 74.778 : 72.6 - 71.6 \)
      Решение:
      Вычислим выражение в скобках:
      \( 21.7 \cdot 0.1 = 2.17 \), \( 2.17 + 5.43 = 7.6 \)
      Разделим:
      \( 47.5 : 7.6 = 6.25 \), \( 74.778 : 72.6 \approx 1.03 \)
      Сложим и вычтем:
      \( 6.25 + 1.03 - 71.6 = -64.32 \)
      Ответ: \(-64.32\).
   
   
   
2. 1. Решите уравнение: \( x + \dfrac{3}{5} - \dfrac{3}{5} = \dfrac{3}{5} \)
      Решение:
      \( x + \dfrac{3}{5} - \dfrac{3}{5} = \dfrac{3}{5} \)
      \( x = \dfrac{3}{5} \)
      Ответ: \( \dfrac{3}{5} \).
      
      
   2. Решите уравнение: \( 0.7a - 0.3(1.4 + a) = 0.0158 : 0.01 \)
      Решение:
      \( 0.0158 : 0.01 = 1.58 \)
      Раскроем скобки:
      \( 0.7a - 0.42 - 0.3a = 1.58 \)
      \( 0.4a - 0.42 = 1.58 \)
      \( 0.4a = 2 \)
      \( a = 5 \)
      Ответ: \(5\).
   
   
   
3. Расстояние между деревнями Кротово и Ванино равно 300 км. Автомобили проехали вместе \(300 - 59 = 241\) км за 2 часа. Их общая скорость:
   \( \dfrac{241}{2} = 120.5 \) км/ч.
   Пусть скорость первого автомобиля \(x\), тогда второго \(x + 10.5\):
   \( x + x + 10.5 = 120.5 \)
   \( 2x = 110 \)
   \( x = 55 \) км/ч (первый автомобиль)
   \( x + 10.5 = 65.5 \) км/ч (второй автомобиль)
   Ответ: \(55\) км/ч и \(65.5\) км/ч.
   
   
4. 1. Упростите выражение: \( (258b + 87) \cdot 0.01 - 2.42b + 0.13 \)
      Решение:
      \( 2.58b + 0.87 - 2.42b + 0.13 = 0.16b + 1 \)
      Ответ: \(0.16b + 1\).
      
      
   2. Найдите значение выражения при \( k = 4.5 \):
      \( 0.16 \cdot 4.5 + 1 = 0.72 + 1 = 1.72 \)
      Ответ: \(1.72\).
   
   
   
5. Всего учащихся: \( \dfrac{180}{0.36} = 500 \)
   Шестиклассники: \( (500 - 180) \cdot \dfrac{5}{8} = 200 \)
   Семиклассники: \( 500 - 180 - 200 = 120 \)
   Автобусы:
   5 класс: \( \dfrac{180}{45} = 4 \)
   6 класс: \( \dfrac{200}{40} = 5 \)
   7 класс: \( \dfrac{120}{30} = 4 \)
   Ответ: 4, 5, 4.
   
   
6. [6*.]
   1. Книга стоит \(x\) рублей:
      \( x = 120 + \dfrac{3}{4}x \)
      \( \dfrac{1}{4}x = 120 \)
      \( x = 480 \)
      Ответ: 480 рублей.
      
      
   2. Площадь прямоугольника \(7 \times 12 = 84\). Фигурка занимает 4 клетки. \(84\) делится на \(4\), но из-за формы фигурки (уголок) невозможно покрыть прямоугольник без наложений или пробелов.
      Ответ: Нельзя.