Лицей №1514 из 4 в 5 класс 2025 год вариант 1
Печать
youit.school ©
Лицей 1514
2025 год
15.03.2025
- Вычислите: $5555+(82320: 84-693) \cdot 66$
- Решите уравнение: $(65: x+25 \cdot 5): 13=10$
- Вычислите: 3 м 505 мм -1 м 2 дм +325 см. Дайте ответ в м, дм, см и мм.
- Первый поезд вышел из города $A$ в 10:00 и прибыл в город $B$ в 16 часов 5 минут. Второй поезд вышел из $A$ на полчаса позже первого поезда и прибыл в $B$ на 25 минут раньше первого поезда. Сколько минут был в пути второй поезд?
- На доске написано число. Саша его умножил на 6, к результату прибавил 18 и получил число в 7 раз меньшее, чем 210 . Какое число записано на доске?
- В 8.00 из пункта А в пункт В, расстояние между которыми 540 км, выехал автомобиль. В это же время навстречу ему из пункта В выехал мотоциклист. Скорость мотоциклиста на 20 км/ч больше скорости автомобиля. Найдите скорости автомобиля и мотоциклиста, если в 10 часов утра им оставалось до встречи 180 км.
- Мастер на первую часть задания затратил 2 часа, а на вторую часть задания -3 часа. Всего за 5 часов он сделал 390 деталей. С какой производительностью работал мастер первые 2 часа, если его производительность в последние 3 часа была на 30 деталей в час больше, чем при выполнении первой части задания?
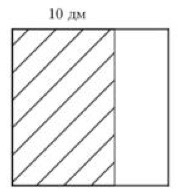
- От квадратного листа фанеры, периметр которого 6 м, отпилили кусок шириной 10 дм (см рисунок). Найдите площадь и периметр оставшейся части.
- Квадрат с площадью 81 дм$^2$ разрезали на четыре одинаковых квадрата, которые выложили в одну полосу (получился узкий длинный прямоугольник). Найдите периметр этого прямоугольника.
- Нина записала все числа от 1 до 110 , включая 1 и 110 . Сколько раз она написала цифру 1?
- За один день работы гном может добыть 5, 7 или 11 драгоценных камней. Сможет ли гном за 9 дней работы добыть ровно 70 драгоценных камней? Если да, то как? Если нет - докажите, что не сможет.
Материалы школы Юайти
youit.school ©
Решения задач
- Вычислите: $5555+(82320: 84-693) \cdot 66$
Решение:
$82320 : 84 = 980$
$980 - 693 = 287$
$287 \cdot 66 = 18942$
$5555 + 18942 = 24497$
Ответ: 24497.
- Решите уравнение: $(65: x+25 \cdot 5): 13=10$
Решение:
$(65 : x + 125) : 13 = 10$
$65 : x + 125 = 130$
$65 : x = 5$
$x = 65 : 5 = 13$
Ответ: 13.
- Вычислите: 3 м 505 мм -1 м 2 дм +325 см. Дайте ответ в м, дм, см и мм.
Решение:
3 м 505 мм = 3505 мм
1 м 2 дм = 1200 мм
325 см = 3250 мм
$3505 - 1200 + 3250 = 5555$ мм
Переводим: 5,555 м 55,55 дм 555,5 см 5555мм
Ответ: 5,555 м 55,55 дм 555,5 см 5555мм .
- Первый поезд вышел из города $A$ в 10:00 и прибыл в город $B$ в 16 часов 5 минут. Второй поезд вышел из $A$ на полчаса позже первого поезда и прибыл в $B$ на 25 минут раньше первого поезда. Сколько минут был в пути второй поезд?
Решение:
Время пути второго поезда: с 10:30 до 15:40
$15:40 - 10:30 = 5$ часов $10$ минут = $310$ минут
Ответ: 310.
- На доске написано число. Саша его умножил на 6, к результату прибавил 18 и получил число в 7 раз меньшее, чем 210. Какое число записано на доске?
Решение:
$210 : 7 = 30$
$30 - 18 = 12$
$12 : 6 = 2$
Ответ: 2.
- В 8.00 из пункта А в пункт В, расстояние между которыми 540 км, выехал автомобиль. В это же время навстречу ему из пункта В выехал мотоциклист. Скорость мотоциклиста на 20 км/ч больше скорости автомобиля. Найдите скорости автомобиля и мотоциклиста, если в 10 часов утра им оставалось до встречи 180 км.
Решение:
Совместно проехали $540 - 180 = 360$ км за $2$ часа
Скорость сближения: $360 : 2 = 180$ км/ч
Скорость автомобиля: $(180 - 20) : 2 = 80$ км/ч
Скорость мотоциклиста: $80 + 20 = 100$ км/ч
Ответ: 80 км/ч и 100 км/ч.
- Мастер на первую часть задания затратил 2 часа, а на вторую часть задания -3 часа. Всего за 5 часов он сделал 390 деталей. С какой производительностью работал мастер первые 2 часа, если его производительность в последние 3 часа была на 30 деталей в час больше, чем при выполнении первой части задания?
Решение:
Пусть производительность $x$ деталей/час
$2x + 3(x + 30) = 390$
$5x + 90 = 390$
$5x = 300$
$x = 60$
Ответ: 60 деталей/час.
- От квадратного листа фанеры, периметр которого 6 м, отпилили кусок шириной 10 дм. Найдите площадь и периметр оставшейся части.
Решение:
Сторона квадрата: $6 : 4 = 1,5$ м = $15$ дм
Оставшаяся ширина: $15 - 10 = 5$ дм
Периметр: $(15 + 5) \cdot 2 = 40$ дм
Площадь: $15 \cdot 5 = 75$ дм²
Ответ: 40 дм и 75 дм².
- Квадрат с площадью 81 дм² разрезали на четыре одинаковых квадрата, которые выложили в одну полосу. Найдите периметр этого прямоугольника.
Решение:
Сторона исходного квадрата: $9$ дм
Сторона маленького квадрата: $4,5$ дм
Периметр прямоугольника: $2 \cdot (4,5 \cdot 4 + 4,5) = 45$ дм
Ответ: 45 дм.
- Нина записала все числа от 1 до 110, включая 1 и 110. Сколько раз она написала цифру 1?
Решение:
Подсчёт единиц в разрядах:
Единицы: 11 раз (1, 11, 21, ..., 101)
Десятки: 11 раз (10-19, 110)
Сотни: 11 раз (100-110)
Всего: $11 + 11 + 10 = 33$
Ответ: 33.
- За один день работы гном может добыть 5, 7 или 11 драгоценных камней. Сможет ли гном за 9 дней работы добыть ровно 70 драгоценных камней?
Решение:
Сумма 9 нечётных чисел нечётна, 70 — чётное. Невозможно.
Ответ: Нет.
Материалы школы Юайти