Лицей №1514 из 4 в 5 класс 2010 год вариант 1

ГИМНАЗИЯ №1514

2010 год

Вариант 1

1. Выполни действия (все вычисления должны быть в чистовике):
   1. $125 \cdot 789 \cdot 8-987$;
   2. $(2203200: 108-8): 4+4902$.
2. Реши уравнения (проверку делать необязательно):
   1. $30 \cdot x-69=4731$;
   2. $64-(84: x+9)=27$.
3. Реши задачу (с пояснениями):
   1. На двух соседних сторонах прямоугольника построены два квадрата (как показано на рисунке). Периметр получившейся фигуры (фигура выделена жирной линией) равен 80 см. Найти площадь исходного прямоугольника, если его длина в 4 раза больше ширины.
      
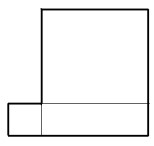
   2. Коля и Петя отправились на прогулку из деревни до опушки леса. Опушка находится в 12 километрах от деревни. Петя идёт со скоростью 2 км $/ ч$, а Коля - 4 км $/ ч$. Дойдя до опушки, Коля, не задерживаясь, с той же скоростью возвращается обратно. На каком расстоянии от деревни Коля встретит Петю?
4. Аня решала на доске пример на деление, но на перемене Игорь стёр с доски почти всё решение. Вот всё, что осталось:
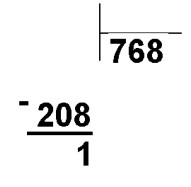   Помоги Ане восстановить всю запись.
5. Доктор Айболит раздал четырём заболевшим зверям 2010 чудодейственных таблеток. Носорог получил на одну больше, чем крокодил, бегемот на две больше, чем носорог, а слон - на 3 больше, чем бегемот. Сколько таблеток придётся съесть слону?

Решения задач

1. 1. Вычислить: $125 \cdot 789 \cdot 8 - 987$
      Решение:
      $125 \cdot 8 = 1000$
      $1000 \cdot 789 = 789\,000$
      $789\,000 - 987 = 788\,013$
      Ответ: $788\,013$.
      
      
   2. Вычислить: $(2\,203\,200 : 108 - 8) : 4 + 4\,902$
      Решение:
      $2\,203\,200 : 108 = 20\,400$
      $20\,400 - 8 = 20\,392$
      $20\,392 : 4 = 5\,098$
      $5\,098 + 4\,902 = 10\,000$
      Ответ: $10\,000.$
2. 1. Решить уравнение: $30 \cdot x - 69 = 4\,731$
      Решение:
      $30x = 4\,731 + 69 = 4\,800$
      $x = \frac{4\,800}{30} = 160$
      Ответ: 160.
      
      
   2. Решить уравнение: $64 - (84 : x + 9) = 27$
      Решение:
      $84 : x + 9 = 64 - 27 = 37$
      $84 : x = 37 - 9 = 28$
      $x = \frac{84}{28} = 3$
      Ответ: 3.
3. 1. Площадь прямоугольника.
      Решение:
      Пусть ширина прямоугольника $x$ см, тогда длина $4x$ см.
      Периметр фигуры равен сумме: $x + 4x + x + 4x + x + 4x = 15x$
      По условию $15x = 80 \Rightarrow x = \frac{80}{15} = 5\frac{1}{3}$ см
      Площадь прямоугольника: $x \cdot 4x = 4x^2 = 4 \cdot \left(\frac{16}{3}\right)^2 = \frac{1024}{9} \approx 113,78$ см²
      Ответ: $\frac{1024}{9}$ см².
      
      
   2. Встреча Коли и Пети.
      Решение:
      Время до встречи: $t$ часов.
      Путь Пети: $2t$ км.
      Путь Коли: $4t$ км (туда и обратно).
      Общий путь: $2t + 4t = 6t = 24$ км (двойное расстояние до опушки)
      $t = \frac{24}{6} = 4$ часа
      Расстояние от деревни: $2 \cdot 4 = 8$ км
      Ответ: 8 км.
4. Восстановление деления.
   Решение:
   Делимое: $\_\,90050$
   Делитель: $12$
   Частное: $7504$ (последняя цифра 4)
   Проверка: $12 \cdot 7504 = 90\,048$
   Остаток: $90\,050 - 90\,048 = 2$
   Ответ: $\phantom{0}90050 \div 12 = 7504$ (ост. 2).
   
   
5. Таблетки для слона.
   Решение:
   Пусть крокодил получил $x$ таблеток. Тогда:
   Носорог: $x + 1$
   Бегемот: $x + 3$
   Слон: $x + 6$
   Сумма: $x + (x + 1) + (x + 3) + (x + 6) = 4x + 10 = 2010$
   $4x = 2000 \Rightarrow x = 500$
   Слон получил: $500 + 6 = 506$ таблеток
   Ответ: 506.