8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1511 из 8 в 9 класс 2018 год вариант 4

Сложность:
Дата экзамена: 2018
Печать
youit.school ©

ЛИЦЕЙ №1511


2018 год


Вариант 4



Алгебра

  1. Вычислите:
    1. $0,7 \cdot \sqrt{1 \frac{15}{49}}+\frac{1}{5} \cdot \sqrt{0,0625} ;$
    2. $\sqrt{7+4 \sqrt{3}}+\sqrt{19-8 \sqrt{3}}$.
  2. Сократите дробь $\frac{6^{13}}{36^{5} \cdot 3^{3}}$.
  3. Каков знак числа $a$, если известно, что $12-3 a>15$ ?
  4. Решите систему неравенств: $\left\{\begin{array}{l}4 x-165\end{array}\right.$.
  5. Найдите корни уравнения: $\frac{3 x-5}{x+3}=\frac{3 x-1}{2+x}$.
  6. Решите уравнение $\frac{x}{x^{2}-2 x}-\frac{6}{4-x^{2}}=\frac{3}{x^{2}+2 x}$.
  7. Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 112 деталей, на 4 часа быстрее, чем второй рабочий, выполняюший такой же заказ. Сколько деталей в час делает второй рабочий?
  8. Упростите выражение $\frac{a^{2}+a b+b^{2}}{a^{3}+2 a^{2} b+a b^{2}}+\frac{(b-a)^{3}}{(a+b)^{2}} \cdot \frac{a}{(a-b)^{3}}-\frac{a}{a^{2}+a b}$.
  9. Постройте график функции $y=-x^{2}+5 x+6 .$ По графику определите:
    1) Область определения функции;
    2) Множество значений функции;
    3) Промежутки возрастания и убывания функции.

    Геометрия
  10. Укажите, какие тройки отрезков образуют прямоугольные треугольники, а какие нет, и докажите:
    1. $15 ; 39 ; 36 ;$
    2. $\frac{3}{4} ; 1 ; \frac{3}{5}$.
    3. $1 ; 1 \frac{2}{3} ; 1 \frac{1}{3}$.
  11. Высота равнобедренного треугольника равна половине боковой стороны. Найдите площадь треугольника, если его основание равно 6 дм.
  12. В параллелограмме $A B C D$ высоты $C H=6 \mathrm{~cm}, D P=10$ см. Периметр параллелограмма равен 48 см. Найдите площадь параллелограмма и его меньшую сторону.
  13. В прямоугольной трапеции $\mathrm{ABCK}$ большая боковая сторона равна $3 \sqrt{2}$, угол К равен $45^{\circ}$, а высота СН делит основание АК пополам. Найдите площадь трапеции.
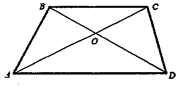
  14. Дано: $A B C D$ - трапеция, $S_{\triangle B O C}=3 \mathrm{~cm}^{2} ; S_{\triangle A O D}=27 \mathrm{~cm}^{2}$. Найдите:
    1) Отношение $B C$ к $A D$;
    2) Отношение периметров $\triangle A O D$ и $\triangle B O C$;
    3) Площадь $A B C D$.
  15. В четырехугольник $A B C D$ вписана окружность. $\mathrm{AB}=\mathrm{CD}, \mathrm{BC}=12$ см, периметр четырехугольника равен 54 см. Найдите длины всех сторон четырехугольника.
  16. Хорды $A B$ и $C D$ пересекаются в точке $M$. Найдите длину хорды $A B$, если $C M=4 \mathrm{~cm}, D M=9 \mathrm{~cm}, A M: M B=4 .$


Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите:
    1. $0,7 \cdot \sqrt{1 \frac{15}{49}} + \frac{1}{5} \cdot \sqrt{0,0625}$
      Решение:
      $\sqrt{1 \frac{15}{49}} = \sqrt{\frac{64}{49}} = \frac{8}{7}$
      $\sqrt{0,0625} = \sqrt{\frac{1}{16}} = \frac{1}{4}$
      $0,7 \cdot \frac{8}{7} = 0,8$, $\frac{1}{5} \cdot \frac{1}{4} = 0,05$
      $0,8 + 0,05 = 0,85$
      Ответ: 0,85.
    2. $\sqrt{7 + 4 \sqrt{3}} + \sqrt{19 - 8 \sqrt{3}}$
      Решение:
      Представим подкоренные выражения в виде квадратов:
      $\sqrt{(2 + \sqrt{3})^2} + \sqrt{(4 - \sqrt{3})^2} = |2 + \sqrt{3}| + |4 - \sqrt{3}| = 2 + \sqrt{3} + 4 - \sqrt{3} = 6$
      Ответ: 6.
  2. Сократите дробь $\frac{6^{13}}{36^{5} \cdot 3^{3}}$
    Решение:
    $36^5 = (6^2)^5 = 6^{10}$
    $\frac{6^{13}}{6^{10} \cdot 3^{3}} = \frac{6^{3}}{3^{3}} = \left(\frac{6}{3}\right)^3 = 2^3 = 8$
    Ответ: 8.
  3. Каков знак числа $a$, если $12 - 3a > 15$
    Решение:
    $12 - 3a > 15 \implies -3a > 3 \implies a < -1$
    Ответ: отрицательный.
  4. Решите систему неравенств: $\begin{cases} 4x - 16 5 \end{cases}$
    Решение:
    $4x < 16 \implies x < 4$
    $3x > 4 \implies x > \frac{4}{3}$
    Пересечение решений: $\frac{4}{3} < x < 4$
    Ответ: $(\frac{4}{3}; 4)$.
  5. Найдите корни уравнения: $\frac{3x - 5}{x + 3} = \frac{3x - 1}{2 + x}$
    Решение:
    $(3x - 5)(x + 2) = (3x - 1)(x + 3)$
    $3x^2 + 6x - 5x - 10 = 3x^2 + 9x - x - 3$
    $-10 = 3x + 3 \implies x = -\frac{13}{3}$
    Проверка ОДЗ: $x \neq -3, -2$
    Ответ: $-\frac{13}{3}$.
  6. Решите уравнение $\frac{x}{x^2 - 2x} - \frac{6}{4 - x^2} = \frac{3}{x^2 + 2x}$
    Решение:
    Приведем к общему знаменателю $x(x-2)(x+2)$:
    $x(x+2) - 6x = 3(x-2)$
    $x^2 + 2x - 6x - 3x + 6 = 0$
    $x^2 - 7x + 6 = 0 \implies x = 1$ или $x = 6$
    Проверка ОДЗ: $x \neq 0, 2, -2$
    Ответ: 1; 6.
  7. Производительность первого рабочего: $x + 9$ дет/ч, второго: $x$ дет/ч
    Составим уравнение:
    $\frac{112}{x} - \frac{112}{x + 9} = 4$
    $28(x + 9 - x) = x(x + 9)$
    $x^2 + 9x - 252 = 0 \implies x = 12$ (отрицательный корень отбрасываем)
    Ответ: 12 деталей в час.
  8. Упростите выражение:
    Разложим знаменатели на множители:
    $\frac{a^2 + ab + b^2}{a(a^2 + 2ab + b^2)} + \frac{-(a - b)^3}{(a + b)^2} \cdot \frac{a}{(a - b)^3} - \frac{a}{a(a + b)} = \frac{1}{a} - \frac{a}{a(a + b)} = \frac{1}{a} - \frac{1}{a + b}$
    Ответ: $\frac{1}{a} - \frac{1}{a + b} = \frac{b}{a(a + b)}$.
  9. График функции $y = -x^2 + 5x + 6$
    Вершина: $x = \frac{-b}{2a} = \frac{5}{2}$, $y = \frac{121}{4}$
    1) Область определения: $(-\infty; +\infty)$
    2) Множество значений: $(-\infty; \frac{121}{4}]$
    3) Возрастает на $(-\infty; \frac{5}{2}]$, убывает на $[\frac{5}{2}; +\infty)$
  10. Проверка на прямоугольные треугольники:
    1. $15^2 + 36^2 = 225 + 1296 = 1521 = 39^2$ – прямоугольный
    2. $\left(\frac{3}{4}\right)^2 + 1^2 ≠ \left(\frac{3}{5}\right)^2$ – нет
    3. $1^2 + (1\frac{1}{3})^2 = 1 + \frac{16}{9} = \frac{25}{9} = (1\frac{2}{3})^2$ – прямоугольный
  11. Высота $h = \frac{AB}{2}$, $AB = BC = x$
    По теореме Пифагора: $h^2 + (\frac{AC}{2})^2 = x^2$
    $\left(\frac{x}{2}\right)^2 + 9 = x^2 \implies x = 2\sqrt{3}$
    Площадь $S = \frac{1}{2} \cdot 6 \cdot \sqrt{3} = 3\sqrt{3}$ дм²
  12. Площадь параллелограмма: $6 \cdot b = 10 \cdot a$, периметр: $2(a + b) = 48$
    $a + b = 24$, из системы:
    $a = 9$, $b = 15$, площадь $S = 90$ см²
  13. Основание $AK = 2CH$, угол $45° \implies CK = 3\sqrt{2} \cdot \frac{\sqrt{2}}{2} = 3$
    Средняя линия: $\frac{AK + BC}{2} \cdot CH = \frac{6 + 3}{2} \cdot 3 = 13,5$
  14. Отношение $BC:AD = \sqrt{3:27} = 1:3$
    Отношение периметров $\sqrt{27:3} = 3:1$
    Площадь трапеции $S = 3 + 27 + 2\sqrt{3 \cdot 27} = 48$ см²
  15. Стороны $AB = CD$, сумма противоположных сторон $AB + BC = \frac{54}{2} = 27$ см
    $AB = CD = 15$ см, $BC = 12$ см, $AD = 54 - 15 - 12 - 15 = 12$ см
  16. По свойству пересекающихся хорд: $CM \cdot DM = AM \cdot MB$
    $4 \cdot 9 = 4x \cdot x \implies x = 3$, $AB = 4x + x = 15$ см
Материалы школы Юайти