Лицей №1511 из 8 в 9 класс 2018 год вариант 3
Печать
youit.school ©
ЛИЦЕЙ №1511
2018 год
Вариант 3
В задачах 1-11 надо записать только ответ
- На клетчатой бумаге с размером клетки $1 \times 1$ изображён угол. Найдите тангенс этого угла.
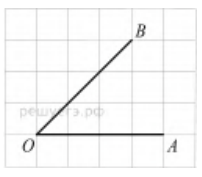
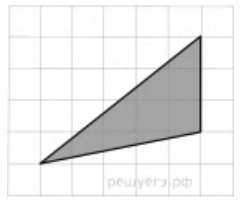
- Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см $\times 1$ см (см. рис сантиметрах. .). Ответ дайте в квадратных сантиметрах.
- В треугольнике $A B C$ угол $C$ равен $90^{\circ}, A C=4,8$, Найдите $A B .$
- В треугольнике $A B C$ угол $C$ равен 90 градусов, $B C=3, C H-$ высота $\quad$ Найдите $A H .$
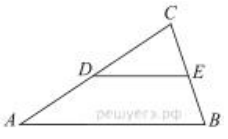
- Площадь треугольника $A B C$ равна 4. $D E$ - средняя линия. Найдите площадь треугольника CDE.
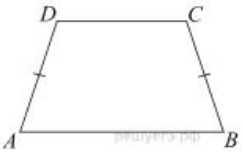
- Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
- Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна $10 .$ Найдите высоту, опущенную на вторую сторону параллелограмма.
- Найдите вписанный угол, опирающийся на дугу, которая составляет 5 окружности. Ответ дайте в градусах.
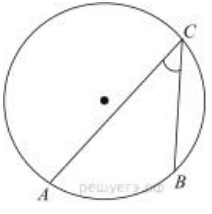
- Хорда $A B$ стягивает дугу окружности в $92^{\circ} .$ Найдите угол $A B C$ между этой хордой и касательной к окружности, проведенной через точку В. Ответ дайте в градусах.
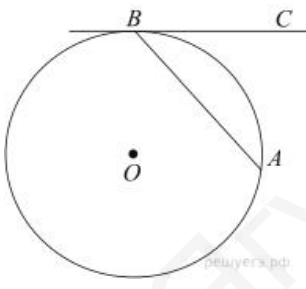
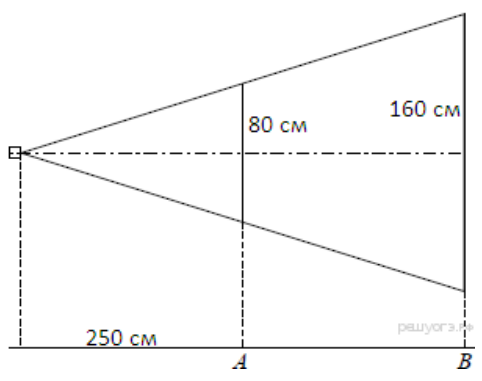
- Проектор полностью освещает экран $A$ высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран В высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
- Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.
3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.
4) Если вписанный угол равен $30^{\circ}$, то дуга окружности, на которую опирается этот угол, равна $60^{\circ}$.
Если утверждений несколько, запишите их номера в порядке возрастания.
К задачам 12-14 должно быть приведено полное решение. - В треугольнике $A B C$ с тупым углом $A C B$ проведены высоты $A A_{1}$ и $B B_{1}$. Докажите, что треугольники $A_{1} C B_{1}$ и $A C B$ подобны.
- Прямая, параллельная основаниям $M P$ и $N K$ трапеции $M N K P$, проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны $M N{ }_{\text {и }} K P$ в точках $A_{\text {и }} B$ соответственно. Найдите длину отрезка $A B$, если см, $N K=24 M P=40_{\text {см. }}$
- Длина катета $A C$ прямоугольного треугольника $A B C$ равна 3 см. Окружность с диаметром $A C$ пересекает гипотенузу $A B$ в точке $M$. Найдите площадь треугольника $A B C$, если известно, что $A M: M B=9: 16$
Материалы школы Юайти
youit.school ©
Решения задач
- На клетчатой бумаге с размером клетки $1 \times 1$ изображён угол. Найдите тангенс этого угла.
Решение: Угол образован горизонтальным катетом длиной 1 клетка и вертикальным катетом длиной 3 клетки. Тангенс угла равен отношению противолежащего катета к прилежащему: $\tan \alpha = \frac{3}{1} = 3$.
Ответ: 3.
- Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см $\times$ 1 см.
Решение: Треугольник прямоугольный с катетами 3 см и 4 см. Площадь равна $\frac{1}{2} \cdot 3 \cdot 4 = 6$ см$^2$.
Ответ: 6.
- В треугольнике $ABC$ угол $C$ равен $90^{\circ}$, $AC = 4,8$. Найдите $AB$.
Решение: По теореме Пифагора, если $BC = 6,4$, то $AB = \sqrt{AC^2 + BC^2} = \sqrt{4,8^2 + 6,4^2} = \sqrt{23,04 + 40,96} = \sqrt{64} = 8$.
Ответ: 8.
- В треугольнике $ABC$ угол $C$ равен $90^{\circ}$, $BC = 3$, $CH$ — высота. Найдите $AH$.
Решение: Высота $CH = \frac{AC \cdot BC}{AB} = \frac{4 \cdot 3}{5} = 2,4$. Тогда $AH = \frac{AC^2}{AB} = \frac{4^2}{5} = 3,2$.
Ответ: 3,2.
- Площадь треугольника $ABC$ равна 4. $DE$ — средняя линия. Найдите площадь треугольника $CDE$.
Решение: Средняя линия отсекает подобный треугольник с коэффициентом $\frac{1}{2}$. Площадь подобного треугольника в 4 раза меньше: $\frac{4}{4} = 1$.
Ответ: 1.
- Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Решение: Боковые стороны равны $\frac{60 - 14 - 26}{2} = 10$. Высота трапеции: $h = \sqrt{10^2 - 6^2} = 8$. Площадь: $\frac{14 + 26}{2} \cdot 8 = 160$.
Ответ: 160.
- Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону.
Решение: Площадь параллелограмма: $9 \cdot 10 = 90$. Высота на вторую сторону: $\frac{90}{15} = 6$.
Ответ: 6.
- Найдите вписанный угол, опирающийся на дугу, которая составляет $\frac{1}{5}$ окружности.
Решение: Вписанный угол равен половине дуги: $\frac{360^\circ}{5} \cdot \frac{1}{2} = 36^\circ$.
Ответ: 36.
- Хорда $AB$ стягивает дугу окружности в $92^\circ$. Найдите угол $ABC$ между этой хордой и касательной.
Решение: Угол между касательной и хордой равен половине дуги: $\frac{92^\circ}{2} = 46^\circ$.
Ответ: 46.
- Проектор полностью освещает экран высотой 80 см на расстоянии 250 см. Наименьшее расстояние для экрана 160 см:
Решение: Из подобия треугольников: $\frac{160}{80} = 2 \Rightarrow \frac{250}{2} = 125$ см.
Ответ: 125.
- Верные утверждения: 2, 3, 4.
Ответ: 234.
- В треугольнике $ABC$ с тупым углом $ACB$ проведены высоты $AA_1$ и $BB_1$. Докажите подобие треугольников $A_1CB_1$ и $ACB$.
Решение: Угол $C$ общий. Углы $A_1$ и $B_1$ прямые, как и углы при основании исходного треугольника. Следовательно, треугольники подобны по двум углам.
- Прямая, параллельная основаниям трапеции $MP = 40$ см и $NK = 24$ см, проходит через точку пересечения диагоналей. Длина отрезка $AB$:
Решение: Используя свойство средней гармонической: $AB = \frac{2 \cdot 40 \cdot 24}{40 + 24} = 30$ см.
Ответ: 30.
- Длина катета $AC$ прямоугольного треугольника $ABC$ равна 3 см. Окружность с диаметром $AC$ пересекает гипотенузу $AB$ в точке $M$. Площадь треугольника $ABC$:
Решение: Из соотношения $AM:MB = 9:16$ и свойства высоты: $AC^2 = AM \cdot AB \Rightarrow AB = 5$ см. Тогда $BC = 4$ см, площадь: $\frac{1}{2} \cdot 3 \cdot 4 = 6$ см$^2$.
Ответ: 6.
Материалы школы Юайти