Лицей №1511 из 8 в 9 класс 2018 год (вариант 2)

ЛИЦЕЙ №1511

2018 год

Вариант 2

1. Найдите значение выражения: $\left(\frac{14}{11}+\frac{17}{10}\right) \cdot \frac{11}{15}$
2. На каком из нижеперечисленных отрезков координатной прямой находится число $\sqrt{17}+2 ?$
   1) $[3 ; 4]$ 2) $[5 ; 6]$ 3) $[6 ; 7]$ 4) $[7 ; 8]$
3. Представьте выражение $\frac{\left(\mathrm{c}^{-3}\right)^{4}}{\mathrm{c}^{-17}}$ в виде степени с основанием $c$.
   1) $c^{18}$ 2) $\mathrm{c}^{5}$ 3) $\mathrm{c}^{-29}$ 4) $\mathrm{c}^{-16}$
4. Найдите корни уравнения $2 \mathrm{x}^{2}-11 \mathrm{x}-6=0$
5. Для каждого графика укажите соответствующую ему формулу.
   Графики
   
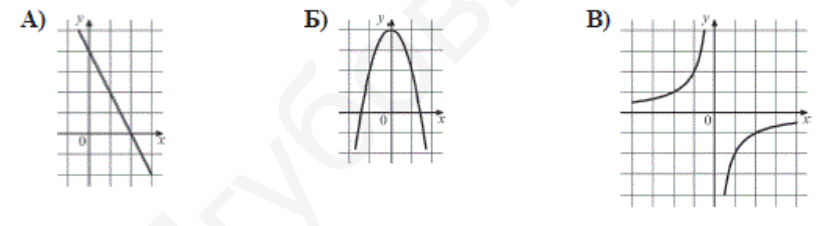
   1) $y=-2 x+4$ 2) $y=-\frac{2}{x}$ 3) $y=\sqrt{x}$ 4) $y=-2 x^{2}+4$
   

   $\mathrm{A}$	$\mathrm{B}$	$\mathrm{B}$

6. Николай старше Григория на 4 года, а Григорий старше Ильи в 1,5 раза. Вместе им 36 лет. Сколько лет Илье?
7. Упростите выражение $\frac{a^{2}-9 b^{2}}{2 a^{2}} \cdot \frac{a}{2 a+6 b}$ и найдите его значение при $a=\sqrt{2}$ и $b=\sqrt{50}$.
8. Решите неравенство $-5+2(7 x+2) \leq-8$. На каком рисунке изображено множество его решений?
9. Площадь заповедника была увеличена с 250 км $^{2}$ до 350 км $^{2} .$ На сколько процентов увеличилась площадь заповедника?
10. Какое из чисел больше: $\sqrt{7}+\sqrt{8}$ или $3+\sqrt{6} ?$
11. От пристани А к пристани В, расстояние между которыми равно 280 км. отправился с постоянной скоростью первый теплоход, а через 4 часа после этогоследом за ним со скоростью, на 8 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно

Решения задач

1. Найдите значение выражения: $\left(\frac{14}{11}+\frac{17}{10}\right) \cdot \frac{11}{15}$
   Решение:
   $\frac{14}{11} + \frac{17}{10} = \frac{140}{110} + \frac{187}{110} = \frac{327}{110}$
   $\frac{327}{110} \cdot \frac{11}{15} = \frac{327 \times 11}{110 \times 15} = \frac{327}{150} = \frac{109}{50} = 2,18$
   Ответ: 2,18
2. На каком из нижеперечисленных отрезков координатной прямой находится число $\sqrt{17}+2 ?$
   Решение: Оценим $\sqrt{17}$: $4^2 = 16 < 17 < 25 = 5^2$
   $\sqrt{17} \approx 4,12$, тогда $\sqrt{17} + 2 \approx 6,12 \in [6;7]$
   Ответ: 3
3. Представьте выражение $\frac{\left(\mathrm{c}^{-3}\right)^{4}}{\mathrm{c}^{-17}}$ в виде степени с основанием $c$.
   Решение: $\frac{c^{-12}}{c^{-17}} = c^{-12 - (-17)} = c^{5}$
   Ответ: 2
4. Найдите корни уравнения $2 \mathrm{x}^{2}-11 \mathrm{x}-6=0$
   Решение:
   $D = (-11)^2 - 4 \cdot 2 \cdot (-6) = 121 + 48 = 169$
   $x = \frac{11 \pm 13}{4} \Rightarrow x_1 = \frac{24}{4}=6,\; x_2 = \frac{-2}{4} = -0,5$
   Ответ: 6; -0,5
5. Для каждого графика укажите соответствующую ему формулу.
   Решение: - Графику A соответствует линейная функция с отрицательным угловым коэффициентом: $y = -2x + 4$ (1) - Графику B соответствует гипербола: $y = -\frac{2}{x}$ (2) - Графику В соответствует квадратичная функция с ветвями вниз: $y = -2x^2 +4$ (4)
   Ответ: 142
6. Николай старше Григория на 4 года, а Григорий старше Ильи в 1,5 раза. Вместе им 36 лет. Сколько лет Илье?
   Решение:
   Пусть Илье $x$ лет, тогда Григорий — $1,5x$, Николай — $1,5x + 4$.
   $x + 1,5x + (1,5x +4) = 36 \Rightarrow 4x +4 =36 \Rightarrow x=8$
   Ответ: 8
7. Упростите выражение $\frac{a^{2}-9 b^{2}}{2 a^{2}} \cdot \frac{a}{2 a+6 b}$ и найдите его значение при $a=\sqrt{2}$ и $b=\sqrt{50}$.
   Решение:
   $\frac{(a-3b)(a+3b)}{2a^2} \cdot \frac{a}{2(a + 3b)} = \frac{a -3b}{4a}$
   Подставим значения: $a -3b = \sqrt{2} - 3\sqrt{50} = \sqrt{2} -15\sqrt{2} = -14\sqrt{2}$
   $\frac{-14\sqrt{2}}{4\sqrt{2}} = -3,5$
   Ответ: -3,5
8. Решите неравенство $-5+2(7 x+2) \leq-8$.
   Решение:
   $-5 +14x +4 \leq -8 \Rightarrow 14x \leq -7 \Rightarrow x \leq -0,5$
   Ответ: 4
9. Площадь заповедника была увеличена с 250 км$^{2}$ до 350 км$^{2}$. Увеличение на $100$ км$^{2}$.
   $\frac{100}{250} \times 100% = 40\%$
   Ответ: 40
10. Какое из чисел больше: $\sqrt{7}+\sqrt{8}$ или $3+\sqrt{6}$?
    Решение: Возведём в квадрат:
    $(\sqrt{7}+\sqrt{8})^2 =7 +8 +2\sqrt{56} \approx29,97$ \quad $(3+\sqrt{6})^2=15 +6\sqrt{6}\approx29,7$
    Ответ: $\sqrt{7}+\sqrt{8} > 3+\sqrt{6}$
11. Пусть скорость первого теплохода $x$ км/ч. Время пути первого: $\frac{280}{x}$, второго: $\frac{280}{x+8}$. Разница во времени 4 часа:
    $\frac{280}{x} - \frac{280}{x+8} =4$
    Решение уравнения: $4x(x+8)=280 \cdot8$
    $x^2 +8x -560 =0$. Корень: $x=20$
    Ответ: 20