8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1511 из 7 в 8 класс 2018 год (вариант 2)

Сложность:
Дата экзамена: 2018
Сложность:
Дата экзамена: 2018
youit.school ©

ЛИЦЕЙ №1511


2018 год


Вариант 2 - 180 минут



  1. В следующих заданиях запишите ответ.
    Найдите значение выражения $(\sqrt{23}+1)^{2} .$ В ответе укажите номер правильного варианта.
    1. $22+2 \sqrt{23}$
    2. 22
    3. $24+2 \sqrt{23}$
    4. $24+\sqrt{23}$
  2. Решите уравнение $x^{2}=2 x+8$. Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
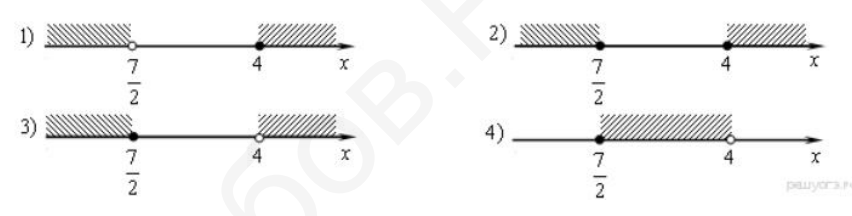
  3. На каком рисунке изображено множество решений неравенства $\frac{2 x-7}{4-x} \geq 0$ В ответе укажите номер правильного варианта.
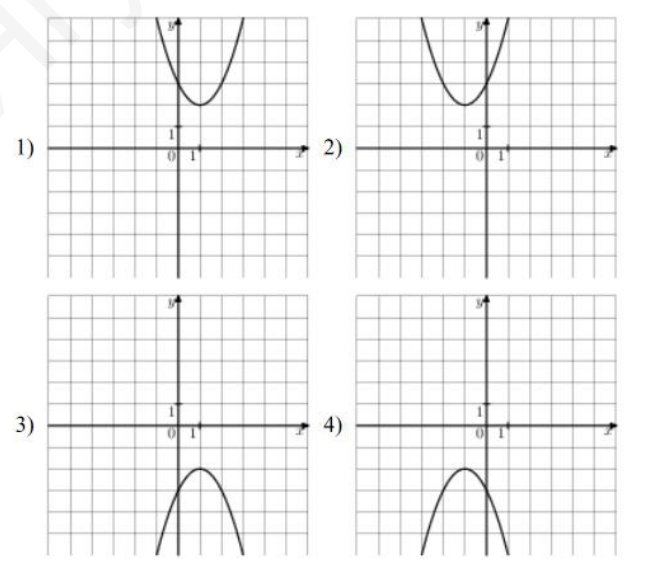
  4. На одном из рисунков изображен график функции $y=x^{2}-2 x+3 .$ Укажите номер этого рисунка.
  5. Найдите значение выражения $\left(\frac{a+2 b}{a^{2}-2 a b}-\frac{1}{a}\right): \frac{b}{2 b-a}$ при $a=1,6, b=\sqrt{2}-1 .$
  6. Квадратный трёхчлен разложен на множители: $2 x^{2}-13 x+15=2(x-5)(x-a) .$ Найдите $a .$
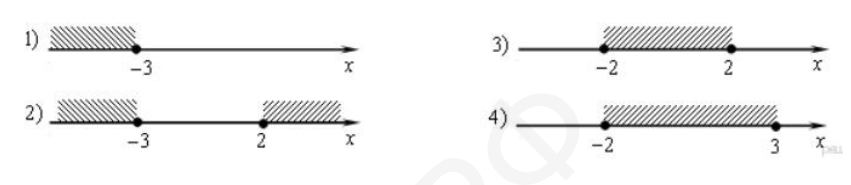
  7. Решите систему неравенств $\left\{\begin{array}{l}x^{2} \leq 4, \\ x+3 \geq 0 .\end{array}\right.$
    На каком из рисунков изображено множество её решений?
    В ответе укажите номер правильного варианта.
    II часть. В следующих заданиях запишите полное обоснованное решение и ответ.
  8. Вычислите: $\sqrt{9-4 \sqrt{2}}-\frac{7}{2 \sqrt{2}+1}$.
  9. Решите уравнение:
    1. $\frac{3}{x^{2}+9 x+18}=\frac{2 x+7}{6-5 x-x^{2}}+\frac{1}{x+3}$;
    2. $\frac{21}{x^{2}-4 x+10}+4 x=x^{2}+6$
  10. Решите неравенство:
    1. $\frac{7}{2 x-1} \geq 6$
    2. $\left|x^{2}+3 x\right|<x+4$
  11. Из пункта $A$ в пункт $B$, расстояние между которыми равно 60 км, выехал автобус, а через 20 мин. вслед за ним выехал легковой автомобиль, скорость которого на 20 км/ч больше скорости автобуса. Автобус пришел в пункт $B$ на 10 мин. позже легкового автомобиля. Найдите скорости автобуса и легкового автомобиля.
    1. Постройте график функции $f(x)=x^{2}-6|x|+5$.
    2. При каких значениях параметра $a$ уравнение $f(x)=a$ имеет ровно два решения?
    3. Укажите промежутки возрастания и убывания функции.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Правильный ответ: $(\sqrt{23}+1)^2 = 23 + 2\sqrt{23} + 1 = 24 + 2\sqrt{23}$
    Ответ: в.
  2. Решение уравнения $x^2 = 2x + 8$:
    $x^2 - 2x - 8 = 0$
    Дискриминант $D = 4 + 32 = 36$
    Корни: $x = \frac{2 \pm 6}{2} \Rightarrow x_1 = 4$, $x_2 = -2$
    Ответ: -24.
  3. Неравенство $\frac{2x - 7}{4 - x} \geq 0$. Нули числителя: $x = 3{,}5$. Знаменатель обращается в 0 при $x = 4$. Метод интервалов:
    Интервалы: $(-\infty, 3{,}5)$, $(3{,}5, 4)$, $(4, +\infty)$
    Решение: $x \in [3{,}5; 4)$
    Ответ: 2.
  4. Парабола $y = x^2 - 2x + 3 = (x-1)^2 + 2$. Вершина в точке $(1; 2)$, ветви вверх.
    Ответ: 3.
  5. Упрощение выражения: \[ \left(\frac{a+2b}{a^2 - 2ab} - \frac{1}{a}\right) : \frac{b}{2b - a} = \frac{4b}{a(a - 2b)} \cdot \frac{2b - a}{b} = -\frac{4}{a} \] Подставляем $a = 1{,}6$:
    $-\frac{4}{1{,}6} = -2{,}5$
    Ответ: -2,5.
  6. Разложение квадратного трёхчлена: \[ 2x^2 - 13x + 15 = 2(x - 5)\left(x - \frac{3}{2}\right) \Rightarrow a = \frac{3}{2} \] Ответ: 1,5.
  7. Система неравенств: \[ \begin{cases} x^2 \leq 4 \\ x + 3 \geq 0 \end{cases} \Rightarrow x \in [-2, 2] \] Ответ: 1.
  8. Вычисление $\sqrt{9 - 4\sqrt{2}} - \frac{7}{2\sqrt{2} + 1}$:
    $\sqrt{9 - 4\sqrt{2}} = 2\sqrt{2} - 1$
    $\frac{7}{2\sqrt{2} + 1} = 2\sqrt{2} - 1$
    Результат: $0$
    Ответ: 0.
  9. Решение уравнений:
    1. \[ \frac{3}{(x+3)(x+6)} = \frac{2x + 7}{(6 - x)(x + 1)} + \frac{1}{x + 3} \] Общий знаменатель: $(x+3)(x+6)(x-1)$. После преобразований:
      $x +8=0 \Rightarrow x = -8$
      Ответ: -8.
    2. \[ \frac{21}{x^2 - 4x + 10} + 4x = x^2 + 6 \Rightarrow x^2 -4x = t \] Решение: $t=7 \Rightarrow x=1$, $x=3$
      Ответ: 1;3.
  10. Решение неравенств:
    1. \[ \frac{7}{2x - 1} \geq 6 \Rightarrow x \in \left(\frac{1}{2}; \frac{13}{12}\right] \] Ответ: $\left(\frac{1}{2}; \frac{13}{12}\right]$.
    2. \[ |x^2 + 3x| < x + 4 \Rightarrow x \in (-1 - \sqrt{5}; -1 + \sqrt{5}) \] Ответ: ($-1$ - $\sqrt{5}$; $-1$ + $\sqrt{5}$).
  11. Автобус и автомобиль:
    Уравнение времени: \[ \frac{60}{x} = \frac{60}{x + 20} + \frac{1}{2} \] Решение: $x=40$ км/ч (автобус), $x+20=60$ км/ч (автомобиль)
    Ответ: 40 км/ч и 60 км/ч.
  12. График функции $f(x) = x^2 - 6|x| + 5$:
    1. График строится из двух парабол с вершинами в $(\pm3,-4)$.
    2. Уравнение $f(x)=a$ имеет 2 решения при $a=-4$ или $a>5$.
      Ответ: a=-4 или a>5.
    3. Функция убывает на $(-\infty,-3)$ и $(0,3)$; возрастает на $(-3,0)$ и $(3,+\infty)$.
Материалы школы Юайти