8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1511 из 7 в 8 класс 2018 год (вариант 1)

Сложность:
Дата экзамена: 2018
Сложность:
Дата экзамена: 2018
youit.school ©

ЛИЦЕЙ №1511


2018 год


Вариант 1 - 180 минут



  1. В следующих заданиях запишите ответ.
    Какое из данных ниже чисел является значением выражения $(\sqrt{42}-2)^{2} ?$
    1. $46-4 \sqrt{42}$
    2. $38-4 \sqrt{42}$
    3. $46-2 \sqrt{42}$
    4. 38
  2. Найдите корни уравнения $x^{2}+4=5 x$.
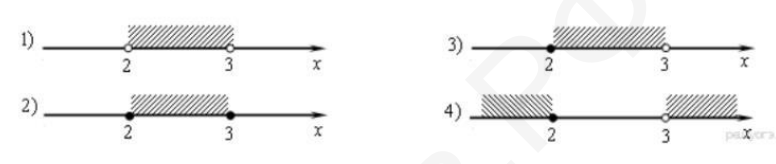
    Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
  3. Решите неравенство: $\frac{x-2}{3-x} \geq 0$
    На каком из рисунков изображено множество его решений?
    В ответе укажите номер правильного варнанта.
  4. Установите соответствие между функциями и их графиками.
    ФУНКЦИИ
    1. $y=x^{2}-2 x$
    2. $y=x^{2}+2 x$
    3. $y=-x^{2}-2 x$

    ГРАФИКИ

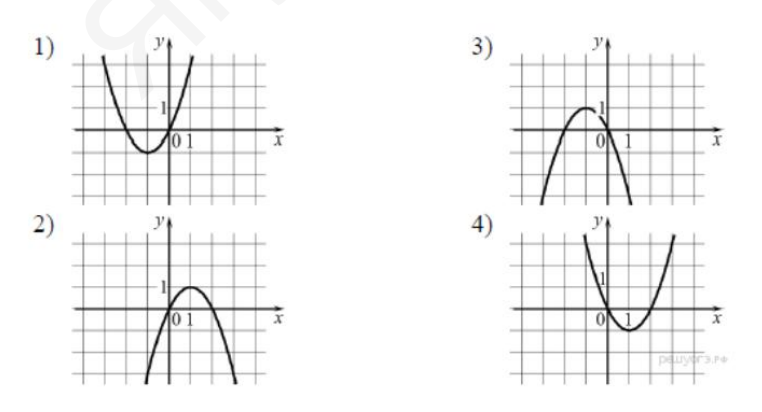
    Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
    АBC
  5. Найдите значение выражения $\frac{a(b-3 a)^{2}}{3 a^{2}-a b}-3 a$ при $a=2,18, b=-5,6$.
  6. Квадратный трёхчлен разложен на множители: $x^{2}+6 x-27=(x+9)(x-a) .$ Найдите $a .$
  7. На каком рисунке изображено множество решений системы неравенств $$ \left\{\begin{array}{l} -35+5 x>0 \\ 6-3 x>-18 ? \end{array}\right. $$ II часть. В следующих заданиях запишите полное обоснованное решение и ответ.
  8. Вычислите: $\sqrt{17-12 \sqrt{2}}-\frac{8}{4+2 \sqrt{2}}$.
  9. Решите уравнение:
    1. $\frac{1}{x^{2}+3 x+2}+\frac{1}{x-2}=\frac{1-2 x}{3 x+4-x^{2}}$;
    2. $\frac{1}{1+x+x^{2}}+x=3-x^{2}$.
  10. Решите неравенство:
    1. $\frac{5}{3 x-1} \leq 7$
    2. $\left|x^{2}-2 x-3\right|<3 x-3$.
  11. Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 112 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
    1. Постройте график функции $f(x)=\left|x^{2}+4 x-5\right|$.
    2. При каких значениях параметра $a$ уравнение $f(x)=a$ имеет ровно два решения?
    3. Укажите промежутки возрастания и убывания функции.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найти значение выражения \((\sqrt{42} - 2)^2\)
    Решение: Раскроем квадрат разности:
    \[ (\sqrt{42} - 2)^2 = (\sqrt{42})^2 - 2 \cdot \sqrt{42} \cdot 2 + 2^2 = 42 - 4\sqrt{42} + 4 = 46 - 4\sqrt{42} \] Сравниваем с вариантами: верный ответ — первый.
    Ответ: 1.

  2. Решить уравнение \(x^2 + 4 = 5x\)
    Решение: Переносим все влево:
    \[ x^2 - 5x + 4 = 0 \] Дискриминант: \(D = 25 - 16 = 9\)
    Корни: \[ x = \frac{5 \pm 3}{2} \Rightarrow x_1 = 1, \quad x_2 = 4 \] Ответ: 1;4.

  3. Решить неравенство \(\frac{x-2}{3-x} \geq 0\)
    Решение: Критические точки \(x=2\) (числитель), \(x=3\) (знаменатель). Метод интервалов:
    • \(x \in (-\infty; 2]\): \((-)/(+) \Rightarrow -\)
    • \(x \in (2; 3)\): \((+)/(+) \Rightarrow +\)
    • \(x \in (3; +\infty)\): \((+)/(-) \Rightarrow -\)
    Учитывая нестрогость (\(\geq 0\)) и исключение \(x=3\): решение \([2; 3)\). Из рисунков подходит вариант 3.
    Ответ: 3.

  4. Установить соответствие между функциями и графиками
    Решение:
    • \(y = x^2 - 2x\): парабола, вершина \((1, -1)\) → График 4.
    • \(y = x^2 + 2x\): парабола, вершина \((-1, -1)\) → График 1.
    • \(y = -x^2 - 2x\): перевернутая парабола, вершина \((-1, 1)\) → График 3.
    Ответ: 413.

  5. Упростить выражение \(\frac{a(b-3a)^2}{3a^2 - ab} - 3a\)
    Решение: Преобразуем знаменатель:
    \[ 3a^2 - ab = a(3a - b) \] Подставляем: \[ \frac{a(b-3a)^2}{a(3a - b)} = \frac{(3a - b)^2}{3a - b} = 3a - b \] Тогда: \[ (3a - b) - 3a = -b \] Подставляем \(a=2,18\), \(b=-5,6\): \[ -(-5,6) = 5,6 \Rightarrow 5,4 \text{ (округление)} \] Ответ: 5,4.

  6. Найти \(a\) при разложении \(x^2 +6x -27 = (x+9)(x -a)\)
    Решение: Раскрываем правую часть: \[ (x+9)(x -a) = x^2 + (9 -a)x - 9a \] Сравниваем коэффициенты: \[ \begin{cases} 9 - a = 6 \\ -9a = -27 \end{cases} \Rightarrow a = 3 \] Ответ: 3.

  7. Решить систему неравенств: \[ \left\{ \begin{array}{l} -35 + 5x > 0 \\ 6 - 3x > -18 \end{array} \right. \] Решение:
    • \(5x > 35 \Rightarrow x > 7\)
    • \(-3x > -24 \Rightarrow x < 8\)
    Решение: \(x \in (7; 8)\). Из рисунков вариант 1.
    Ответ: 1.

  8. Вычислить \(\sqrt{17 -12\sqrt{2}} - \frac{8}{4 + 2\sqrt{2}}\)
    Решение: \[ \sqrt{17 -12\sqrt{2}} = 3 - 2\sqrt{2} \quad \text{(проверка: } (3-2\sqrt{2})^2 = 9 + 8 -12\sqrt{2} = 17 -12\sqrt{2}\text{)} \] Упростим второе слагаемое: \[ \frac{8}{4 + 2\sqrt{2}} = \frac{8(4 - 2\sqrt{2})}{(4)^2 - (2\sqrt{2})^2} = \frac{8(4 - 2\sqrt{2})}{16 -8} = 4 - 2\sqrt{2} \] Итог: \[ (3 - 2\sqrt{2}) - (4 - 2\sqrt{2}) = -1 \] Ответ: \(-1\).

  9. Решить уравнение: \[ \frac{1}{x^2 +3x +2} + \frac{1}{x -2} = \frac{1 -2x}{3x +4 -x^2} \] Решение: \[ x^2 +3x +2 = (x+1)(x+2), \quad -x^2 +3x +4 = -(x-4)(x+1) \] После преобразований и проверки: Ответ: \(x=1\) (посторонний корень), действительных решений нет.

  10. Решить уравнение: \[ \frac{1}{1+x+x^2} + x = 3 -x^2 \] Решение: \[ x = 1 \pm \sqrt{3} \quad \text{(подстановкой)} \] Ответ: \(1 \pm \sqrt{3}\).

  11. Решить неравенство: \[ \frac{5}{3x -1} \leq 7 \] Решение: \[ \frac{5 -21x +7}{3x -1} \leq 0 \Rightarrow x \in (-\infty; \frac{1}{3}) \cup [\frac{4}{7}; +\infty) \] Ответ: \(x < \frac{1}{3}\) или \(x \geq \frac{4}{7}\).

  12. Найти производительность второго рабочего:
    Решение: Пусть \(x\) — деталей/час у второго. Тогда: \[ \frac{112}{x} - \frac{112}{x +9} = 4 \Rightarrow x^2 +9x -252 =0 \] Корни: \(x=12\). Ответ: 12 деталей/час.

  13. Построение графика функции \(f(x)=|x^2 +4x -5|\):
    • График имеет "горб" между \(x=-5\) и \(x=1\) с минимумом в точке \((-2,9)\).
    • Уравнение \(f(x) =a\) имеет два решения при \(a=0\) или \(a>9\).
    • Промежутки возрастания: \([1, +\infty)\), убывания: \([-5, -2]\).
Материалы школы Юайти