Лицей №1511 из 7 в 8 класс 2017 год (вариант 2)

ЛИЦЕЙ №1511

2017 год

Вариант 2

1. Вычислите: $\left(4 \sqrt{8}+\frac{1}{2} \sqrt{32}-\frac{1}{3} \sqrt{18}\right) \cdot \sqrt{2}$. Ответ:
2. Упростите выражение: $10 a-5(1+a)^{2}$. Ответ:
3. Из уравнения прямой $y=k x+b$ выразите угловой коэффициент $k$. Ответ:
4. В треугольнике $A B C$ угол $A=40^{\circ}$, угол $C=50^{\circ} .$ Найти угол между высотой $B H$ и биссектрисой $B D .$ Ответ:
5. Выполните деление дробей $\frac{9 x^{2}-6 x+1}{x^{2}-1}: \frac{3 x-1}{x+1} .$ Ответ:
6. Решите систему уравнений: $\left\{\begin{array}{l}2 x+5 y=4, \\ 3 x+10 y=8 .\end{array}\right.$ Ответ:
7. Решите неравенство: $5(x+2)-6 x<8 x-8$. Ответ:
8. Не решая уравнение, определите, сколько оно имеет корней. Соотнесите уравнения с ответами.
   1) $x^{2}+8 x+16=0$.
   2) $2 x^{2}+3 x-5=0$.
   3) $x^{2}-7 x+18=0$.
   А) Два корня.
   Б) Один корень.
   В) Нет действительных корней.
   Ответ:
   

   $\mathrm{A}$	Б	$\mathrm{B}$

9. Расстояние между пристанями катер проходит по течению реки за 2 часа, а против течения реки за 3 часа. Какова скорость течения реки, если скорость катера в стоячей воде $25 \mathrm{~km} /$ч?
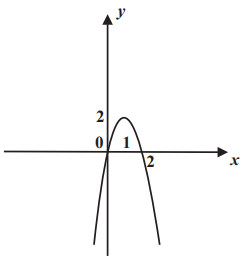
10. По графику квадратичной функции найдите, при каких значениях $x$ значения функции положительны.
    
    Часть В
    Привести полное решение и ответ
    В1. Найдите сумму корней уравнения: $25 x^{2}-9=0$.
    В2. Найдите значение выражения $(3 x-2)^{2}-(3 x+2)^{2}$ при $x=-\frac{1}{24}$.
    В3. При помоле пшеницы получается $80 \%$ муки. Сколько пшеницы нужно смолоть, чтобы получить 220 кг пшеничной муки?
    В4. В ромбе $A B C D$ диагональ $A C=4 \sqrt{5}$, а радиус вписанной окружности $4 .$ Найти площадь ромба.
    В5. Известно, что график функции $y=b x^{2}-5 x+5$ проходит через точку $D(1 ; 3) .$ Найдите абсциссу вершины параболы.