Школа №1502 из 9 в 10 класс 2021 год вариант 1

ШКОЛА №1502

2021 год

Вариант 1

1. Упростите выражение \[ \sin^2\bigl(180^\circ + 3\alpha\bigr)\,\frac{\sin(3\alpha - 90^\circ)}{\sin(360^\circ - 3\alpha)}\;\ctg(180^\circ - 3\alpha). \]
2. Вычислите \[ 0{,}1\cdot\sqrt{20} : \sqrt{45} - 2\frac{17}{30}. \]
3. Найдите производную функции \[ y = \sqrt{x}\cos x. \]
4. Найдите производную функции \[ y = \Bigl(-2\tg\frac{x}{4} - \frac{2}{^4\sqrt{x}}\Bigr)^{6}. \]
5. Найдите тангенс угла наклона касательной, проведённой к графику функции \[ f(x) = x - 2\sqrt{x} \] в его точке с абсциссой \(x_0 = 4\).
6. Решите неравенство \[ \sqrt{14 - x} \;\ge\; -5. \]
7. На рисунке изображён график производной функции \(f(x)\), определённой на интервале \((-10;8)\). Найдите количество точек экстремума функции \(f(x)\) на отрезке \([-4;8]\).
   

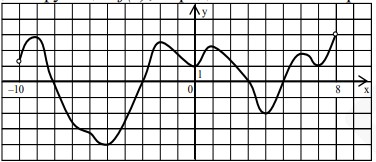
Часть 2. Ответом на каждое задание № 8–13 должно быть некоторое целое число или число, записанное в виде десятичной дроби. Это число надо записать в бланк ответов.

1. Укажите количество целых решений неравенства \[ \frac{4 - x}{x - 5} \;\ge\; \frac{1}{1 - x}. \]
2. Найдите значение выражения \[ -\frac{18x_0}{\pi}, \] где \(x_0\) — наименьший положительный корень уравнения \(\sin^2 x + 2\sin x = 0\).
3. Решите уравнение \[ \frac{\sqrt{22x - 13} - 5x + 2}{\sqrt{x + 24} - 5} = 0. \]
4. Дано \(\tg\alpha = -\tfrac{4}{3}\), \(\tfrac{\pi}{2} < \alpha < \pi\). Найдите \(\cos 2\alpha\).
5. Найдите сумму наибольшего и наименьшего значений функции \[ f(x) = 2x^3 + 9x^2 - 24x + 1 \] на отрезке \([-2;2]\).
6. Пусть \(x_0\) — точка минимума функции \[ f(x) = 5 - \sqrt[3]{\,(x^2 - 1)^2}\!. \] Найдите \(f(x_0)\).
7. Вычислите \[ \cos\!\bigl(\arctg(-\tfrac{1}{4})\bigr). \]
8. Два тела совершают прямолинейное движение по законам \[ s_1(t)=3t^2-2t+10,\quad s_2(t)=t^2+5t+1, \] где \(s\)—путь в метрах, \(t\)—время в секундах. Через сколько секунд, считая от \(t=0\), скорость движения первого тела будет в два раза больше скорости второго тела?

Часть 3. Запишите номер задания, а затем его полное решение

1. a) Решите уравнение \[ 6\cos^2\!\Bigl(\tfrac{3\pi}{2}-x\Bigr) +\sin2x\cdot\cos\!\Bigl(\tfrac{7\pi}{3}\Bigr) =2+\cos^2x. \]
2. б) Найдите корни на отрезке \(\bigl[-\tfrac{9\pi}{2};\,-3\pi\bigr]\).
3. Найдите все корни уравнения \[ \sin^2x+\sin^2 2x+\sin^2 3x+\sin^2 4x =-2\sin\!\Bigl(-\tfrac{17\pi}{4}\Bigr)\cos\!\Bigl(-\tfrac{9\pi}{4}\Bigr), \] принадлежащие области определения функции \(\;y=\sqrt{\pi^2-4x^2}.\)
4. Решите неравенство \[ \sqrt{9x-20}\;<\;x. \]
5. Решите уравнение \[ \sqrt{3x-2\sqrt{3x-1}} \;=\; 1-\sqrt{3x-4\sqrt{3x-1}+3}. \]
6. (10–в, г, е, ж, и, к, л, м, н) Исследуйте свойства функции и постройте график \[ y=\frac{\bigl(\sqrt{x+2}^{\;2}-3\bigr)(x+1)(4-x^3)}{x^4-x^2}. \]
7. (10–в, г, д, е, ж, з, и, к, л, м, н) Решите неравенство \[ \frac{4-3x}{2x-1} +11\sqrt{\frac{3x-4}{2x-1}} >24. \]
8. (10–д, з) Исследуйте свойства функции и постройте график \[ y=\sqrt[3]{x^3-x}. \]

Решения задач

1. Упростите выражение \[ \sin^2\bigl(180^\circ + 3\alpha\bigr)\,\frac{\sin(3\alpha - 90^\circ)}{\sin(360^\circ - 3\alpha)}\;\ctg(180^\circ - 3\alpha). \] Решение: Преобразуем тригонометрические функции с помощью формул приведения: \[ \sin(180^\circ + 3\alpha) = -\sin3\alpha, \quad \sin^2(180^\circ + 3\alpha) = \sin^23\alpha; \] \[ \sin(3\alpha - 90^\circ) = -\cos3\alpha, \quad \sin(360^\circ - 3\alpha) = -\sin3\alpha; \] \[ \ctg(180^\circ - 3\alpha) = -\ctg3\alpha. \] Подставляем в исходное выражение: \[ \sin^23\alpha \cdot \frac{-\cos3\alpha}{-\sin3\alpha} \cdot (-\ctg3\alpha) = \sin^23\alpha \cdot \frac{\cos3\alpha}{\sin3\alpha} \cdot (-\ctg3\alpha) = -\cos^23\alpha. \] Ответ: \( -\cos^2 3\alpha \).
2. Вычислите \[ 0{,}1\cdot\sqrt{20} : \sqrt{45} - 2\frac{17}{30}. \] Решение: \[ \sqrt{20} = 2\sqrt{5}, \quad \sqrt{45} = 3\sqrt{5}; \] \[ 0{,}1 \cdot \frac{2\sqrt{5}}{3\sqrt{5}} = \frac{0{,}2}{3} = \frac{1}{15}; \] \[ 2\frac{17}{30} = \frac{77}{30}; \] \[ \frac{1}{15} - \frac{77}{30} = -\frac{75}{30} = -2{,}5. \] Ответ: \(-2{,}5\).
3. Найдите производную функции \[ y = \sqrt{x}\cos x. \] Решение: Применяем правило производной произведения: \[ y' = \left(\sqrt{x}\right)' \cos x + \sqrt{x} \cdot (\cos x)' = \frac{\cos x}{2\sqrt{x}} - \sqrt{x} \sin x. \] Ответ: \( \frac{\cos x}{2\sqrt{x}} - \sqrt{x}\sin x \).
4. Найдите производную функции \[ y = \Bigl(-2\tg\frac{x}{4} - \frac{2}{\sqrt[4]{x}}\Bigr)^{6}. \] Решение: Используем цепное правило и производные элементарных функций: \[ u = -2\tg\frac{x}{4} - \frac{2}{x^{1/4}}, \quad y = u^6; \] \[ u' = -2 \cdot \frac{1}{4}\sec^2\frac{x}{4} + \frac{1}{2x^{5/4}}; \] \[ y' = 6u^5 \cdot \left(-\frac{1}{2}\sec^2\frac{x}{4} + \frac{1}{2x^{5/4}}\right). \] Ответ: \( 3\left(-2\tg\frac{x}{4} - \frac{2}{\sqrt[4]{x}}\right)^5 \left(\frac{1}{x^{5/4}} - \sec^2\frac{x}{4}\right) \).
5. Найдите тангенс угла наклона касательной к графику функции \( f(x) = x - 2\sqrt{x} \) в точке \( x_0 = 4 \). Решение: \[ f'(x) = 1 - \frac{1}{\sqrt{x}}, \quad f'(4) = 1 - \frac{1}{2} = 0{,}5. \] Ответ: \( 0{,}5 \).
6. Решите неравенство \[ \sqrt{14 - x} \ge -5. \] Решение: Левая часть всегда неотрицательна, неравенство выполняется для всех \( x \leq 14 \). Ответ: \( x \in (-\infty; 14] \).
7. Найдите количество точек экстремума функции \( f(x) \) на отрезке \([-4;8]\) по графику производной.
   Ответ: 3.
8. Количество целых решений неравенства \[ \frac{4 - x}{x - 5} \ge \frac{1}{1 - x}. \] Решение: Преобразуем неравенство и решаем методом интервалов. Целые решения: \( x = 2, 3, 4 \). Ответ: 3.
9. Найдите \(-\frac{18x_0}{\pi}\), где \(x_0\) — наименьший положительный корень уравнения \(\sin^2 x + 2\sin x = 0\). Решение: Корни уравнения \( x = \pi k \). Наименьший положительный корень \( x_0 = \pi \). \[ -\frac{18 \cdot \pi}{\pi} = -18. \] Ответ: \(-18\).
10. Решите уравнение \[ \frac{\sqrt{22x - 13} - 5x + 2}{\sqrt{x + 24} - 5} = 0. \] Решение: Числитель равен нулю при \( x = \frac{17}{25} = 0{,}68 \). Знаменатель не равен нулю. Ответ: \( 0{,}68 \).
11. Найдите \(\cos 2\alpha\) при \(\tg\alpha = -\tfrac{4}{3}\), \(\tfrac{\pi}{2} < \alpha < \pi\). Решение: \[ \cos2\alpha = \frac{1 - \tan^2\alpha}{1 + \tan^2\alpha} = \frac{1 - \frac{16}{9}}{1 + \frac{16}{9}} = -\frac{7}{25} = -0{,}28. \] Ответ: \(-0{,}28\).
12. Найдите сумму наибольшего и наименьшего значений функции \( f(x) = 2x^3 + 9x^2 - 24x + 1 \) на отрезке \([-2;2]\). Решение: Значения функции в точках \( x = -2, 1, 2 \): \[ f(-2) = 69, \quad f(1) = -12, \quad f(2) = 5. \] Сумма: \( 69 + (-12) = 57 \). Ответ: 57.
13. Найдите \( f(x_0) \), где \(x_0\) — точка минимума функции \( f(x) = 5 - \sqrt[3]{(x^2 - 1)^2} \). Решение: Производная равна нулю при \( x = 0 \). Значение функции: \( f(0) = 4 \). Ответ: 4.
14. Вычислите \(\cos(\arctg(-\tfrac{1}{4}))\). Решение: \[ \cos\theta = \frac{4}{\sqrt{17}}, \quad \text{где } \theta = \arctg(-\tfrac{1}{4}). \] Ответ: \( \frac{4\sqrt{17}}{17} \).
15. Время, когда скорость первого тела в два раза больше скорости второго: Решение: Решаем уравнение \( 6t - 2 = 2(2t + 5) \Rightarrow t = 6 \). Ответ: 6.