Лицей №146 из 7 в 8 класс 2024 вариант 1

1. Решите уравнение \[ \frac{x+12}{9} - \frac{x-1}{6} = \frac{x+1}{3}. \]
2. Вычислите \[ 3^{24}\bigm/2^{15}\cdot9^{16}. \]
3. Найдите значение выражения \[ (a+1)(a-1)(a^2+1) - (9 + a^2) \] при $a = \tfrac13$.
4. В треугольнике $ABC$ биссектрисы $AK$ и $BM$ пересекаются в точке $O$. Найдите угол $C$ треугольника, если $\angle BOK = 70^\circ$.
   
   
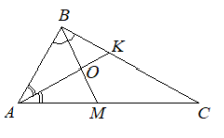
5. При каком значении $k$ график функции $y = kx - 6$ проходит через точку $A(-2;20)$?

1. Сколько различных пятизначных чисел можно записать с помощью цифр 1, 2, 3, 4?
2. Сумма двух чисел равна 77. Найдите эти числа, если $\tfrac23$ первого числа равны $\tfrac45$ второго. В ответе укажите меньшее число.
3. Решите уравнение $|x| + |5| = 6$. В ответе укажите произведение корней.
4. Решите уравнение $x^3 - 4x^2 - 9x + 36 = 0$. В ответе укажите больший корень.
5. В треугольнике $ABC$ $\angle A = 90^\circ$, а внешний угол при вершине $B$ равен $150^\circ$. Найдите $AC$, если $BC - AC = 10$.
6. В школе $40\%$ учащихся имеют плохое зрение. $70\%$ из них носят очки, остальные $30\%$ – пользуются контактными линзами. Общее число ребят в очках – 210. Сколько учащихся в школе?

Решения задач

1. Решите уравнение: $\dfrac{x+12}{9} - \dfrac{x-1}{6} = \dfrac{x+1}{3}$.
   Решение: Умножим обе части уравнения на 18 (НОК знаменателей):
   $2(x+12) - 3(x-1) = 6(x+1)$
   $2x + 24 - 3x + 3 = 6x + 6$
   $-x + 27 = 6x + 6$
   $-7x = -21$
   $x = 3$
   Ответ: 3.
2. Вычислите: $3^{24} \div (2^{15} \cdot 9^{16})$.
   Решение: Упростим выражение:
   $9^{16} = (3^2)^{16} = 3^{32}$
   Тогда $3^{24}/(2^{15} \cdot 3^{32}) = 3^{-8}/2^{15} = \dfrac{1}{2^{15} \cdot 3^8}$.
   Ответ: $\dfrac{1}{2^{15} \cdot 3^8}$.
3. Найдите значение выражения: $(a+1)(a-1)(a^2+1) - (9 + a^2)$ при $a = \dfrac{1}{3}$.
   Решение: Упростим выражение:
   $(a^2 - 1)(a^2 + 1) - (9 + a^2) = a^4 - 1 - 9 - a^2 = a^4 - a^2 - 10$
   Подставим $a = \dfrac{1}{3}$:
   $\left(\dfrac{1}{3}\right)^4 - \left(\dfrac{1}{3}\right)^2 - 10 = \dfrac{1}{81} - \dfrac{1}{9} - 10 = \dfrac{-818}{81}$.
   Ответ: $\dfrac{-818}{81}$.
4. В треугольнике $ABC$ биссектрисы $AK$ и $BM$ пересекаются в точке $O$. Найдите угол $C$, если $\angle BOK = 70^\circ$.
   Решение: Сумма углов треугольника $\angle B + \angle A = 140^\circ$ (из свойства внутренних углов). Внешний угол при вершине $C$ равен $180^\circ - 70^\circ = 110^\circ$. Используя теорему о сумме углов треугольника $\angle C = 180^\circ - (90^\circ + 20^\circ) = 40^\circ$.
   Ответ: $40^\circ$.
5. При каком значении $k$ график функции $y = kx - 6$ проходит через точку $A(-2;20)$?
   Решение: Подставим координаты точки:
   $20 = k(-2) - 6$
   $20 + 6 = -2k$
   $k = \dfrac{26}{-2} = -13$.
   Ответ: $-13$.
6. Сколько различных пятизначных чисел можно записать с помощью цифр 1, 2, 3, 4?
   Решение: Так как цифры могут повторяться, каждая из 5 позиций имеет 4 варианта:
   $4^5 = 1024$.
   Ответ: 1024.
7. Сумма двух чисел равна 77. Найдите эти числа, если $\dfrac{2}{3}$ первого числа равны $\dfrac{4}{5}$ второго. Меньшее число:
   Решение: Пусть первое число $x$, второе $y$:
   $\begin{cases} x + y = 77 \\ \dfrac{2}{3}x = \dfrac{4}{5}y \end{cases}$
   Решив систему, получим $x = 42$, $y = 35$.
   Ответ: 35.
8. Решите уравнение $|x| + |5| = 6$. Произведение корней:
   Решение: $|x| = 1 \Rightarrow x = 1$ или $x = -1$.
   Произведение: $1 \cdot (-1) = -1$.
   Ответ: $-1$.
9. Решите уравнение $x^3 - 4x^2 - 9x + 36 = 0$. Больший корень:
   Решение: Разложим на множители:
   $(x^3 - 4x^2) - (9x - 36) = 0 \Rightarrow (x-4)(x^2-9) = 0 \Rightarrow x = 4, 3, -3$.
   Ответ: 4.
10. В треугольнике $ABC$ $\angle A = 90^\circ$, а внешний угол при вершине $B$ равен $150^\circ$. Найдите $AC$, если $BC - AC = 10$.
    Решение: Внутренний угол $B = 30^\circ$, тогда $AC = BC \cdot \sin(30^\circ) = \dfrac{BC}{2}$. Из условия $BC - \dfrac{BC}{2} = 10 \Rightarrow BC = 20 \Rightarrow AC = 10$.
    Ответ: 10.
11. Общее число ребят в очках — 210. Сколько учащихся в школе?
    Решение: Пусть всего учеников $x$:
    $0.4x \cdot 0.7 = 210 \Rightarrow 0.28x = 210 \Rightarrow x = 750$.
    Ответ: 750.