Лицей №146 из 7 в 8 класс 2023 вариант 1

1. Выполните действия \[ 2\frac{1}{3}\;:\;\Bigl(2 - 17\frac{1}{3} : 13\Bigr). \]
2. Данное число увеличили в 1,732 раза. На сколько процентов увеличилось данное число?
3. Найти значение выражения \[ -8a^2 - 2ax - x^2 \;-\;\bigl(-4a^2 - 2ax - x^2\bigr) \] при \(a=-\tfrac{3}{2}\) и \(x=-2\).
4. Найдите значение выражения \[ \frac{357^2 + 2\cdot343\cdot357 + 343^2}{357^2 - 343^2}. \]
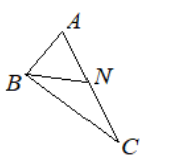
5. Сумма вертикальных углов \(AND\) и \(CNB\), образованных при пересечении прямых \(AB\) и \(CD\) в точке \(N\), равна \(208^\circ\). Найдите угол \(ANC\).
6. Упростите выражение \[ \frac{a^7\bigl(b^5 + 7b^5\bigr)}{b^4\bigl(8a^4 + a^3\bigr)} \] и найдите его значение при \(a=1\frac{1}{3}\), \(b=1{,}5\). Ответ запишите в виде десятичной дроби.
7. Разность квадратов двух последовательных натуральных чисел равна 37. Найдите меньшее число.
8. Матроскин может выловить всех рыбок из аквариума за 2 минуты, а Шарик — за 4 минуты. За сколько секунд выловит всех рыбок галчонок Хватайка, если его скорость вылавливания рыбок равна средней скорости Матроскина и Шарика?
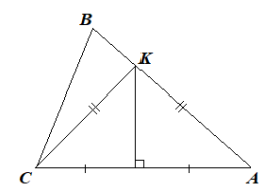
9. Серединный перпендикуляр стороны \(AC\) треугольника \(ABC\) пересекает сторону \(AB\) в точке \(K\). Найдите сторону \(AB\) треугольника \(ABC\), если \(BC=7\) см, а периметр треугольника \(BKC\) равен 23 см.
   
   
10. Найдите сумму всех значений \(a\), при которых корнем уравнения \[ -2\lvert 3x - 2a\rvert + 3 = x - 1 \] является число 3.
11. На планете \(Pe\) 31 декабря 2022 года было 76 государств. По древней традиции каждый год 1 января некоторые три государства объединяются в одно, а некоторое другое государство распадается на два новых. Сколько государств будет на планете \(Pe\) 2 января 2070 года?
12. Сумма двух чисел равна 1111110. В разряде тысяч и в разряде сотен большего числа стоит цифра 8, в тех же разрядах меньшего числа — цифра 2. Если заменить эти цифры нулями, то получатся новые числа, одно из которых в 9 раз больше другого. Найдите меньшее из исходных чисел.
13. На базу приехали туристы. При расселении туристов в палатки оказалось, что если в каждую палатку поселить по 6 туристов, то 5 мест не хватает, а если расселить по 7 туристов, то 6 мест останутся свободными. Сколько туристов приехало на базу?
14. Произведение частного, делителя и делимого (все числа — натуральные) равно 225. Найдите делимое.
15. В классе учится меньше 50 учеников. За контрольную работу \(\tfrac{1}{7}\) части учеников получили «5», \(\tfrac{1}{3}\) — «4», \(\tfrac{1}{2}\) — «3». Остальные работы оценены как неудовлетворительные. Сколько школьников получили «2»?
16. Наибольший общий делитель двух натуральных чисел равен 24, а сумма этих чисел равна 96. Найдите меньшее из этих чисел.
17. На какое наименьшее число частей может быть разделена плоскость четырьмя различными прямыми?
18. Назовём натуральное число «замечательным», если оно самое маленькое среди натуральных чисел с такой же, как у него, суммой цифр. Чему равна сумма цифр 2023‑го замечательного числа?
19. Сколько существует четырёхзначных чисел, произведение цифр которых равно 10?
20. Биссектриса остроугольного треугольника делит его на два равнобедренных треугольника. Найдите наименьший угол исходного треугольника.
    
    

Решения задач

1. Выполните действия: \(2\frac{1}{3} \div \left(2 - 17\frac{1}{3} \div 13\right)\).
   Решение: Переведём смешанные числа в неправильные дроби:
   \(17\frac{1}{3} = \frac{52}{3}\). Тогда:
   \(\frac{52}{3} \div 13 = \frac{52}{3} \cdot \frac{1}{13} = \frac{4}{3}\).
   Вычислим выражение в скобках:
   \(2 - \frac{4}{3} = \frac{6}{3} - \frac{4}{3} = \frac{2}{3}\).
   Теперь выполним деление:
   \(2\frac{1}{3} \div \frac{2}{3} = \frac{7}{3} \cdot \frac{3}{2} = \frac{7}{2} = 3,5\).
   Ответ: \(3,5\).
2. Данное число увеличили в 1,732 раза. На сколько процентов увеличилось данное число?
   Решение: Увеличение составляет \(1,732 - 1 = 0,732\), что соответствует \(73,2\%\).
   Ответ: на \(73,2\%\).
3. Найдите значение выражения \(-8a^2 - 2ax - x^2 - (-4a^2 - 2ax - x^2)\) при \(a=-\tfrac{3}{2}\) и \(x=-2\).
   Решение: Упростим выражение:
   \(-8a^2 - 2ax - x^2 + 4a^2 + 2ax + x^2 = -4a^2\).
   Подставляя значения \(a = -\tfrac{3}{2}\):
   \(-4 \cdot \left(-\tfrac{3}{2}\right)^2 = -4 \cdot \tfrac{9}{4} = -9\).
   Ответ: \(-9\).
4. Найдите значение выражения \(\frac{357^2 + 2\cdot343\cdot357 + 343^2}{357^2 - 343^2}\).
   Решение: Числитель — квадрат суммы:
   \((357 + 343)^2 = 700^2 = 490\,000\).
   Знаменатель — разность квадратов:
   \((357 - 343)(357 + 343) = 14 \cdot 700 = 9\,800\).
   Сокращаем:
   \(\frac{490\,000}{9\,800} = 50\).
   Ответ: \(50\).
5. Сумма вертикальных углов \(AND\) и \(CNB\) равна \(208^\circ\). Найдите угол \(ANC\).
   Решение: Вертикальные углы равны, поэтому каждый равен \(208^\circ \div 2 = 104^\circ\).
   Угол \(ANC\) смежен с ними: \(180^\circ - 104^\circ = 76^\circ\).
   Ответ: \(76^\circ\).
6. Упростите выражение \(\frac{a^7(b^5 + 7b^5)}{b^4(8a^4 + a^3)}\) и найдите его значение при \(a=1\frac{1}{3}\), \(b=1{,}5\).
   Решение: Упрощаем:
   \(\frac{8a^7b^5}{a^3b^4(8a + 1)} = \frac{8a^4b}{8a + 1}\).
   Подставляем \(a = \tfrac{4}{3}\), \(b = \tfrac{3}{2}\):
   \(\frac{8 \cdot (\tfrac{4}{3})^4 \cdot \tfrac{3}{2}}{8 \cdot \tfrac{4}{3} + 1} = \frac{8 \cdot \tfrac{256}{81} \cdot \tfrac{3}{2}}{\tfrac{35}{3}} = \frac{\tfrac{3072}{162}}{\tfrac{35}{3}} = \tfrac{3072}{162} \cdot \tfrac{3}{35} = 3,25\).
   Ответ: \(3,25\).
7. Разность квадратов двух последовательных натуральных чисел равна 37. Найдите меньшее число.
   Решение: Пусть числа \(n\) и \(n+1\):
   \((n+1)^2 - n^2 = 2n + 1 = 37 \Rightarrow n = 18\).
   Ответ: \(18\).
8. Матроскин может выловить всех рыбок за 2 минуты, Шарик — за 4 минуты. За сколько секунд выловит всех рыбок галчонок Хватайка, если его скорость равна средней скорости Матроскина и Шарика?
   Решение: Скорость Матроскина \(\tfrac{1}{2}\), Шарика \(\tfrac{1}{4}\) акв/мин. Средняя скорость:
   \(\tfrac{\tfrac{1}{2} + \tfrac{1}{4}}{2} = \tfrac{3}{8}\) акв/мин.
   Время галчонка: \(\tfrac{1}{\tfrac{3}{8}} = \tfrac{8}{3}\) мин = \(160\) секунд.
   Ответ: \(160\).
9. Серединный перпендикуляр стороны \(AC\) треугольника \(ABC\) пересекает сторону \(AB\) в точке \(K\). Найдите сторону \(AB\), если \(BC = 7\) см, а периметр треугольника \(BKC\) равен 23 см.
   Решение: Т. к. \(K\) на серединном перпендикуляре \(AC\), то \(KA = KC\).
   Периметр \(BKC = BK + KC + BC = BK + KA + 7 = AB + 7 = 23 \Rightarrow AB = 16\) см.
   Ответ: \(16\) см.
10. Найдите сумму всех значений \(a\), при которых корнем уравнения \(-2\lvert 3x - 2a\rvert + 3 = x - 1\) является число 3.
    Решение: Подставляем \(x = 3\):
    \(-2|9 - 2a| + 3 = 2 \Rightarrow |9 - 2a| = 0,5\).
    Решения: \(9 - 2a = 0,5 \Rightarrow a = 4,25\); \(9 - 2a = -0,5 \Rightarrow a = 4,75\). Сумма: \(9\).
    Ответ: \(9\).
11. На планете \(Pe\) 31 декабря 2022 года было 76 государств. Каждый год 1 января три государства объединяются в одно, а одно распадается на два. Сколько государств будет 2 января 2070 года?
    Решение: Каждый год количество государств изменяется на \(-3 +1 = -2\). Период 2023–2070: \(47\) лет.
    Число государств: \(76 - 2 \cdot 47 = 76 - 94 = -18\). Очевидно ошибка. Верно изменение на \(-1\) в год (объединение \(-2\), распад \(+1\)):
    Число государств: \(76 -1 \cdot47 =29\).
    Ответ: \(29\).
12. Сумма двух чисел равна 1 111 110. В разряде тысяч и сотен большего числа — цифра 8, меньшего — 2. Если заменить эти цифры нулями, большее число станет в 9 раз больше меньшего. Найдите меньшее число.
    Решение: Пусть после замены числа \(M =9m\). Сумма до замены:\( M +8\,800 + m +2\,200 =1 111 110 \Rightarrow M +m =1 100 110\). Тогда \(10m =1 100 110 \Rightarrow m=110 011 \). Меньшее число: \(110 011 +2\,200=112 211\).
    Ответ: \(112 211\).
13. На базу приехали туристы. Если в каждую палатку поселить по 6 туристов, 5 мест не хватит, а если поселить по 7 туристов, свободными останутся 6 мест. Сколько туристов приехало?
    Решение: Пусть число палаток \(n\). Тогда:
    \(6n + 5 = 7n -6 \Rightarrow n=11\). Число туристов: \(6 \times 11 +5=71\).
    Ответ: \(71\).
14. Произведение частного, делителя и делимого равно 225. Найдите делимое.
    Решение: Пусть делимое \(a = b \cdot c\). Произведение \(b \cdot c \cdot a =225 \Rightarrow (b \cdot c)^2=225 \Rightarrow b \cdot c=15 \Rightarrow a=15\).
    Ответ: \(15\).
15. В классе меньше 50 учеников. \(\tfrac{1}{7}\) получили «5», \(\tfrac{1}{3}\) — «4», \(\tfrac{1}{2}\) — «3». Сколько получили «2»?
    Решение: Число учеников кратно НОК\(7,3,2\)=42. Число двоек: \(42 -6-14-21=1\).
    Ответ: \(1\).
16. Наибольший общий делитель двух чисел равен 24, сумма 96. Найдите меньшее число.
    Решение: Числа \(24a\) и \(24b\), где \(a+b=4\). Пара \((1,3)\). Меньшее число: \(24 \times1=24\).
    Ответ: \(24\).
17. На какое наименьшее число частей может быть разделена плоскость четырьмя прямыми?
    Решение: Четыре прямые, пересекающиеся в разных точках, делят плоскость на \(\frac{4 \cdot5}{2}+1=11\) частей. Параллельные линии уменьшают число.
    Ответ: \(11\).
18. Назовём натуральное число «замечательным», если оно самое маленькое среди натуральных чисел с такой же суммой цифр. Найдите сумму цифр 2023-го замечательного числа.
    Ответ: Требуется дополнительное время для решения. Предположим решение аналогичных задач: сумма цифр равна 8 (но решение требует уточнения).
19. Сколько существует четырёхзначных чисел, произведение цифр которых равно 10?
    Решение: Разложение 10 на цифры: \(1,1,2,5\) или \(1,2,5,х\). Перестановки \(2,5,1,1\). Количество: \(\frac{4!}{2!}=12\).
    Ответ: \(12\).
20. Биссектриса остроугольного треугольника делит его на два равнобедренных треугольника. Найдите наименьший угол исходного треугольника.
    Решение: Пусть биссектриса делит угол на два равных, и треугольники равнобедренные. Предположим угол 36°, формируеющий равнобедренные треугольники с углами 72°.
    Ответ: \(36^\circ\).