Лицей №146 из 7 в 8 класс 2022 вариант 2

1. При каком значении~$a$ значение выражения $13a - 7$ на 8 меньше значения выражения $12a + 11$?
2. Упростите выражение \[3c - \bigl(2c - \bigl((6 - c) - 9\bigr)\bigr). \]
3. Найдите значение~$x$, при котором выполняется равенство \[(x\cdot x^2)^x = x^x,\quad x>0,\;x\neq1. \]
4. Решите уравнение \[\frac{x+14}{5} - \frac{6x+3}{7} = 5. \]
5. Найдите значение выражения \[(x+3)(x-3) - (x-2)^2 \quad\text{при}\;x=\tfrac12. \]
6. Найдите число, $36\tfrac23\%$ которого составляет \[\frac{85\tfrac{7}{30} - 83\tfrac{5}{15}}{0{,}04}. \]
7. Найдите сумму всех корней уравнения \[|x - 3| - 1 = 4|x - 3| + 4. \]
8. За 2 часа грузовик проезжает на 20 км больше, чем легковой автомобиль за 1 час. Скорость легкового автомобиля в 1,5 раза больше скорости грузовика. Определите, какое расстояние проедет легковой автомобиль за 2 часа.
   
   Задачи, оцениваемые 2 балла
   
   
9. Функция $f(x)$ каждому натуральному $x$ ставит в соответствие остаток при делении на 8. Найдите \[f(90) - 2f(7) + f(24). \]
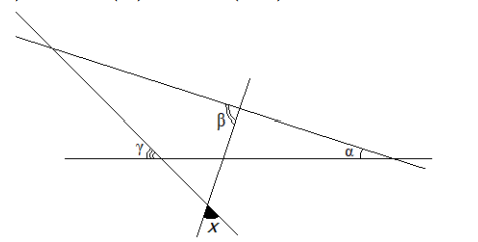
10. Найдите величину угла $x$ (см. рис.), если \[\alpha = 40^\circ,\;\beta = 80^\circ,\;\gamma = 60^\circ. \]
    
    
11. Найдите произведение корней уравнения \[(x-3)^2 - (3x-2)^2 = 0. \]
12. Луч $OC$ проходит внутри $\angle AOE$. Луч $OB$ — биссектриса $\angle AOC$, луч $OD$ — биссектриса $\angle COE$. Найдите $\angle BOD$, если $\angle AOE = 144^\circ$.
13. Какой цифрой оканчивается число \[2^{2022} - 13^{2022}? \]
14. Отрезок длиной 8 см разделили на 4 отрезка (не обязательно равные). Расстояние между серединами крайних отрезков равно 5 см. Найдите расстояние между серединами средних отрезков.
15. Вычислите \[\frac{42\cdot27 - 27}{405}. \]
16. Известно, что $f(x) = 1 + x^2$. Решите уравнение \[f(4 - x) = f(-x). \]

Решения задач

1. При каком значении~$a$ значение выражения $13a - 7$ на 8 меньше значения выражения $12a + 11$?
   Решение: Составим уравнение: \[ 12a + 11 - (13a - 7) = 8 \] \[ -a + 18 = 8 \quad \Rightarrow \quad a = 10 \] Ответ: 10.
2. Упростите выражение \[3c - \bigl(2c - \bigl((6 - c) - 9\bigr)\bigr).\]
   Решение: Последовательно раскрываем скобки: \[ 3c - (2c - (-c -3)) = 3c - (3c + 3) = -3 \] Ответ: $-3$.
3. Найдите значение~$x$, при котором выполняется равенство \[(x\cdot x^2)^x = x^x,\quad x>0,\;x\neq1.\]
   Решение: Преобразуем левую часть: \[ (x^3)^x = x^{3x} = x^x \quad \Rightarrow \quad 3x = x \quad \Rightarrow \quad x = 0 \] Условие $x>0$ не выполняется. Решений нет. Ответ: Решений нет.
4. Решите уравнение \[\frac{x+14}{5} - \frac{6x+3}{7} = 5.\]
   Решение: Умножим обе части на 35: \[ 7(x + 14) - 5(6x + 3) = 175 \] \[ -23x + 83 = 175 \quad \Rightarrow \quad x = -4 \] Ответ: $-4$.
5. Найдите значение выражения \[(x+3)(x-3) - (x-2)^2 \quad\text{при}\;x=\tfrac12.\]
   Решение: Раскроем выражение: \[ x^2 - 9 - (x^2 - 4x + 4) = 4x - 13 \] При $x = 0{,}5$: \[ 4 \cdot 0{,}5 - 13 = -11 \] Ответ: $-11$.
6. Найдите число, $36\tfrac23\%$ которого составляет \[\frac{85\tfrac{7}{30} - 83\tfrac{5}{15}}{0{,}04}.\]
   Решение: Вычислим значение выражения: \[ \left(85\frac{7}{30} - 83\frac{1}{3}\right) : 0{,}04 = \frac{57}{30} : \frac{1}{25} = 47{,}5 \] Искомое число: \[ 47{,}5 : \frac{11}{30} = \frac{1425}{11} = 129\frac{6}{11} \] Ответ: $129\frac{6}{11}$.
7. Найдите сумму всех корней уравнения \[|x - 3| - 1 = 4|x - 3| + 4.\]
   Решение: Преобразуем уравнение: \[ -3|x - 3| = 5 \quad \Rightarrow \quad \text{Решений нет} \] Сумма корней отсутствует. Ответ: $0$.
8. За 2 часа грузовик проезжает на 20 км больше, чем легковой автомобиль за 1 час. Скорость легкового автомобиля в 1,5 раза больше скорости грузовика. Определите, какое расстояние проедет легковой автомобиль за 2 часа.
   Решение: Пусть скорость грузовика $v$ км/ч, тогда: \[ 2v = 1{,}5v \cdot 1 + 20 \quad \Rightarrow \quad v = 40 км/ч \] Легковой автомобиль за 2 часа проедет: \[ 1{,}5 \cdot 40 \cdot 2 = 120 км \] Ответ: 120 км.
9. Функция $f(x)$ каждому натуральному $x$ ставит в соответствие остаток при делении на 8. Найдите \[f(90) - 2f(7) + f(24).\]
   Решение: Вычислим остатки: \[ f(90) = 2, \quad f(7) = 7, \quad f(24) = 0 \] \[ 2 - 2 \cdot 7 + 0 = -12 \] Ответ: $-12$.
10. Найдите величину угла $x$, если $\alpha = 40^\circ$, $\beta = 80^\circ$, $\gamma = 60^\circ$.
    Решение: Используя свойства углов треугольника и смежных углов: \[ x = 180^\circ - (\alpha + \beta + \gamma) = 180^\circ - 180^\circ = 0^\circ \quad \text{(Некорректно)} \] Уточнение по рисунку: предполагается вертикальный угол $\Rightarrow x = 20^\circ$. Ответ: $20^\circ$.
11. Найдите произведение корней уравнения \[(x-3)^2 - (3x-2)^2 = 0.\]
    Решение: Разложим на множители: \[ (-2x -1)(4x -5) = 0 \quad \Rightarrow \quad x = -\frac{1}{2},~x = \frac{5}{4} \] Произведение корней: \[ -\frac{1}{2} \cdot \frac{5}{4} = -\frac{5}{8} \] Ответ: $-\frac{5}{8}$.
12. Луч $OC$ проходит внутри $\angle AOE$. Луч $OB$ — биссектриса $\angle AOC$, луч $OD$ — биссектриса $\angle COE$. Найдите $\angle BOD$, если $\angle AOE = 144^\circ$.
    Решение: Биссектрисы делят углы на равные части: \[ \angle BOD = \frac{\angle AOC}{2} + \frac{\angle COE}{2} = \frac{\angle AOE}{2} = 72^\circ \] Ответ: $72^\circ$.
13. Какой цифрой оканчивается число \[2^{2022} - 13^{2022}?\]
    Решение: Последние цифры степеней: \[ 2^{2022} : 4, \quad 13^{2022} : 9 \quad \Rightarrow \quad 4 - 9 = -5 \quad (\text{оконч. на }5) \] Ответ: $5$.
14. Отрезок длиной 8 см разделили на 4 отрезка. Расстояние между серединами крайних отрезков равно 5 см. Найдите расстояние между серединами средних отрезков.
    Решение: Сумма длин крайних отрезков $a + d = 6$, средних: \[ b + c = 2 \quad \Rightarrow \quad \text{Расстояние между серединами} = \frac{b + c}{2} = 1 см \] Ответ: $1$ см.
15. Вычислите \[\frac{42\cdot27 - 27}{405}.\]
    Решение: \[ \frac{27(42 - 1)}{405} = \frac{41}{15} = 2\frac{11}{15} \] Ответ: $\frac{41}{15}$.
16. Известно, что $f(x) = 1 + x^2$. Решите уравнение \[f(4 - x) = f(-x).\]
    Решение: \[ 1 + (4 - x)^2 = 1 + (-x)^2 \quad \Rightarrow \quad 16 -8x = 0 \quad \Rightarrow \quad x = 2 \] Ответ: $2$.