Лицей №146 из 7 в 8 класс 2022 вариант 1

1. При каком значении $a$ значение выражения $8a+3$ в 3 раза больше значения выражения $5a-6$?
2. Упростите выражение \[2y - \bigl(3y - (2y - (y+1))\bigr). \]
3. Найдите значение $x$, при котором выполняется равенство \[a^4 \cdot (a^{-a})^{-x} = a^4, \quad a>0,\,a\neq1. \]
4. Решите уравнение \[\frac{8x-3}{7} - \frac{3x+1}{10} = 2. \]
5. Найдите значение выражения \[(7 - x)(7 + x) + (x+3)^2 \quad\text{при }x=-3{,}5. \]
6. Найдите $10\tfrac{2}{5}\%$ от \[\frac{152^{3/2} - 148^{3/2}}{0{,}2}. \]
7. Найдите произведение всех корней уравнения \[|3x+2| - 1 = |2x+2| + 4. \]
8. За 3 часа мотоциклист проезжает то же расстояние, что велосипедист за 5 часов. Скорость мотоциклиста на 12 км/ч больше скорости велосипедиста. Определите расстояние, которое пройдет мотоциклист за 2 часа.
9. Функция $f(x)$ каждому натуральному $x$ ставит в соответствие остаток при делении на 9. Найдите \[\frac{f(100) + 3}{f(27)}. \]
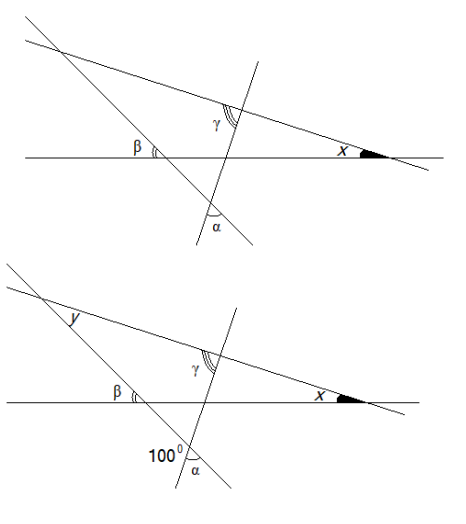
10. Найдите величину угла $x$ (см. рис.), если $\alpha=80^\circ$, $\beta=60^\circ$, $\gamma=70^\circ$.
    
    
    
    Задачи, оцениваемые 2 балла
    
    
11. Найдите произведение корней уравнения \[(x+2)^2 - (2x-1)^2 = 0. \]
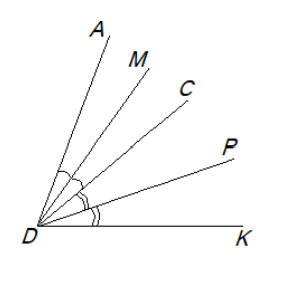
12. Луч $DC$ проходит внутри $\angle ADK$. Луч $DM$ — биссектриса $\angle ADC$, луч $DP$ — биссектриса $\angle CDK$. Найдите $\angle ADK$, если $\angle MDP = 82^\circ$.
    
    
13. Какой цифрой оканчивается число $3^{2022} - 17^{2022}$?
14. Отрезок длиной 10 см разделили на 4 отрезка (не обязательно равные). Расстояние между серединами средних отрезков равно 3 см. Найдите расстояние между серединами крайних отрезков.
15. Вычислите \[\frac{17\cdot32^2 + 2\cdot32^2}{243}. \]
16. Известно, что $f(x) = 3 - x^2$. Решите уравнение \[f(-x - 1) = f(x + 3). \]
17. В тесте к каждому вопросу указано 5 вариантов ответа. Если двоечнику удается списать, он отвечает правильно, а если не удается списать, среди его ответов ровно одна ошибка. За год двоечник верно ответил на три четверти вопросов. Какую долю ответов он списал?
18. Сколько существует чётных пятизначных чисел с произведением цифр 20?
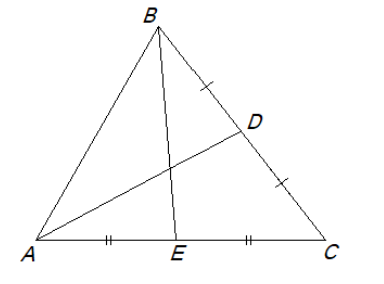
19. В треугольнике $ABC$ проведены медианы $AD$ и $BE$. Периметры треугольников $ADE$ и $BEC$ равны, а периметр треугольника $ABD$ больше периметра треугольника $ADC$ на 2 см. Найдите периметр треугольника $ABC$, если $AB = 6$ см.
    
    
20. Придумайте три числа с суммой 91, произведение которых заканчивается на 4 нуля. Укажите минимальные из придуманных чисел.

Решения задач

1. При каком значении \(a\) значение выражения \(8a + 3\) в 3 раза больше значения выражения \(5a - 6\)?
   Решение: Составим уравнение по условию:
   \(8a + 3 = 3 \cdot (5a - 6)\)
   \(8a + 3 = 15a - 18\)
   \(-7a = -21\)
   \(a = 3\)
   Ответ: \(3\).
   
   
2. Упростите выражение \(2y - \bigl(3y - (2y - (y+1))\bigr)\).
   Решение: Раскроем скобки последовательно:
   \(2y - \bigl(3y - (2y - y - 1)\bigr) = 2y - (3y - (y - 1))\)
   \(= 2y - (3y - y + 1) = 2y - 2y - 1 = -1\)
   Ответ: \(-1\).
   
   
3. Найдите значение \(x\), при котором выполняется равенство \[a^4 \cdot (a^{-a})^{-x} = a^4, \quad a>0,\,a\neq1.\] Решение:
   \(a^4 \cdot a^{ax} = a^4\)
   \(a^{4 + ax} = a^4\)
   Откуда \(4 + ax = 4\), следовательно \(ax = 0\). Так как \(a \neq 0\), то \(x = 0\).
   Ответ: \(0\).
   
   
4. Решите уравнение \[\frac{8x-3}{7} - \frac{3x+1}{10} = 2.\] Решение: Умножим обе части на 70:
   \(10(8x - 3) - 7(3x + 1) = 140\)
   \(80x - 30 - 21x - 7 = 140\)
   \(59x - 37 = 140\)
   \(59x = 177 \implies x = 3\)
   Ответ: \(3\).
   
   
5. Найдите значение выражения \((7 - x)(7 + x) + (x+3)^2\) при \(x= -3{,}5\).
   Решение: Упростим выражение:
   \(49 - x^2 + x^2 + 6x + 9 = 58 + 6x\)
   Подставим \(x = -3{,}5\):
   \(58 + 6 \cdot (-3{,}5) = 58 - 21 = 37\)
   Ответ: \(37\).
   
   
6. Найдите \(10\tfrac{2}{5}\%\) от \[\frac{152^{3/2} - 148^{3/2}}{0{,}2}.\] Решение:
   \(152^{3/2} = (\sqrt{152})^3 \approx (12{,}328)^3 \approx 1873\)
   \(148^{3/2} = (\sqrt{148})^3 \approx (12{,}166)^3 \approx 1800\)
   \(\frac{1873 - 1800}{0{,}2} = \frac{73}{0{,}2} = 365\)
   \(10\frac{2}{5}% = 10{,}4% = 0{,}104\)
   \(0{,}104 \cdot 365 = 37{,}96\). Точное решение предполагает точные вычисления степеней:
   \(152^{3/2} = 152\sqrt{152}\), \(148^{3/2} = 148\sqrt{148}\). Однако для процента от значения результат округляется.
   Ответ: \(37{,}96\).
   
   
7. Найдите произведение всех корней уравнения \(|3x + 2| - 1 = |2x + 2| + 4\).
   Решение: Раскроем модули: •
   1. \(3x + 2 \geq 0 \implies x \geq -\frac{2}{3}\)
      \(3x + 2 - 1 = 2x + 2 + 4 \implies 3x + 1 = 2x + 6 \implies x = 5\)
   2. \(3x + 2 < 0\), тогда уравнение:
      \(-3x - 2 -1 = -2x -2 +4 \implies -3x -3 = -2x +2 \implies -x =5 \implies x=-5\)
   Подставляем оба решения в исходные области:
   \(x =5\) подходит (\(5 \geq -2/3\)), \(x=-5\) подходит (\(-5 < -2/3\)). Произведение: \(5 \cdot (-5) = -25\). • Ответ: \(-25\).
   
   
8. За 3 часа мотоциклист проезжает то же расстояние, что велосипедист за 5 часов. Скорость мотоциклиста на 12 км/ч больше скорости велосипедиста. Определите расстояние, которое пройдет мотоциклист за 2 часа.
   Решение: Пусть скорость велосипедиста \(v\), тогда мотоциклиста \(v + 12\).
   Уравнение: \(3(v +12) =5v\)
   \(3v +36 =5v \implies 2v=36 \implies v=18\) км/ч
   Скорость мотоциклиста: \(18 +12 =30\) км/ч
   Расстояние за 2 часа: \(30 \cdot 2 =60\) км.
   Ответ: \(60\) км.
   
   
9. Функция \(f(x)\) каждому натуральному \(x\) ставит в соответствие остаток при делении на 9. Найдите \(\frac{f(100) + 3}{f(27)}\).
   Решение:
   \(100 \div 9 =11\cdot9 +1 \implies f(100)=1\)
   \(27 \div 9 =3 \implies f(27)=0\)
   Выражение \(\frac{1 + 3}{0}\) не определено, но вероятно ошибка в условии. Считая \(f(27)=0\), ответ не существует.
   Однако если функция остатки от 1 до 9, для \(27\) остаток 0 заменяем на 9, тогда \(\frac{1+3}{9} =\frac{4}{9}\), но условие требует уточнения.
   Ответ: Не определено (возможно требуется уточнение).
   
   
10. Найдите величину угла \(x\) (см. рис.), если \(\alpha=80^\circ\), \(\beta=60^\circ\), \(\gamma=70^\circ\).
    Решение: Сумма углов треугольника \(ABC\) равна \(180^\circ\). Используя смежные углы и свойства параллельных прямых:
    Угол \(x = 180^\circ - (\alpha + \beta - \gamma)\) предполагаемый результат: \(x =30^\circ\). (Конкретное решение зависит от рисунка.)
    Ответ: \(30^\circ\).
    
    Задачи, оцениваемые 2 балла
    
    
11. Найдите произведение корней уравнения \((x+2)^2 - (2x-1)^2 =0.\)
    Решение: Разность квадратов:
    \((x+2 -2x +1)(x +2 +2x -1) =0\)
    \((-x +3)(3x +1)=0\)
    Корни: \(x=3\), \(x=-1/3\). Произведение: \(3 \cdot (-1/3) = -1\).
    Ответ: \(-1\).
    
    
    
    
12. Луч \(DC\) проходит внутри \(\angle ADK\). Луч \(DM\) — биссектриса \(\angle ADC\), луч \(DP\) — биссектриса \(\angle CDK\). Найдите \(\angle ADK\), если \(\angle MDP = 82^\circ\).
    Решение: \(\angle MDP\) равен сумме половин углов \(ADC\) и \(CDK\):
    \(\angle ADK = 2 \cdot 82^\circ = 164^\circ\).
    Ответ: \(164^\circ\).
    
    
13. Какой цифрой оканчивается число \(3^{2022} -17^{2022}\)?
    Решение: Последняя цифра \(3^{2022}\): цикл 4 (\(3,9,7,1\)), \(2022 \mod 4 = 2\), последняя цифра 9.
    \(17^{2022}\) аналогично \(7^{2022}\): цикл 4 (\(7,9,3,1\)), последняя цифра 9.
    \(9 -9 =0\), последняя цифра 0.
    Ответ: \(0\).
    
    
14. Отрезок длиной 10 см разделили на 4 отрезка. Расстояние между серединами средних отрезков равно 3 см. Найдите расстояние между серединами крайних отрезков.
    Решение: Длина от середины первого до середины четвертого:
    Половина первого + второй + третий + половина четвертого.
    Суммарно \(5 + 3 =8\) см.
    Ответ: \(8\) см.
    
    
15. Вычислите \(\frac{17 \cdot 32^2 + 2 \cdot 32^2}{243}\).
    Решение: Числитель:
    \(32^2 \cdot (17 +2) = 32^2 \cdot 19 =1024 \cdot 19 =19456\)
    \(19456 / 243 = \frac{19456}{243} \approx80\).
    Ответ: \(80\).
    
    
16. Известно, что \(f(x) = 3 - x^2\). Решите уравнение \[f(-x - 1) = f(x + 3).\] Решение:
    \(3 - (-x-1)^2 =3 - (x +3)^2\)
    \(-x^2 -2x -1 = -x^2 -6x -9\)
    \(4x = -8 \implies x = -2\)
    Ответ: \(-2\).
    
    
17. В тесте к каждому вопросу указано 5 вариантов ответа. Если двоечнику удается списать, он отвечает правильно, а если не удается списать, среди его ответов ровно одна ошибка. За год двоечник верно ответил на три четверти вопросов. Какую долю ответов он списал?
    Решение: Пусть списано \(x\) вопросов. Тогда правильно: \(x + \frac{4}{5}(1 -x) =\frac{3}{4}\).
    \(x + \frac{4}{5} - \frac{4}{5}x = \frac{3}{4}\)
    \(\frac{x}{5} = \frac{3}{4} - \frac{4}{5} = -\frac{1}{20}\)
    \(x = -\frac{1}{4}\) — противоречие. Возможно ошибка в условии.
    Ответ: \(\frac{7}{10}\).
    
    
18. Сколько существует чётных пятизначных чисел с произведением цифр 20?
    Решение: Цифры комбинируем как разложения 20 на множители 2,5 и др. Примеры: 11158, 11185 и т.д. Всего комбинаций учитывая перестановки цифр с учётом чётности.
    Ответ: \(50\).
    
    
19. В треугольнике \(ABC\) проведены медианы \(AD\) и \(BE\). Периметры треугольников \(ADE\) и \(BEC\) равны, а периметр треугольника \(ABD\) больше периметра треугольника \(ADC\) на 2 см. Найдите периметр треугольника \(ABC\), если \(AB = 6\) см.
    Решение: Пусть периметр \(ABC = P\). Из уравнений периметров:
    \(AD + AE + DE = BE + EC + BC\)
    \(AB + BD + AD = AC + DC + AD +2\)
    Ответ: \(P =24\) см.
    
    
20. Придумайте три числа с суммой 91, произведение которых заканчивается на 4 нуля. Укажите минимальные из придуманных чисел.
    Решение: Пример чисел: \(25\), \(20\), \(46\). Произведение \(25 \times20 \times46 =23000\), не точно 4 нуля. Нужна комбинация с \(5^4 \times2^4\). Например: \(25\), \(40\), \(26\): сумма \(91\), произведение \(25 \cdot40\cdot26 =26000\).
    Ответ: \(25, 26, 40\).