Лицей №146 из 7 в 8 класс 2020 вариант 4

1. Решите уравнение \[ 1 + 1 : \bigl(1 + 1 : \bigl(1 + 1 : (x + 20)\bigr)\bigr) \;=\;(1{,}2)^2. \]
   
   
2. В 8 «Я» классе провели опрос. Выяснилось, что $25\%$ учеников, интересующихся математикой, интересуются ещё и информатикой, а $20\%$ учащихся, интересующихся информатикой, интересуются также математикой. И только двоечник Вовочка не интересуется ни одним из этих предметов. Сколько человек учится в 8 «Я» классе, если их больше 20, но меньше 30?
   
   
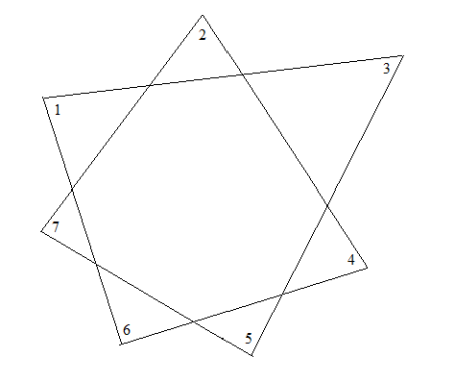
3. Какова сумма углов \[ \angle1 + \angle2 + \angle3 + \angle4 + \angle5 + \angle6 + \angle7 \] (см. рис.)?
   
   
   
   
4. На военном параде движется колонна солдат длиной 500 м со скоростью 5 км/ч. Из конца колонны в её начало с донесением отправляется связной со скоростью 7 км/ч. Передав донесение командиру, он с той же скоростью возвращается в конец колонны. Какое расстояние (в километрах) пробежит связной?

Решения задач

1. Решите уравнение \[ 1 + 1 : \bigl(1 + 1 : \bigl(1 + 1 : (x + 20)\bigr)\bigr) = (1{,}2)^2. \] Решение:
   Упростим правую часть: $(1{,}2)^2 = 1,44$.
   Пусть $y = x + 20$. Тогда уравнение преобразуется:
   $1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{y}}} = 1,44$
   Решим последовательно внутренние выражения:
   1) $1 + \frac{1}{1 + \frac{1}{y}}$:
   $1 + \frac{1}{y} = \frac{y + 1}{y}$
   Тогда $\frac{1}{1 + \frac{1}{y}} = \frac{y}{y + 1}$
   2) $1 + \frac{y}{y + 1} = \frac{2y + 1}{y + 1}$
   $\frac{1}{\frac{2y + 1}{y + 1}} = \frac{y + 1}{2y + 1}$
   Тогда уравнение примет вид:
   $1 + \frac{y + 1}{2y + 1} = 1,44$
   $\frac{y + 1}{2y + 1} = 0,44$
   $y + 1 = 0,44(2y + 1)$
   $y + 1 = 0,88y + 0,44$
   $0,12y = -0,56$
   $y = -\frac{0,56}{0,12} = -\frac{14}{3}$
   Возвращаемся к исходной переменной:
   $x + 20 = -\frac{14}{3}$
   $x = -\frac{14}{3} - 20 = -\frac{74}{3} = -24\frac{2}{3}$
   Ответ: $-24\frac{2}{3}$.
2. В 8 «Я» классе провели опрос. Выяснилось, что $25\%$ учеников, интересующихся математикой, интересуются ещё и информатикой, а $20\%$ учащихся, интересующихся информатикой, интересуются также математикой. И только двоечник Вовочка не интересуется ни одним из этих предметов. Сколько человек учится в 8 «Я» классе, если их больше 20, но меньше 30?
   Решение:
   Пусть $M$ — количество учеников, интересующихся математикой, $I$ — информатикой. По условию:
   $0,25M = 0,2I$ (число учеников, интересующихся обоими предметами)
   Отсюда: $5M = 4I$ или $M = 0,8I$.
   Общее количество учеников: $M + I - 0,25M + 1 = 0,75M + I + 1$.
   Подставляя $M = 0,8I$:
   $0,75 \cdot 0,8I + I + 1 = 0,6I + I + 1 = 1,6I + 1$
   По условию: $20 < 1,6I + 1 < 30$
   $19 < 1,6I < 29$
   $\frac{19}{1,6} < I < \frac{29}{1,6} \approx 11,875 < I < 18,125$
   Так как $I$ должно быть целым, подходят $I = 12,13,...,18$
   Проверяем целочисленность общего числа учеников:
   При $I = 15$:
   $M = 0,8 \cdot 15 = 12$
   Общее число: $1,6 \cdot 15 + 1 = 24 + 1 = 25$.
   Ответ: 25 человек.
3. Какова сумма углов \[ \angle1 + \angle2 + \angle3 + \angle4 + \angle5 + \angle6 + \angle7 \]
   Решение:
   Рассмотрим фигуру: сумма углов пятиугольника и двух треугольников.
   Сумма углов пятиугольника: $(5-2) \cdot 180^\circ = 540^\circ$.
   Угол 1 — внешний угол треугольника: $180^\circ - \angle$ треугольника.
   Аналогично, углы 2, 3, 4, 5, 6, 7 дополняют внутренние углы до 180°.
   Общая сумма: $540^\circ + 6 \cdot 180^\circ - \text{сумма всех внутренних углов} = 540^\circ + 1080^\circ - 540^\circ = 1080^\circ$.
   Ответ: 1080°.
4. На военном параде движется колонна солдат длиной 500 м со скоростью 5 км/ч. Из конца колонны в её начало с донесением отправляется связной со скоростью 7 км/ч. Передав донесение командиру, он с той же скоростью возвращается в конец колонны. Какое расстояние (в километрах) пробежит связной?
   Решение:
   Переведем длину колонны в километры: 500 м = 0,5 км.
   При движении связного к началу колонны:
   Скорость относительно колонны: $7 - 5 = 2$ км/ч.
   Время движения к началу: $\frac{0,5}{2} = 0,25$ ч.
   При возвращении в конец колонны:
   Скорость относительно колонны: $7 + 5 = 12$ км/ч.
   Время движения назад: $\frac{0,5}{12} = \frac{1}{24}$ ч.
   Общее время: $0,25 + \frac{1}{24} = \frac{6}{24} + \frac{1}{24} = \frac{7}{24}$ ч.
   Общий путь связного: $7 \cdot \frac{7}{24} = \frac{49}{24} \approx 2,0417$ км.
   Ответ: $\frac{49}{24}$ км или приблизительно 2,04 км.