Лицей №146 из 7 в 8 класс 2020 вариант 3

1. Решите уравнение \[ 1 + 1 : \bigl(1 + 1 : \bigl(1 + 1 : (x+30)\bigr)\bigr) = (1{,}25)^2. \]
   
   
2. В классе 8 «Я» провели опрос. Выяснилось, что $10\%$ учеников, интересующихся физикой, интересуются ещё и астрономией, а $50\%$ учащихся, интересующихся астрономией, интересуются также и физикой. И только Вася, Петя и Аня не интересуются ни тем, ни другим предметом. Сколько человек учится в 8 «Я» классе, если известно, что их больше 20, но меньше 30?
   
   
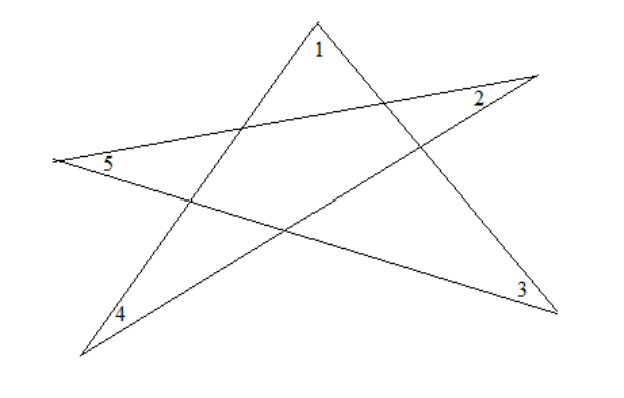
3. Какова сумма углов \[ \angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5 \] (см. рис.)?
   
   
   
   
4. На прогулку вышла колонна туристов длиной 1200 м во главе с Мироном, движущаяся с постоянной скоростью 6 км/ч. Из конца колонны в её начало бежит инструктор Юрий со скоростью 9 км/ч. Передав указания Мирону, Юрий с той же скоростью возвращается назад в конец колонны. Какое расстояние (в километрах) пробежит Юрий?

Решения задач

1. Решите уравнение \[ 1 + 1 : \bigl(1 + 1 : \bigl(1 + 1 : (x+30)\bigr)\bigr) = (1{,}25)^2. \]
   Решение: Упростим правую часть: \[ (1{,}25)^2 = \left(\frac{5}{4}\right)^2 = \frac{25}{16} = 1{,}5625 \] Введём замену для внутреннего выражения: \[ y = 1 + \frac{1}{x+30} \] Тогда уравнение примет вид: \[ 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{y}}} = 1{,}5625 \] Пошагово упрощаем: \[ 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{y}}} = \frac{25}{16} \Rightarrow \frac{1}{1 + \frac{1}{1 + \frac{1}{y}}} = \frac{9}{16} \] Решаем пропорцию: \[ 1 + \frac{1}{1 + \frac{1}{y}} = \frac{16}{9} \Rightarrow \frac{1}{1 + \frac{1}{y}} = \frac{7}{9} \] Далее: \[ 1 + \frac{1}{y} = \frac{9}{7} \Rightarrow \frac{1}{y} = \frac{2}{7} \Rightarrow y = \frac{7}{2} \] Возвращаемся к исходной замене: \[ 1 + \frac{1}{x+30} = \frac{7}{2} \Rightarrow \frac{1}{x+30} = \frac{5}{2} \Rightarrow x + 30 = \frac{2}{5} \Rightarrow x = -\frac{148}{5} = -29{,}6 \] Ответ: -29,6.
2. В классе 8 «Я» провели опрос. Выяснилось, что $10\%$ учеников, интересующихся физикой, интересуются ещё и астрономией, а $50\%$ учащихся, интересующихся астрономией, интересуются также и физикой. И только Вася, Петя и Аня не интересуются ни тем, ни другим предметом. Сколько человек учится в 8 «Я» классе, если известно, что их больше 20, но меньше 30?
   Решение: Пусть количество интересующихся физикой — \( F \), астрономией — \( A \). Согласно условию: \[ 0{,}1F = 0{,}5A \Rightarrow F = 5A \] Общее количество увлечённых: \[ F + A - 0{,}1F = 5A + A - 0{,}5A = 5{,}5A \] Всего учеников: \[ 5{,}5A + 3 \] Так как \( 20 < 5{,}5A + 3 < 30 \), возможные значения: \[ A = 4 \Rightarrow 5{,}5·4 + 3 = 25 \quad \text{(подходит)} \] Ответ: 25 человек.
3. Какова сумма углов \[ \angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5 \] (см. рис.)?
   Решение: Рассмотрим треугольники, образованные звёздой. Сумма углов пятиконечной звезды равна \( 180^\circ \): \[ \angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5 = 180^\circ \] Ответ: \( 180^\circ \).
4. На прогулку вышла колонна туристов длиной 1200 м во главе с Мироном, движущаяся с постоянной скоростью 6 км/ч. Из конца колонны в её начало бежит инструктор Юрий со скоростью 9 км/ч. Передав указания Мирону, Юрий с той же скоростью возвращается назад в конец колонны. Какое расстояние (в километрах) пробежит Юрий?
   Решение:
   1. Относительная скорость Юрия при движении к началу колонны: \[ v_1 = 9 + 6 = 15 \text{ км/ч} \] Время встречи с Мироном: \[ t_1 = \frac{1{,}2}{15} = 0{,}08 \text{ ч} \]
   2. Относительная скорость при возвращении: \[ v_2 = 9 - 6 = 3 \text{ км/ч} \] Время возвращения: \[ t_2 = \frac{1{,}2}{3} = 0{,}4 \text{ ч} \]
   3. Общий путь Юрия: \[ S = 9 · (0{,}08 + 0{,}4) = 9 · 0{,}48 = 4{,}32 \text{ км} \]
   Ответ: 4,32 км.