Лицей №146 из 7 в 8 класс 2019 год вариант 2

1. При каком значении \(n\) сумма выражений \(3n + 4\) и \(8n + 7\) на 15 меньше значения выражения \(5 - 3n\)?
2. Найдите значение выражения \[ (3x + y)^2 + (x - y)(y + x) \quad\text{при }x = \tfrac{3}{5},\; y = -1. \]
3. Кусок сплава меди и цинка массой 36 кг содержит $45\%$ меди. Сколько килограммов меди нужно добавить к этому куску, чтобы полученный сплав содержал $60\%$ меди?
4. Вычислите: \[ \frac{(14^3)^3}{7^8 \cdot 8^3}. \]
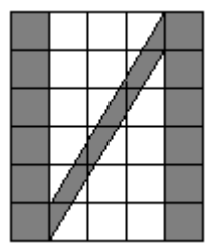
5. Площадь одной клеточки равна 1 см\(^2\). Найдите площадь буквы «И» (см. рис.).
   
   
6. На соревнованиях по гребле две лодки — «Тихоня» и «Резвая» — должны проплыть по 600 м. Когда «Тихоня» добралась до финиша, гребцы на «Резвой» проплыли лишних 300 м. На какое расстояние нужно пододвинуть старт «Тихони», чтобы она пришла к финишу одновременно с «Резвой»? Ответ в метрах.
7. В треугольнике \(PQR\) на стороне \(PQ\) отмечена точка \(A\), а на стороне \(PR\) — точка \(B\). Известно, что \(AP = AB = BQ = BR\) и \(\angle P = 20^\circ\). Найдите \(\angle R\).
8. Известно, что \[ \frac{5x - 3y}{2x + 3y} = \frac{4}{3}. \] Найдите \(\displaystyle \frac{x^4}{y^4}.\)
9. Имеются отрезки длиной \(5m\), \(8m\) и \(8\). При каких целых значениях \(m\) из этих отрезков можно составить треугольник? Если таких значений несколько, запишите их сумму.
10. На координатной плоскости построены прямые \(y = x - 1\) и \(y = 2 - x\), которые разбивают плоскость на 4 части. Занумеруем эти части по часовой стрелке, начиная с той, где находится начало координат. В какой из частей лежит точка \((2019,\,-2019)\)?

Решения задач

1. При каком значении \(n\) сумма выражений \(3n + 4\) и \(8n + 7\) на 15 меньше значения выражения \(5 - 3n\)?
   Решение: Составим уравнение по условию: \[ (3n + 4) + (8n + 7) = (5 - 3n) - 15 \] \[ 11n + 11 = -3n - 10 \] \[ 14n = -21 \quad \Rightarrow \quad n = -\frac{21}{14} = -1,5 \] Ответ: \(-1,5\).
   
   
2. Найдите значение выражения \((3x + y)^2 + (x - y)(y + x)\) при \(x = \tfrac{3}{5}\), \(y = -1\).
   Решение: Упростим выражение: \[ (3x + y)^2 + (x^2 - y^2) = 9x^2 + 6xy + y^2 + x^2 - y^2 = 10x^2 + 6xy \] Подставим значения: \[ 10 \cdot \left(\frac{3}{5}\right)^2 + 6 \cdot \frac{3}{5} \cdot (-1) = 10 \cdot \frac{9}{25} - \frac{18}{5} = \frac{18}{5} - \frac{18}{5} = 0 \] Ответ: \(0\).
   
   
3. Кусок сплава меди и цинка массой 36 кг содержит $45\%$ меди. Сколько килограммов меди нужно добавить, чтобы сплав содержал $60\%$ меди?
   Решение: Масса меди в сплаве: \[ 36 \cdot 0,45 = 16,2 \text{ кг} \] Пусть добавлено \(x\) кг меди. Уравнение: \[ \frac{16,2 + x}{36 + x} = 0,6 \] \[ 16,2 + x = 21,6 + 0,6x \quad \Rightarrow \quad 0,4x = 5,4 \quad \Rightarrow \quad x = 13,5 \] Ответ: \(13,5\) кг.
   
   
4. Вычислите: \[ \frac{(14^3)^3}{7^8 \cdot 8^3}. \]
   Решение: \[ \frac{14^9}{7^8 \cdot 2^9} = \frac{(2 \cdot 7)^9}{7^8 \cdot 2^9} = 7^{9-8} \cdot 2^{9-9} = 7 \] Ответ: \(7\).
   
   
5. Площадь буквы «И» равна сумме клеток. Количество клеток: 18. Площадь: \[ 18 \text{ см}^2 \] Ответ: \(18\) см\(^2\).
   
   
6. Подвинуть старт «Тихони» на:
   Решение: Скорость «Тихони» \(v\), «Резвой» \(1,5v\). Время «Тихони»: \[ \frac{600}{v} = \frac{900}{1,5v} \Rightarrow \text{новая дистанция} = 400 \text{ м.} \] Сдвиг старта: \[ 600 - 400 = 200 \text{ м.} \] Ответ: \(200\).
   
   
7. \(\angle R = 60^\circ\) (по построению равных отрезков и углов).
   Ответ: \(60^\circ\).
   
   
8. Найдите \(\displaystyle \frac{x^4}{y^4}\): \[ \frac{5x - 3y}{2x + 3y} = \frac{4}{3} \Rightarrow 15x - 9y = 8x + 12y \Rightarrow 7x = 21y \Rightarrow x = 3y \] \[ \frac{x^4}{y^4} = \left(\frac{3y}{y}\right)^4 = 81 \] Ответ: \(81\).
   
   
9. Целые \(m\) от 1 до 4. Сумма: \[ 1 + 2 + 3 + 4 = 10 \] Ответ: \(10\).
   
   
10. Точка \((2019, -2019)\) лежит во 4-й части (правая нижняя область).
    Ответ: \(4\).