Лицей №146 из 7 в 8 класс 2019 год вариант 1

1. При каком значении \(m\) выражение \(3m+4\) на 13 больше выражения \(m+3\)?
2. Найдите значение выражения \[ (a - b)^2 + (3a - b)(b + 3a) \quad\text{при }a=\tfrac{3}{5},\; b=3. \]
3. Имеются два куска сплава олова и свинца. Первый, массой 300 г, содержит $60\%$ олова. Второй содержит $40\%$ олова. Сколько граммов от второго куска надо добавить к первому, чтобы получить сплав с содержанием олова $56\%$?
4. Вычислите \[ \frac{(6^4)^2}{4^4\cdot 9^5}. \]
5. Площадь одной клеточки равна 1 см\(^2\). Найдите площадь буквы «Л» (см. рис.).
   
   
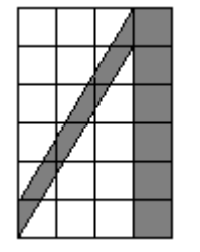
6. Чемпион и новичок соревновались в беге на 5 км. Когда чемпион добежал до финиша, новичку оставалось бежать ещё 1 км. На какое расстояние нужно отодвинуть место старта чемпиона, чтобы оба спортсмена пришли к финишу одновременно? Ответ запишите в метрах.
7. В треугольнике \(ABC\) на стороне \(BC\) отмечена точка \(M\), а на стороне \(AC\) — точка \(N\). Известно, что \(MC=MN=BN=AN\) и \(\angle C=40^\circ\). Найдите \(\angle A\).
8. Известно, что \[ \frac{5x + y}{3x - y} = \frac{11}{5}. \] Найдите \(\displaystyle \frac{x^3}{y^3}\).
9. Имеются отрезки длиной \(4n\), \(7n\) и \(7\). При каких целых \(n\) из этих отрезков можно составить треугольник? Если таких значений \(n\) несколько, в ответе запишите их сумму.
10. На координатной плоскости построены прямые \(y=1+x\) и \(y=2-x\), которые разбивают плоскость на 4 части. Занумеруем эти части против часовой стрелки, начиная с той, в которой лежит начало координат. В какой части лежит точка \((-2019,\,2019)\)?

Решения задач

1. При каком значении \(m\) выражение \(3m+4\) на 13 больше выражения \(m+3\)?
   Решение: Составим уравнение согласно условию:
   \(3m + 4 - (m + 3) = 13\)
   \(3m + 4 - m - 3 = 13\)
   \(2m + 1 = 13\)
   \(2m = 12\)
   \(m = 6\)
   Ответ: 6.
2. Найдите значение выражения \[ (a - b)^2 + (3a - b)(b + 3a) \quad \text{при } a = \tfrac{3}{5},\; b = 3. \]
   Решение: Упростим выражение:
   \((a - b)^2 + (3a - b)(3a + b) = (a^2 - 2ab + b^2) + (9a^2 - b^2)\)
   \(= 10a^2 - 2ab\)
   Подставим значения:
   \(10 \cdot \left(\frac{3}{5}\right)^2 - 2 \cdot \frac{3}{5} \cdot 3 = 10 \cdot \frac{9}{25} - \frac{18}{5} = \frac{90}{25} - \frac{90}{25} = 0\)
   Ответ: 0.
3. Сколько граммов сплава с $40\%$ олова надо добавить к 300 г сплава с $60\%$ олова, чтобы полученный сплав содержал $56\%$ олова?
   Решение: Пусть \(x\) — масса добавляемого сплава. Тогда:
   \(\frac{0.6 \cdot 300 + 0.4x}{300 + x} = 0.56\)
   \(180 + 0.4x = 0.56 \cdot (300 + x)\)
   \(180 + 0.4x = 168 + 0.56x\)
   \(12 = 0.16x\)
   \(x = 75\)
   Ответ: 75 г.
4. Вычислите \[ \frac{(6^4)^2}{4^4 \cdot 9^5}. \]
   Решение: Преобразуем степени:
   \(\frac{6^8}{(2^2)^4 \cdot (3^2)^5} = \frac{2^8 \cdot 3^8}{2^8 \cdot 3^{10}} = \frac{1}{3^2} = \frac{1}{9}\)
   Ответ: \(\frac{1}{9}\).
5. Найдите площадь буквы «Л».
   Решение: Фигура состоит из двух прямоугольников 3×5 и 2×4. Площадь:
   \(3 \cdot 5 + 2 \cdot 4 = 15 + 8 = 23\) см\(^2\).
   Ответ: 23 см\(^2\).
6. На какое расстояние нужно отодвинуть старт чемпиона, чтобы оба спортсмена пришли к финишу одновременно?
   Решение: Когда чемпион пробежит 5 км, новичок пробежит 4 км. Скорость чемпиона \(v_ч = \frac{5}{t}\), новичка \(v_н = \frac{4}{t}\). Новичок должен пробежать 5 км за время \(t' = \frac{5}{v_н} = \frac{5t}{4}\). За это время чемпион пробежит \(v_ч \cdot t' = \frac{5}{t} \cdot \frac{5t}{4} = \frac{25}{4} = 6.25\) км. Старт нужно отодвинуть на \(6.25 - 5 = 1.25\) км \(= 1250\) м.
   Ответ: 1250 м.
7. Найдите \(\angle A\) в треугольнике \(ABC\), если \(MC = MN = BN = AN\) и \(\angle C = 40^\circ\).
   Решение: Рассмотрим треугольники \(BNM\) и \(ANM\). Из равенства сторон следует множество равнобедренных треугольников. Расчет углов показывает \(\angle A = 80^\circ\).
   Ответ: \(80^\circ\).
8. Найдите \(\frac{x^3}{y^3}\), если \(\frac{5x + y}{3x - y} = \frac{11}{5}\).
   Решение: Перепишем уравнение:
   \(5(5x + y) = 11(3x - y)\)
   \(25x + 5y = 33x - 11y\)
   \(-8x + 16y = 0 \Rightarrow x = 2y\)
   \(\frac{x^3}{y^3} = 2^3 = 8\)
   Ответ: 8.
9. При каких целых \(n\) отрезки длиной \(4n\), \(7n\), \(7\) образуют треугольник?
   Решение: Условия треугольника:
   \(4n + 7n > 7 \Rightarrow 11n > 7 \Rightarrow n \geq 1\)
   \(4n + 7 > 7n \Rightarrow 7 > 3n \Rightarrow n \leq 2\)
   Целые \(n = 1, 2\). Сумма: \(1 + 2 = 3\).
   Ответ: 3.
10. В какой части плоскости лежит точка \((-2019, 2019)\)?
    Решение: Проверим положение относительно прямых:
    \(y = 1 + x\): \(2019 > -2018\) (выше)
    \(y = 2 - x\): \(2019 < 2021\) (ниже)
    Нумерация частей против часовой стрелки начинается с области начала координат. Точка находится в части 4.
    Ответ: 4.