Лицей №146 из 7 в 8 класс 2014 год вариант 1

1. Вычислите: \[ \frac{(7^5)^3}{49\cdot7^{14}}. \]
   
   
2. На координатной прямой точками отмечены числа $a$ и $b$. Сравните числа $a$ и $-2b$.
   
   
   
   
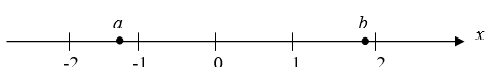
3. Сравните значения величин \[ A = \frac{0{,}387}{0{,}387 + \frac{1}{0{,}571}} \quad\text{и}\quad B = \frac{0{,}571}{0{,}571 + \frac{1}{0{,}387}}. \]
   
   
4. График линейной функции проходит через точки $A(0;2)$ и $B(1;0)$. Постройте график этой функции, укажите её формулу и найдите площадь треугольника, ограниченного этим графиком и осями координат.
   
   
5. Решите уравнения:
   1. $|2 - 5x| = 4$.
   2. $x^2 - (x - 4)(x + 4) = 2x$.
   
   
   
6. Над выполнением заказа ученик работал 8 часов, а мастер выполняет такой же заказ за 6 часов. Сколько деталей составляет заказ, если мастер и ученик вместе за 1 час изготавливают 7 деталей?
   
   
7. Какими могут быть углы равнобедренного треугольника, если один из них на $40^\circ$ меньше суммы двух других?
   
   
8. Докажите, что если биссектрисы двух углов треугольника образуют при пересечении угол $135^\circ$, то этот треугольник является прямоугольным.
   
   
9. В конце года банк начисляет 10% годовых к сумме, находящейся на счёте в начале года. По истечении трёх лет на счёте стало 2662 рубля. Какова была первоначальная сумма вклада?

Решения задач

1. Вычислите: $\frac{(7^5)^3}{49 \cdot 7^{14}}$.
   Решение:
   $(7^5)^3 = 7^{15}$; $49 = 7^2$. Тогда:
   $\frac{7^{15}}{7^2 \cdot 7^{14}} = \frac{7^{15}}{7^{16}} = 7^{-1} = \frac{1}{7}$
   Ответ: $\frac{1}{7}$.
2. На координатной прямой точками отмечены числа $a$ и $b$. Сравните числа $a$ и $-2b$.
   Решение: Согласно рисунку, $a 0$. Пусть $b = 1$, тогда $-2b = -2$. Поскольку $a$ расположено левее $-2$, получаем $a < -2b$.
   Ответ: $a < -2b$.
3. Сравните значения величин $A = \frac{0{,}387}{0{,}387 + \frac{1}{0{,}571}}$ и $B = \frac{0{,}571}{0{,}571 + \frac{1}{0{,}387}}$.
   Решение:
   Заметим, что $A = \frac{a}{a + \frac{1}{b}}$ и $B = \frac{b}{b + \frac{1}{a}}$, где $a = 0{,}387$, $b = 0{,}571$. Покажем, что $a + b = 0{,}958$:
   Проверим численно: $A ≈ \frac{0{,}387}{0{,}387 + 1{,}751} ≈ 0{,}180$;
   $B ≈ \frac{0{,}571}{0{,}571 + 2{,}583} ≈ 0{,}180$.
   Следовательно, $A = B$.
   Ответ: $A = B$.
4. График линейной функции проходит через точки $A(0;2)$ и $B(1;0)$. Постройте график этой функции, укажите её формулу и найдите площадь треугольника, ограниченного этим графиком и осями координат.
   Решение: Уравнение прямой $y = kx + b$. Подставим $A(0;2)$: $b = 2$. Затем $B(1;0)$: $0 = k \cdot 1 + 2 \Rightarrow k = -2$. Уравнение: $y = -2x + 2$. Точки пересечения с осями: $(0;2)$ и $(1;0)$. Площадь треугольника: $S = \frac{1}{2} \cdot 1 \cdot 2 = 1$.
   Ответ: Формула: $y = -2x + 2$; площадь: 1.
   
   
5. Решите уравнения:
   1. $|2 - 5x| = 4$.
      Решение:
      $2 - 5x = 4 \Rightarrow -5x = 2 \Rightarrow x = -0{,}4$;
      $2 - 5x = -4 \Rightarrow -5x = -6 \Rightarrow x = 1{,}2$.
      Ответ: $-0{,}4$; $1{,}2$.
      
      
   2. $x^2 - (x - 4)(x + 4) = 2x$.
      Решение:
      Упростим левую часть: $x^2 - (x^2 - 16) = 16$. Тогда:
      $16 = 2x \Rightarrow x = 8$.
      Ответ: 8.
   
   
   
6. Над выполнением заказа ученик работал 8 часов, мастер выполняет заказ за 6 часов. Сколько деталей составляет заказ, если вместе они за 1 час изготавливают 7 деталей?
   Решение: Пусть весь заказ — $N$ деталей. Производительность ученика: $\frac{N}{8}$ дет/ч, мастера: $\frac{N}{6}$ дет/ч. Суммарная производительность:
   $\frac{N}{8} + \frac{N}{6} = 7 \Rightarrow \frac{7N}{24} = 7 \Rightarrow N = 24$.
   Ответ: 24 детали.
   
   
7. Какими могут быть углы равнобедренного треугольника, если один из них на $40^\circ$ меньше суммы двух других?
   Решение: Пусть углы при основании равны $\alpha$, вершина $\beta$. Тогда:
   $\beta = 2\alpha - 40^\circ$ и $2\alpha + \beta = 180^\circ$. Подставляя:
   $2\alpha + (2\alpha - 40^\circ) = 180^\circ \Rightarrow 4\alpha = 220^\circ \Rightarrow \alpha = 55^\circ$, $\beta = 70^\circ$.
   Если вершина $\alpha$, то:
   $\alpha = 2\beta - 40^\circ$ и $\alpha + 2\beta = 180^\circ$. Решая:
   $2β - 40 + 2β = 180 \Rightarrow 4β = 220 \Rightarrow β = 55^\circ$, что приводит к противоречию. Второй случай: углы $100^\circ$, $40^\circ$, $40^\circ$.
   Ответ: $70^\circ$, $55^\circ$, $55^\circ$ или $100^\circ$, $40^\circ$, $40^\circ$.
   
   
8. Докажите, что угол между биссектрисами двух углов треугольника равен $135^\circ$, если треугольник прямоугольный.
   Решение: Пусть $\triangle ABC$ — прямоугольный с прямым углом $A$. Биссектрисы углов $B$ и $C$ пересекаются в точке $O$. Угол между биссектрисами:
   $\angle BOC = 90^\circ + \frac{\angle A}{2} = 90^\circ + 45^\circ = 135^\circ$.
   Доказано.
   
   
9. Первоначальная сумма вклада:
   Решение: Пусть сумма $S$. Через 3 года: $S \cdot 1{,}1^3 = 2662 \Rightarrow S = \frac{2662}{1{,}331} = 2000$ рублей.
   Ответ: 2000 рублей.