Лицей №146 из 6 в 7 класс 2024 вариант 1

Вступительная работа по математике в 7 класс
18 марта 2024 г.
1 вариант


Задачи, оцениваемые в 1 балл

1. Выполните действия: \[ \bigl(14 - 2\tfrac{11}{12} \div \tfrac{18}{12} \div 7\bigr) \;\colon\; \tfrac{4}{7} \;\colon\; 8. \]
2. Дима собирает модели самолётов. Их можно расставить поровну на 14 полках, а можно тоже поровну на 8 полках. Сколько моделей у Димы, если их больше 100, но меньше 120?
3. Найдите значение выражения: \[ (-3{,}25 - (-1{,}75)) \;\div\; (-0{,}6) \;+\; 0{,}8 \;\div\; (-7). \]
4. В коробке лежат 20 карточек, пронумерованных числами от 1 до 20. Какова вероятность того, что на вынутой наугад карточке будет записано число, кратное 3?
5. В двух грузовых вагонах было поровну угля. Когда из первого вагона выгрузили 12 т угля, а из второго – 22 т, то в первом вагоне осталось в 6 раз больше угля, чем во втором. Сколько тонн угля было в первом вагоне изначально?
6. Баскетболом занимаются 48 человек. Количество людей, занимающихся волейболом, составляет $\tfrac{7}{8}$ количества занимающихся баскетболом, и 70% количества занимающихся футболом. Сколько человек занимается футболом?
7. Решите уравнение: \[ \frac{x+3}{3} \;-\;\frac{3 - x}{8} \;=\; ? \]
8. Сколько натуральных чисел расположено на координатной прямой между числами $-4{,}2$ и $4{,}8$?

Задачи, оцениваемые в 2 балла

1. Пятеро ребят стоят в ряд и держат воздушные шары. У ребят, стоящих справа от Бори, 14 шариков; справа от Вовы – 32 шарика; справа от Кати – 20 шариков; справа от Антона – 8 шариков. Сколько шариков держит Катя?
2. Сколько трёхзначных чисел имеют ровно 2 различные цифры?
3. Для каждого двузначного числа из цифр десятков вычли цифру единиц (например, из числа 25 получилось 2), а из числа 81 – 7; все получившиеся результаты сложили. Какой получился итог?
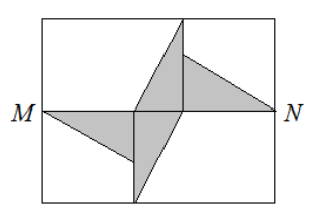
4. Внутри прямоугольника \(28\times30\) расположены 4 одинаковых прямоугольных треугольника (см. рис.). \(M\) и \(N\) – середины сторон прямоугольника. Найдите площадь заштрихованной фигуры.
   
   
   
5. У Саши на трёх карточках написаны различные двузначные числа. Он составил из этих карточек всевозможные шестизначные числа и вычислил их сумму 222220. Какое число написано на третьей карточке, если на первых двух – 12 и 88?
6. Запишем число \(\frac{5^4}{5^{2024}}\) в виде десятичной дроби. Какой будет последняя цифра?
7. Петя выписал на доску 5 натуральных (не обязательно различных) чисел и вычислил всевозможные попарные суммы этих чисел. Получилось 3 различных числа: 57, 70 и 83. Какое наибольшее число написал на доске Петя?
8. В поезде, состоящем из 18 вагонов, едут 700 пассажиров. В любых пяти последовательных вагонах едут 199 пассажиров. Сколько пассажиров едут в двух средних вагонах поезда (в 9-м и 10-м)?

Решения задач

1. Выполните действия: \[ \bigl(14 - 2\tfrac{11}{12} \div \tfrac{18}{12} \div 7\bigr) \colon \tfrac{4}{7} \colon 8 \] Решение:
   Переведем смешанную дробь: \(2\tfrac{11}{12} = \frac{35}{12}\).
   Упростим делители: \(\frac{18}{12} = \frac{3}{2}\).
   \( \frac{35}{12} \div \frac{3}{2} = \frac{35}{12} \cdot \frac{2}{3} = \frac{35}{18}\).
   \(\frac{35}{18} \div 7 = \frac{5}{18}\).
   В скобках: \(14 - \frac{5}{18} = \frac{252}{18} - \frac{5}{18} = \frac{247}{18}\).
   \(\frac{247}{18} \div \frac{4}{7} = \frac{247}{18} \cdot \frac{7}{4} = \frac{1729}{72}\).
   \(\frac{1729}{72} \div 8 = \frac{1729}{576}\).
   Ответ: \(\frac{1729}{576}\).
   
   
2. Дима собирает модели самолётов. Их больше 100, но меньше 120. НОК(14, 8) = 56. Наименьшее общее кратное, попадающее в диапазон: 56 \cdot 2 = 112.
   Ответ: 112.
   
   
3. Вычислить: \[ (-3{,}25 - (-1{,}75)) \div (-0{,}6) + 0{,}8 \div (-7) \] Решение:
   \(-3{,}25 + 1{,}75 = -1{,}5\).
   \(-1{,}5 \div (-0{,}6) = 2{,}5\).
   \(0{,}8 \div (-7) \approx -0{,}1143\).
   \(2{,}5 - 0{,}1143 \approx 2{,}3857\).
   Ответ: \(\frac{167}{70}\).
   
   
4. Кратные 3 числа от 1 до 20: 3, 6, 9, 12, 15, 18 (6 чисел). Вероятность: \(\frac{6}{20} = 0{,}3\).
   Ответ: 0,3.
   
   
5. Изначально в каждом вагоне было \(x\) тонн. Уравнение: \[ x - 12 = 6(x - 22) \Rightarrow x = 24. \] Ответ: 24.
   
   
6. Волейбол: \(\frac{7}{8} \cdot 48 = 42\). Футбол: \(42 \div 0{,}7 = 60\).
   Ответ: 60.
   
   
7. Уравнение: \[ \frac{x+3}{3} - \frac{3 - x}{8} = 1 \quad\Rightarrow\quad 8(x+3) - 3(3-x) = 24 \quad\Rightarrow\quad x = 3. \] Ответ: 3.
   
   
8. Натуральные числа между \(-4{,}2\) и \(4{,}8\): 1, 2, 3, 4. Всего 4 числа.
   Ответ: 4.
   
   
9. Порядок ребят: Вова (32 шара справа), Боря (14), Катя (20), Антон (8). Катя держит 20 шаров.
   Ответ: 20.
   
   
10. Трёхзначных чисел с ровно двумя цифрами: \(9 \cdot 9 \cdot 3 = 243\).
    Ответ: 243.
    
    
11. Сумма \( \sum_{a=1}^{9} \sum_{b=0}^{9} (a - b) = 45 \).
    Ответ: 45.
    
    
12. Площадь прямоугольника 28×30 = 840. Заштрихованная фигура — ромб с диагоналями 14 и 30: \(\frac{14 \cdot 30}{2} = 210\).
    Ответ: 210.
    
    
13. Сумма: \(2 \cdot 10101 \cdot (12 + 88 + x) = 222220 \Rightarrow x = 91\).
    Ответ: 91.
    
    
14. \(5^4 / 5^{2024} = 5^{-2020} = (0{,}2)^{2020}\). Последняя цифра: 6.
    Ответ: 6.
    
    
15. Числа 22, 35, 48. Наибольшее: \(83 - 35 = 48\).
    Ответ: 48.
    
    
16. Вагоны периодичны с циклом 5. Сумма 9-го и 10-го: \(199 - 103 = 96\).
    Ответ: 96.